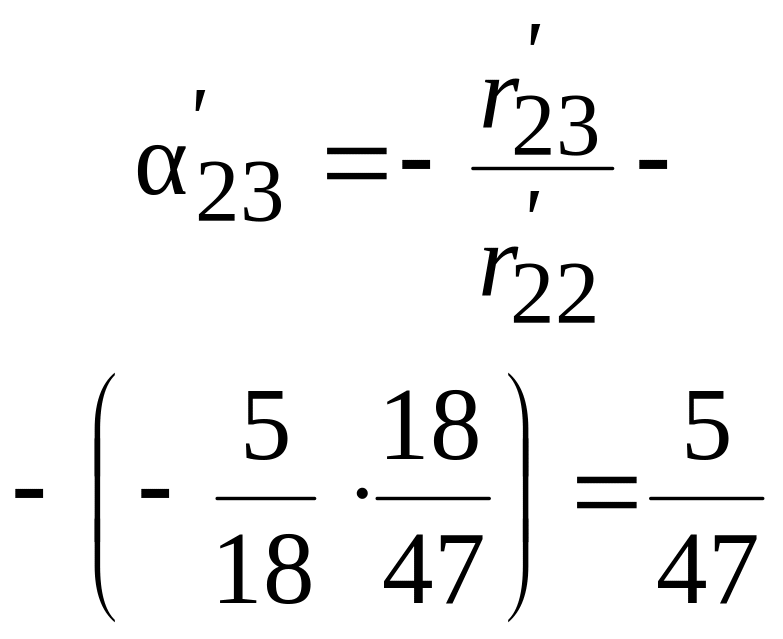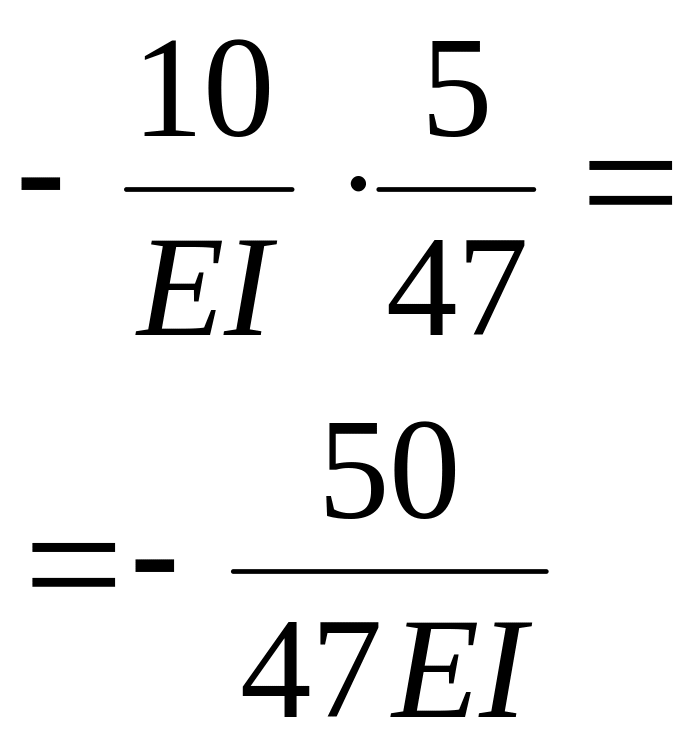2.7 Розв’язання системи канонічних рівнянь та визначення невідомих методу переміщень

Після перевірки підставимо визначені коефіцієнти та вільні члени в систему канонічних рівнянь, яка буде мати такий вигляд:

;

;

Розв’язуємо систему канонічних рівнянь відомими методами, наприклад, способом Гауса.

;

;

.

; ;

І.

.

ІІ.

.

ІІІ. ; .

Таблиця 2.1 – Розв’язання системи канонічних рівнянь по методу Гауса

№ рівняння
І (1)
ІІ	*
	*
ІІІ	*	*

Перевіряємо правильність розв’язання системи канонічних рівнянь.

;

;

.

Розв’язавши систему канонічних рівнянь, отримали значення основних невідомих переміщень:

Таким чином, розкрита кінематична невизначуваність рами.

2.8 Визначення дійсних внутрішніх зусиль та побудова епюр внутрішніх зусиль m, q, n

Отримавши значення й напрямок основних невідомих переміщень ; ; , будуємо епюру дійсних згинальних моментів за способом накладання, тобто як суму згинальних моментів в основній системі методу переміщень від дії кожного із визначених переміщень окремо (рис 2.15) та епюри згинальних моментів від зовнішнього навантаження в основній системі методу переміщень (рис. 2.9):

.

Парціальні епюри наведені на рис. 2.15. Для їхнього отримання одиничні епюри згинальних моментів, які побудовані в основній системі методу переміщень (рис 2.6, 2.7, 2.8) домножуються на величину відповідних переміщень з урахуванням їх знаків.

Остаточна епюра згинальних моментів () для заданої системи (рис 2.16) побудована як сума парціальної й вантажної епюр.

Будуємо епюру поперечних сил Q

За допомогою епюри згинальних моментів визначаємо поперечні сили в перерізах стержнів, розглядаючи кожний стержень рами як самостійну статично визначену балку навантажену зовнішнім вантажем (рис. 2.15) та опорними моментами, які беремо з епюри , враховуючи їх знаки.

Поперечну силу в перерізі стержня визначаємо за формулою:

.

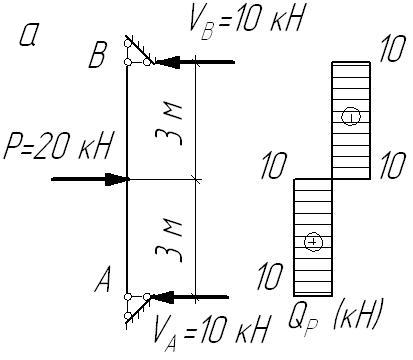
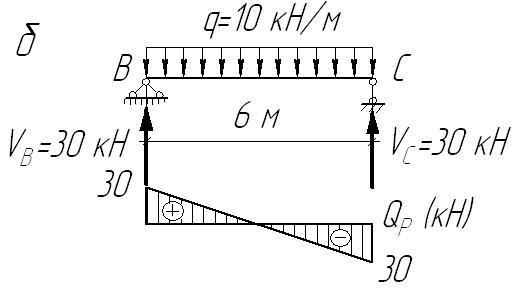
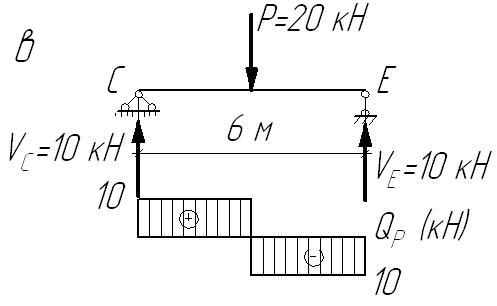
а) епюра для АВ; б) епюра для ВС; в) епюра для СЕ

Рисунок 2.15 – Епюри

кН;

кН;

кН;

м;

м.

;

кН∙м;

кН;

кН;

кН.

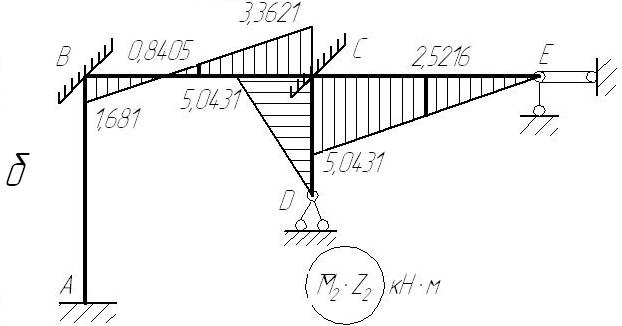
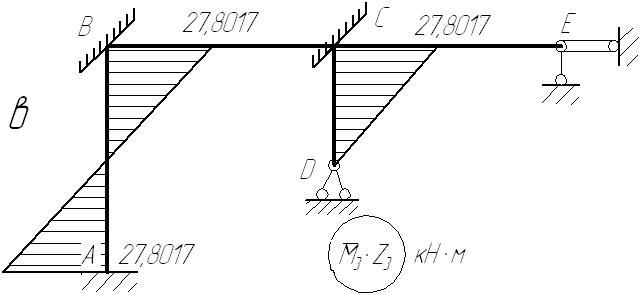
а) епюра ; б) епюра ; в) епюра

Рисунок 2.16 – Парціальні епюри згинальних моментів

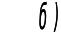
Рисунок 2.17 – Епюри дійсних внутрішніх зусиль

Епюра Qпобудована на рис.2.15 (б).

Будуємо епюру поздовжніх сил N. За допомогою епюри Q визначаємо поздовжні сили в стержнях із умов рівноваги вузлів рами, які послідовно (починаючи з вузла, де сходяться два стержні) виокремлюємо з епюри Q. Кожний вузол розглядається в рівновазі при дії на вузол (рис. 2.18) зовнішніх сил та внутрішніх зусиль. Задавшись додатнім від перерізу напрямком невідомої поздовжньої сили в стержні із умови рівноваги вузла визначаємо поздовжню силу в стержні.

Рисунок 2.18 – Рівновага вузлів рами при дії зовнішніх сил та внутрішніх зусиль

;

;

;

Епюра N побудована на рис. 2.15 (в).