2.6 Статичний спосіб визначення коефіцієнтів і вільних членів системи канонічних рівнянь та їх перевірка

Нагадаємо, що коефіцієнт, або вільний член системи канонічних рівнянь являє собою реактивну силу, що виникає у відповідній додатковій в’язі основної системи від одиничного значення невідомого переміщення , або від зовнішнього навантаження. Додатні напрями реактивних сил збігаються з напрямами відповідних невідомих переміщень. Зазначені реактивні сили поділяються на два види:

1. Реактивні моменти в рухомих «плаваючих» затисненнях.

2. Реакції в додаткових опорних стержнях.

Для визначення реактивних моментів у «плаваючих» затисненнях виокремлюємо вузол основної системи разом із затисненням з епюри згинальних моментів відповідного одиничного або вантажного стану. До вузла прикладаємо невідомий реактивний момент із додатнім напрямом у рухомому затисненні, а також згинальні моменти в перерізах стержнів. Складаємо рівняння рівноваги цього виокремленого вузла і визначаємо шуканий коефіцієнт.

Для заданої рами перший рядок коефіцієнтів системи канонічних рівнянь обчислюємо як реактивний момент у «плаваючому» затисненні 1 вузла В основної системи від одиничних невідомих переміщень і зовнішнім навантаженням (рис. 2.10).

Коефіцієнт – це реактивний момент у рухомому затисненні 1, від одиничного кута повороту , тобто в першому одиничному стані. Виокремлюємо вузол В з епюри і складаємо рівняння його рівноваги:

.

Коефіцієнт – це реактивний момент у рухомому затисненні 1, від одиничного кута повороту , тобто в другому одиничному стані. Виокремлюємо вузол В (рис. 2.11) з епюри і складаємо рівняння його рівноваги:

.

Коефіцієнт – це реактивний момент у рухомому затисненні 1, від одиничного поступального переміщення , тобто в третьому одиничному стані. Виокремлюємо вузол В (рис. 2.12) з епюри і складаємо рівняння його рівноваги:

.

Вільний член – це реактивний момент у рухомому затисненні 1, від зовнішнього навантаження, тобто у вантажному стані.

Виокремлюємо вузол В з вантажної епюри і складаємо рівняння рівноваги:

.

Другий рядок коефіцієнтів системи канонічних рівнянь обчислюємо як реактивний момент у рухомому затисненні 2 вузла С основної системи від одиничних невідомих переміщень і зовнішнього навантаження (рис. 2.11).

Коефіцієнт – це реактивний момент у рухомому затисненні 2, від одиничного кута повороту , тобто в першому одиничному стані. Виокремлюємо вузол С з епюри і складаємо рівняння його рівноваги:

.

Рисунок 2.6 – Одинична епюра переміщень від одиничного навантаження

Рисунок 2.7 – Одинична епюра переміщень від одиничного навантаження

Рисунок 2.8 – Одинична епюра переміщень від одиничного навантаження

Рисунок 2.9 – Одинична епюра переміщень від постійного навантаження

Коефіцієнт – це реактивний момент у рухомому затисненні 2, від одиничного кута повороту , тобто в другому одиничному стані. Виокремлюємо вузол С з епюри і складаємо рівняння його рівноваги:

.

Коефіцієнт – це реактивний момент у рухомому затисненні 2, від одиничного поступального переміщення , тобто в третьому одиничному стані. Виокремлюємо вузол С з епюри і складаємо рівняння його рівноваги:

.

Вільний член – це реактивний момент у другому затисненні 2, від зовнішнього навантаження, тобто у вантажному стані. Виокремлюємо вузол С з вантажної епюри і складаємо рівняння рівноваги:

.

Третій рядок коефіцієнтів системи канонічних рівнянь являють собою силові реакції в додатковому опорному стержні, введеному при створенні основної системи. Для обчислення їхньої величини необхідно розглянути умови рівноваги відокремленого перетином фрагмента основної системи (рис. 2.12).

Перетин повинен проходити через додатковий стержень, в якому обчислюється реакція, а також через усі стержні основної системи які зазнають перекосів у напрямі цього додаткового стержня від примусового поступального переміщення .

До відокремленого фрагмента слід прикласти всі сили, що діють на нього, в тому числі, зусилля в перерізах стержнів. Поперечні сили в перерізах отримують з епюр згинальних моментів на цих стержнях, за формулою:

.

Шукана реакція в додатковому опорному стержні визначається з рівняння рівноваги у вигляді суми проекцій на вісь у напрямку додаткового стержня (рис. 2.13).

Обчислюємо третій рядок коефіцієнтів системи канонічних рівнянь.

Коефіцієнт – це реакція накладеного опорного стержня 3 від одиничного кута повороту , тобто в першому одиничному стані. Для його визначення перетином, виокремлюємо фрагмент основної системи з рис. 2.6.

До цього фрагмента прикладаємо шукану реакцію перерізаного опорного стержня у напрямку, що збігається з напрямом невідомого переміщення та поперечні сили в перерізаних стержнях, які зазнають перекосів (рис. 2.13, а):

.

Реакцію визначаємо з рівнянь рівноваги фрагмента:

.

Коефіцієнт – це реакція накладеного опорного стержня 3 від одиничного кута повороту , тобто в другому одиничному стані. Виокремлюємо фрагмент основної системи з рис. 2.7. До цього фрагмента прикладаємо шукану реакцію та поперечну силу в стержні СD:

.

Реакцію визначаємо з рівнянь рівноваги фрагмента:

.

Коефіцієнт – це реакція накладеного опорного стержня від одиничного поступального переміщення , тобто в третьому одиничному стані. Для його визначення виокремлюємо той самий фрагмент у третьому одиничному стані основної системи (рис. 2.8). До цього фрагмента прикладаємо шукану реакцію та поперечні сили в перерізаних стержнях (рис. 2.13, в):

.

Реакцію визначаємо з рівнянь рівноваги фрагмента:

.

Вільний член – це реакція накладеного опорного стержня основної системи від зовнішнього навантаження, тобто у вантажному стані. Для цього виокремлюємо фрагмент основної системи (рис 2.9) у вантажному стані.

До цього фрагмента прикладаємо шукану реакцію та поперечні сили в перерізаних стержнях:

; .

Підставляємо визначені коефіцієнти в систему канонічних рівнянь і виконуємо перевірку їх значення.

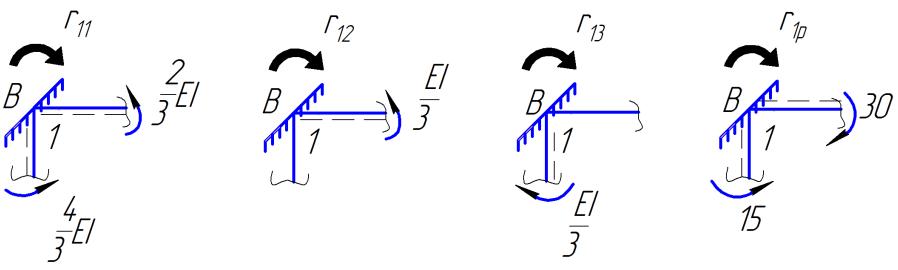
Рисунок 2.10 – Визначення коефіцієнтів канонічних рівнянь

Рисунок 2.11 – Визначення коефіцієнтів канонічних рівнянь

Перевірка правильності обчислення коефіцієнтів і вільних членів канонічних рівнянь.

Для перевірки правильності обчислення коефіцієнтів будуємо сумарну одиничну епюру згинальних моментів від одночасної дії всіх основних невідомих, які дорівнюють одиниці. Епюру (рис. 2.13) будуємо, як алгебраїчну суму ординат одиничних епюр згинальних моментів і виконуємо наступну перевірку:

.

Порядкова перевірка одиничних коефіцієнтів кожного рядку канонічних рівнянь полягає в тому, що сума одиничних коефіцієнтів « » рядку дорівнює результату перемноження сумарної одиничної епюри на одиничну епюру :

.

Універсальна перевірка одиничних коефіцієнтів у всіх рядках канонічних рівнянь полягає в тому, що сума всіх одиничних коефіцієнтів у всіх рядках дорівнює результату перемноження сумарної одиничної епюри на ту ж сумарну одиничну епюру.

.

Постовпцева перевірка вантажних коефіцієнтів у всіх рядках канонічних рівнянь полягає в тому, що сума вантажних коефіцієнтів дорівнює по значенню, але з протилежним знаком результату переміщення сумарної одиничної епюри на вантажну епюру, побудовану в статично визначеній системі методу сил , яку отримують із заданої розрахункової схеми відкиданням зайвих в’язей, у тому числі обов’язково й тих в’язей, реакції в яких відшукуються:

.

а) перевірка 1; б) перевірка 2; в) перевірка 3; г) перевірка 4

Рисунок 2.12 – Перевірка коефіцієнтів і вільних членів канонічних рівнянь

Перевіримо коефіцієнти канонічних рівнянь для заданої рами, підставивши та розділивши їх значення на EI.

	.

Порядкова перевірка

Рисунок 2.13 – Сумарна одинична епюра моментів

Рисунок 2.14 – Вантажна епюра моментів для статично визначеної системи

Універсальна перевірка

Постовпцева перевірка