Вопрос №1. Определение геодезии. Задачи инженерной геодезии при строительстве инженерных сооружений. Методы решения задач.

Геодезия – это наука о форме, размерах, гравитационном поле Земли, об измерениях на земной поверхности и способах ее изображения на картах, планах, профилях, цифровых моделях, а так же о решении других инженерных и народно-хозяйственных задач.

В процессе своего развития геодезия разделилась на ряд научных и

научно-технических дисциплин:

1) Высшая геодезия – изучает форму, размеры Земли вцелом, гравитационное поле, смещение земной коры, смещение магнитных полюсов.

2) Картография – изучает способы создания и использования картографической продукции

Картография делится на:

А) Топографию – изучает способы съемки местности с целью создания карт и планов

Б) Фотограмметрию – решает геодезические задачи посредством фототопографических и аэрофото снимков.

3) Космическая геодезия – решает различные геодезические задачи посредством искусственных спутников Земли.

4) Маркшейдерия – занимается решением геодезических задач в подземных выработках

5) Инженерная геодезия - рассматривает геодезические работы, выполняемые при изысканиях

проектировании в строительстве и эксплуатации инженерных сооружений.

Задачи инженерной геодезии:

1) Сбор геодезической информации, необходимой для разработки проекта на строительство сооружения.

2) Определение на местности основных осей будущего сооружения.

3) Определение формы, размеров, положения в пространстве конструктивных элементов сооружения в процессе его строительства и после его создания.

4) Определение деформаций сооружения.

Методы решения задач:

Прямая геодезическая задача: Определение координат конечной точки линии по координатам начальной точки, длине линии, и ее направлению.

Обратная геодезическая задача: Определение длины линии и ее направления по координатам начальной и конечной точек.

Методы решения научных и практических задач геодезии основываются на законах математики и физики. При помощи математики разрабатываются научно обоснованные схемы постановки и выполнения геодезических измерений и устанавливаются зависимости между результатами измерений и искомыми величинами. Задача изучения фигуры Земли и ее гравитационного поля решается на основе законов механики. Сведения из физики, в частности оптики, электроники и радиотехники необходимы для разработки геодезических приборов и правильной их эксплуатации. Геодезия так же связна с астрономией, геологией, геофизикой и др.

Вопрос №2. Сведения о формах и размерах Земли. Понятия: уровенная поверхность, геоид, земной эллипсоид, отвесная линия, уклонение отвесной линии, высота геоида.

Фигура Земли как планеты обусловлена воздействием многих процессов, связанных с ее образованием и существованием, решающее значение при этом оказывают силы, взаимного тяготения и центробежная сила.

Для изучения физической поверхности Земли вводится понятие уровенной поверхности.

Уровенная поверхность - поверхность, в каждой точке которой потенциал силы тяжести равны.

Уровенных поверхностей можно провести бесчисленное множество, и все они будут опоясывать Землю, нигде не пересекаясь друг с другом.

Потенциал силы тяжести – величина, численно равная работе по переносу единицы массы в поле силы тяжести Земли из бесконечности в данную точку.

За фигуру Земли принимают геоид.

Геоид – это тело, ограниченное уровенной поверхностью, совпадающей с уровнем воды в Мировом океане в состоянии полного покоя и равновесия и продолженного под материками.

Из всех геометрических фигур, определяемых простыми уравнениями, к геоиду ближе всего подходит сжатый эллипсоид т.е. тело, полученное вращением эллипса вокруг малой оси.

Земной эллипсоид - эллипсоид, который характеризует фигуру и размеры Земли.

Чтобы максимально приблизить поверхность земного эллипсоида к поверхности геоида, эллипсоид соответствующим образом ориентируют в теле Земли. Такой эллипсоид называют референц-эллипсоидом.

Эллипсоид вращения – математическая модель геоида. ( Эллипсоид Красовского)

А = 6 378 245 м – большая ось эллипсоида.

В = 6 356 863 м – малая ось эллипсоида.

Отвесная линия – прямая, совпадающая с направлением действия силы тяжести в данной точке.

Уклонение отвесной линии – угол между отвесной линией и нормалью к поверхности земного эллипсоида в данной точке.

Высота геоида – высота поверхности геоида над поверхностью земного эллипсоида по нормали к нему в данной точке.

Вопрос №3. Системы координат, применяемые в геодезии (геодезические, астрономические, плоские прямоугольные геодезические, топоцентрические). Система счета высот.

В инженерной геодезии применяют несколько типов координат:

Геодезические координаты - три величины, две из которых характеризуют направление нормали к поверхности земного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третья является высотой точки над поверхностью земного эллипсоида.

Геодезическая широта – угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью экватора.

Геодезическая долгота – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического меридиана.

Достоинство геодезических координат заключается в возможности обработки результатов геодезических измерений в единой для всей поверхности Земли системе координат.

Астрономические координаты - компоненты направления отвесной линии в данной точке пространства относительно плоскости, перпендикулярной к оси вращения Земли, и плоскости начального астрономического меридиана.

Астрономическая широта – угол, образованный отвесной линией в данной точке и плоскостью перпендикулярной к оси вращения земли.

Астрономическая долгота – двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана.

В инженерно –геодезических работах, как правило, нет необходимости различать геодезические и астрономические координаты.

Плоские прямоугольные геодезические координаты - прямоугольные координаты на плоскости, на которой отображена по определенному математическому закону поверхность земного эллипсоида.

Решение геодезических задач в данной системе выполняется по простым формулам аналитической геометрии. Для этого нужно сначала перенести все элементы поверхности на плоскость. Это будет происходить с искажением, но эти искажения малы и легко учитываются.

Топоцентрические координаты - координаты, началом счета которых является точка местности.

Геодезическая высота – высота точки над поверхностью земного эллипсоида.

Ортометрическая высота – высота точки над поверхностью геоида.

В инженерно –геодезических работах, как правило, нет необходимости различать эти системы высот.

Вопрос №4. Понятия: топографическая карта, план.

Карта - построенное в картографической проекции, уменьшенное, обобщенное изображение поверхности Земли, другого небесного тела или внеземного пространства, показывающее расположенные на них объекты в определенной системе условных знаков.

Топографическая карта – это подробная карта участка местности, позволяющая определить плановое и высотное положение точек.

Карта является наглядной и измеримой моделью местности, дающей ясное представление о ее характере и свойствах. Основные элементы местности (реки, озёра, населённые пункты) изображаются в действительных очертаниях и размерах в соответствии с масштабом карты. Внемасштабными знаками отмечают какие-либо заметные объекты на местности — башни, отдельно стоящие деревья, колодцы, родники и т.д. На топографических картах и планах неровности поверхности Земли — рельеф — показаны в виде горизонталей. Горизонталь – линия равных высот на карте. Они проводятся через равное число метров по высоте.

Топографический план - картографическое изображение на плоскости в ортогональной проекции в крупном масштабе ограниченного участка местности, в пределах которого кривизна уровенной поверхности не учитывается.

Отличие плана от карты: на плане изображаются небольшие участки земной поверхности, на картах же изображены гораздо большие территории и в более мелком масштабе. На план наносятся все объекты и детали местности в заданном масштабе. На карты объекты отбирают в зависимости от их содержания и назначения.

Горизонтальное проложение – длина проекции отрезка на плоскость.

Решением задач на картах и планах является определение:

1) географических координат точек (линейка),

2) дирекционного угла, истинного и магнитного азимутов линий (транспортир),

3) отметок точек

4) крутизны ската, построение профиля, линий с заданным уклоном и тд.

Вопрос №5. Понятия: масштаб, точность масштаба. Виды масштабов: численный, именованный, графические.

Масштаб – это отношение длины отрезка на карте к длине горизонтального проложения этого отрезка на местности.

Масштабы бывают нескольких видов:

1)Численный масштаб обычно представляют в виде правильной дроби, числитель которой равен единице, а знаменатель некоторому числу. (1:50)

2)Для удобства чтения численный масштаб записывают в виде именованного масштаба, например «в 1 сантиметре 50 метров»

3)Так же существуют графические масштабы:

А) Линейный масштаб используют для измерения с небольшой точностью длин отрезков на плане. Он представляет собой прямую линию, разделенную на равные отрезки, длина одного отрезка называется основанием масштаба. Она соответствует определенному числу метров на горизонтальном проложении. Левое крайнее основание линейного масштаба разделено на более мелкие деления.

Горизонтальное проложение – длина проекции отрезка на плоскость.

Б) Поперечный масштаб применяют для более точных измерений длин отрезков на планах. Его гравируют на специальных металлических линейках. Он позволяет измерять расстояния с точностью цены наименьшего деления.

Точность масштаба – длина горизонтального проложения линии местности, соответствующая на плане отрезку в 0,1 мм.

Вопрос №6. Разграфка и номенклатура топографических карт.

Разграфка – это разбиение многолистной карты на отдельные листы по определенной системе.

Номенклатура – обозначение листа многолистной карты по определенной системе.

Топографические карты делятся на отдельные листы линиями меридианов и параллелей. Это удобно тем, что рамки листов точно указывают положение на земном эллипсоиде участка местности, изображённого на данном листе, и его ориентировку относительно сторон горизонта.

В основе разграфки и номенклатуры топографической карты лежит карта масштаба 1:1 000 000.

Листы этой карты по параллелям образуют четырехградусные ряды, а по меридианам шестиградусные колонны.

Ряды листов этой карты обозначаются заглавными буквами латинского алфавита (от А до V) и счёт их ведётся от экватора к полюсам. Колонны же листов нумеруются цифрами от 1 до 60. Счёт колонн ведётся от меридиана 180 градусов с запада на восток.

Для подбора нужных листов карт на тот или иной район и для быстрого определения их номенклатуры существуют так называемые сборные таблицы карт . Они представляют собой мелкомасштабные схемы, разделённые меридианами и параллелями на клетки, соответствующие обычным листам карты масштаба 1:100 000, с указанием их порядковой нумерации в пределах листов миллионной карты.

Лист карты масштаба 1:100 000 получается делением листа миллионной карты на 144 части, номенклатура его состоит из обозначения листа карты 1:1000 000 с добавлением одного из чисел 1, 2, 3, 4, ..., 143, 144.

Рассмотрим номенклатуру карты:

У-33-65-Б

У – номер ряда по карте 1:1 000 000

33 – номер колонны по карте масштаба 1: 1 000 000

65 – номер ячейки по карте масштаба 1:100 000

Б – номер листа карты масштаба 1:50 000

Вопрос №7. Понятие о системе плоских зональных прямоугольных координат. Координатная сетка на топографических картах.

Плоские системы координат применяются для проведения съемочных работ и отображения участков земной поверхности на плоскости в виде карт и планов.

Для отображения на плоскости значительных территорий земной поверхности применяются картографические проекции, дающие возможность переносить точки с поверхности эллипсоида на плоскость по определенным математическим законам.

В нашей стране используется равноугольная проекция Гаусса-Крюгера. Вся поверхность Земли делится на 6-градусные (по долготе) зоны ( от полюса до полюса), которые каждая отдельно разворачиваются в плоскую поверхность. Всего образуется 60 таких зон, которые нумеруются цифрами от 1 до 60 против хода часовой стрелки, начиная от Гринвича. Зона — это участок земной поверхности, ограниченный двумя меридианами.

Осевой меридиан принимают за ось абсцисс, а линию экватора - за ось ординат. За начало координат принимают точку 0 пересечения осевого меридиана с экватором. Чтобы не иметь отрицательных ординат, ординату осевого меридиана считают равной не нулю, а 500 км.

Для удобства использования плоских координат на листе карты показывают километровую сетку — семейство линий параллельных экватору и осевому меридиану.

Система разбиения на шестиградусные зоны тесно связана с построением системы разграфки и номенклатуры листов топографических карт разных масштабов. Каждой шестиградусной зоне соответствует одна колонна листов карты 1:1000 000. В основе разграфки и номенклатуры лежит лист карты масштаба 1:1000000, который имеет размеры 4° по широте и 6° по долготе.

В каждой координатной зоне строится координатная сетка. Она представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проведены через целое число километров.

На топографических картах значения абсцисс и ординат координатных линий подписывают у выходов линий за внутренней рамкой листа и девяти местах на каждом листе карты. Полные значения абсцисс и ординат в километрах подписываются около ближайших к углам рамки карты координатных линий и около ближайшего к северо-западному углу пересечения координатных линий. Остальные координатные линии подписываются сокращенно двумя цифрами (десятки и единицы километров). Подписи около горизонтальных линий координатной сетки соответствуют расстояниям от оси ординат в километрах.

Подписи около вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от осевого меридиана зоны на 500 км.

Координатная сетка на карте используется при определении прямоугольных координат и нанесении на карту точек (объектов, целей) по их координатам, измерении по карте дирекционных углов направлений, целеуказании, отыскании на карте различных объектов, приближенном определении расстояний и площадей, а также при ориентировании карты на местности.

Вопрос №8. Понятие – ориентирование линии. Истинный и магнитный азимуты линии. Дирекционный угол линии. Румб. Зависимость между ориентирующими углами. Сближение меридианов. Склонение магнитной стрелки.

Ориентировать линию – значит определить ее направление относительно исходного.

В качестве углов, определяющих направление линий, служат азимуты, румбы и дирекционные углы.

Истинный азимут (географический) – это двугранный угол между плоскостью географического меридиана данной точки и вертикальной плоскостью, проходящей по данному направлению.

Магнитный азимут – горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана до направления на предмет.

Дирекционный угол – это угол между проходящим через данную точку направлением и линией, параллельной оси абсцисс, отсчитываемый от северной части оси абсцисс по ходу часовой стрелки.

Румб – это острый угол, отсчитываемый от северной или южной части линии параллельной оси абсцисс до заданного направления.

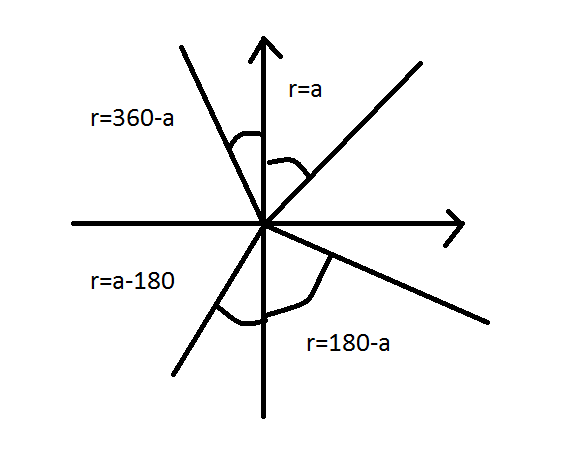
Сближение меридианов – угол между направлением осевого меридиана и географическим меридианом данной точки.

Склонение магнитной стрелки – угол между истинным меридианом и магнитным меридианом.

А_и=а+(+/- δ)

А_и=А_м+(+/-γ) γ-склонение магнитной стрелки

Вопрос №9. Сущность метода горизонталей. Основные формы рельефа местности и их изображения на топографических картах и планах методом горизонталей.

Рельеф – это совокупность неровностей земной поверхности (в том числе дна моря или океана).

Способы изображения рельефа на картах:

1. Способ отмывки

2. Способ горизонталей

3. Способ отметок

Основные формы рельефа:

Местность по рельефу разделяется на равнинную, холмистую(пересеченную) и горную.

Из многообразия форм рельефа можно выделить наиболее характерные:

1) Гора, холм, сопка.

2) Котловина(впадина).

3) Хребет (вытянутая возвышенность).

4) Лощина (вытянутое углубление). И т.д.

Способ горизонталей:

Учету рельефа при проектировании строительства всех видов сооружений придается первостепенное значение. На современных топографических картах и планах рельеф изображается горизонталями.

Горизонталь – линия равных высот на карте.

Мы мысленно сечем поверхность горизонтальными плоскостями, параллельными друг другу.

Расстояние между соседними горизонталями называется заложением.

Высота сечения рельефа – это расстояние по отвесной линии между соседними секущими уровенными поверхностями. Она задается в зависимости от масштаба карты и характера рельефа.

Для определения направлений скатов на некоторых горизонталях проводят короткие черточки в направлении ската – бергштрихи.

Вопрос №10. Крутизна и направление ската; графики заложений.

Крутизна ската – угол, образованный направлением ската с горизонтальной плоскостью в данной точке.

Направление ската обозначается на картах и планах бергштрихами.

Крутизна ската по направлению определяется двумя показателями : уклоном(i) и углом наклона(ν).

tgν=h/a=i;

Для графического определения углов наклона по заданному значению a, масштабу М и высоте сечения рельефа h строят график заложения.

Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. По перпендикуляру к основанию графика от этих точек откладывают отрезки, равные соответствующим заложениям. Концы отрезков соединяют плавной кривой.

Аналогично строят график заложения для уклонов.

Определение высоты точки:

X=(l₁*h)/L

H_a=H₁+x

L-заложение ската

Вопрос №11. Составляющие погрешности, основные причины их появления. Выявление грубой и систематической составляющей погрешности, их устранение.

Все результаты измерения физической величины имеют погрешность. Если результат измерения равен точному значению физической величины, то это получилось случайным образом.

Погрешность разделяют на три составляющие:

1) Грубая погрешность(невнимательность, неисправность прибора)

Для выяснения наличия грубой погрешности каждую физическую величину необходимо измерить минимум два раза.

∆l=l₁-l₂ ;

∆l ≤ ∆l_пред.

∆l_пред. Указана в инструкциях на каждый вид измерения.

Если грубая погрешность есть, необходимо зачеркнуть предыдущие результаты измерения и выполнить новые.

Выполняют измерения до тех пор, пока не будет выполняться данное условие.

Данная поверка выполняется на местности, сразу после измерения физической величины.

2) Систематическая погрешность – погрешность средств измерения, методов и способов измерения. (закономерная погрешность)

Вводят поправку, тем самым исключая данную погрешность.

Можем рассчитать и результаты измерения от систематической погрешности освобождаются.

3) Случайная погрешность (невнимательность)

∆=l-x

Х - Точное значение физической величины.

L – результат измерения этой величины.

Рассчитывается случайная погрешность, так как l в себе не имеет грубой погрешности и систематической погрешности.

Причины появления погрешности:

1) Изменение величины объекта со временем

2) Личные погрешности наблюдателя

3) Показатели прибора

4) Метод измерения

5) Непрерывное изменение внешних условий

Вопрос №12. Критерии оценки точности результатов измерений.

Измерения бывают двух видов: равноточные и неравноточные.

Равноточные измерения – это измерения выполненные в одинаковых условиях.

Условия:

1) одни и те же погодные условия

2) одна и та же точность средств измерения

3) одна и та же квалификация исполнителей

4) одни и те же методы и способы измерения

Под точностью измерений понимают качество измерений, определяющее близость их результатов к точному значению физической величины.

Точное значение физической величины, если оно не определяется теоретически – неизвестно.

В качестве основной меры точности принят стандарт. Однако его точное значение определить нельзя, поэтому на практике пользуются его приближенным значением – средней квадратической погрешностью:

m=√∑∆²/n,

по полученному значению можно найти случайную погрешность.

∆_пред=2m.

Вопрос №13. Обработка ряда равноточных измерений ( средняя квадратическая погрешность результата измерения физической величины, арифметическая средина и ее средняя квадратическая погрешность).

Равноточные измерения – это измерения выполненные в одинаковых условиях.

Математическая обработка ряда равноточных линейных измерений при неизвестном значении измеряемой величины.

Х=∑l_i/ n, где l_i– результаты измерений, n – количество измерений, Х–арифметическая средина;

m=√∑V²/(n-1) (Формула Бесселя), где m – средняя квадратичная погрешность

m_e=m/√n, где m_e – средняя квадратичная погрешность

V = l – X, где V – отклонение от арифметической средины;

Математическая обработка ряда равноточных линейных измерений при известном значении измеряемой величины.

∆=l_i–Х, где ∆–погрешностьизмерений, l_i– результаты измерений;

m=√∑∆²/n, где m –средняя квадратичная погрешность.

∆_ср =∑׀∆׀/n, где n – количество измерений, ∆_ср – средняя погрешность измерений;

ВЫВОДЫ СМОТРЕТЬ В ТЕТРАДИ!

Вопрос №14. Обработка ряда неравноточных измерений (понятие о весе, общая арифметическая средина и ее квадратическая погрешность, средняя квадратическая погрешность единицы веса).

Неравноточными называют измерения, выполненные в различных условиях, приборами различной точности, различным числом приемов и т.д.

Надежность результата, выраженная числом называется его весом.

р=с/m², где р– вес, с – число(частный случай c = m₁² ).

Х₀=∑рl/∑р, где Х₀–общая арифметическая средина, l – результат измерений;

m_e=µ/√∑р где m_e–средняя квадратичная погрешность общей арифметической средины.

µ=√∑р∆²/n, гдеµ –средняя квадратичная погрешность единицы веса;

Вопрос №15. Понятия: горизонтальный и вертикальный углы. Приборы для измерения углов.

Угловые измерения производят для того, чтобы определить в пространстве взаимное положение точек местности.

Горизонтальный угол – это двугранный угол, ребром которого является отвесная линия, проходящая через точку.

Вертикальный угол – угол, лежащий в вертикальной плоскости.

В геодезии измеряются вертикальные углы, образованные горизонтальной линией и наклонной линией(наклонную линию образует визирная ось)

Приборы для измерения углов:

1) Теодолит

2) Тахеометр

3) Кипрегель

4) Эклиметр

Теодолит – это геодезический прибор для измерения горизонтальных и вертикальных углов.

Вопрос №16. Классификация теодолитов по ГОСТ.

Теодолит – это геодезический прибор для измерения горизонтальных и вертикальных углов.