Билет 6. Закон сохранения импульса в изолированной системе из двух материальных точек.

Излированной или замкнутой системы. Так называют систему тел, настолько удаленных от всех остальных тел, что они практически не оказывают никакого действия на рассматриваемую систему. Тела системы могут взаимодействовать только между собой. Рассмотрим теперь изолированную систему, состоящую из двух материальных точек. Скорости точек должны быть малы по сравнению со скоростью света. В результате взаимодействия материальных точек их скорости меняются. Пусть v1 — скорость точки 1, v2 — скорость точки 2, a Δv1 и Δv2 — приращения этих скоростей за один и тот же промежуток времени Δt. Величины Δv1 и Δv2 имеют противоположные направления и связаны между собой соотношением m1Δv1=−m2Δv2 , где величины m1 и m2 постоянны и имеют одинаковые знаки. Они совершенно не зависят от характера взаимодействия между материальными точками 1 и 2. Например, взаимодействие может происходить путем столкновения материальных точек между собой. Его можно осуществить, сообщив материальным точкам электрические заряды или поместив между ними маленькую пружинку и т.д. Продолжительность времени Δt можно менять произвольным образом. Векторы Δv1 и Δv2 при этом будут меняться. Однако коэффициенты m1 и m2, точнее, их отношение, останутся одними и теми же. Эти результаты надо рассматривать как опытные факты, подтвержденные бесчисленным множеством примеров. Коэффициенты m1 и m2 могут зависеть только от самих материальных точек системы. Они называются массами или, точнее, инертными массами материальных точек 1 и 2.

Таким образом, по определению, отношение масс двух материальных точек равно взятому с противоположным знаком отношению приращений скоростей этих точек в результате взаимодействия между ними. При этом предполагается, что рассматриваемые точки образуют изолированную систему и движутся с нерелятивистскими скоростями.

Билет 7. Теорема о движении центра масс.

Важное значение для системы материальных точек имеет такое понятие, как центр масс. Сначала рассмотрим две материальные точки с массами m₁ и m₂ и найдём их центр масс. В данном случае центр масс - это точка С, которая лежит на прямой соединяющей материальные точки. Если положение материальных точек описывается радиус-векторами и , то положение центра масс С, будет описываться радиус-вектором , который равен . В общем случае системы из n материальных точек, положение центра масс будет описываться радиус-вектором: = , где M = m₁ + m₂ + ... + m_n - полная масса системы материальных точек. Взяв производную, получим скорость центра масс: . Если система материальных точек замкнута, то , и тогда .

Таким образом, при отсутствии внешних сил центр масс системы материальных точек остается в покое или движется прямолинейно и равномерно

Центр масс системы движется так как двигалась бы м/т с массой равной масс всей системы под действием результирующей всех внешних сил действующих на систему.

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. F^e –общ обозначение внешней силы (экстерьер – снаружи), Fⁱ– общее обозначение внутренних сил (интерьер – внутри) Ma_C= ∑F^e_i Центр масс системы движется, как материальная т, масса которой равна массе всей системы, и к которой приложены все внешние силы, действующие на систему. (2 формулировки).

БИЛЕТ 8. Движение тел с переменной массой. Уравнение Мещерского, уравнение Циолковского.

Уравнение движения тела с переменной массой

На выполнении закона сохранения импульса основано движение ракеты, если её рассматривать как замкнутую систему. Мы рассмотрим более общий случай движения тела с переменной массой при наличии внешней силы, например, движение ракеты в гравитационном поле Земли.

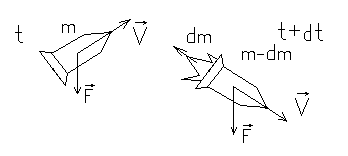Для этого рассмотрим два близких момента времени t и t+ dt и вычислим изменение импульса системы: ракета + вытекающий газ. Пусть в момент времени t импульс системы равен .За время dt выброшен газ массой dm со скоростью относительно ракеты, и импульса системы: ракета + газ стал равен: . В выражении для раскроем скобки и пренебрежем малой величиной более высокого порядка ( ) . Тогда изменение импульса системы: ракета + газ за время dt равно: , . Подставляя это во второй закон Ньютона , получим уравнение движения тела с переменной массой: - уравнение Мещерского. Второй член справа в этом уравнении представляет собой - силу реактивной тяги, где — секундный расход топлива.