БИЛЕТ 1. Скорость движения точки по прямой. Мгновенная скорость. Нахождение координаты по известной зависимости скорости от времени. Траектория, путь , перемещение. Скорость точки есть физическая величина, определяющая изменение координаты с течением времени.
Величина средней скорости численно равна отношению пройденного точкой расстояния по времени, за которое это расстояние было пройдено.
v
=
(x
-
x
)/(t
-
t
). В
момент времени t
тело было в точке х
и
в момент t
в
х
.
Равномерность скорости равна отношению двух величин, длины и времени.
Средняя скорость зависит от промежутка времени, за которое мы ее определяем.Если средняя скорость для любого промежутка времени для данного движения одинакова, то это движение происходит с постоянной скоростью и называется равномерным.
Ср. скорость не указывает нам изменение движения тела в различных местах пути, поэтому для более полной характеристики движения вводим мгновенное значение скорости в данный момент времени или скорость точки в данным момент времени.
Перемещение
точки
,
которое совершило перемещение за время
.
Расстояние,
пройденное точкой за время t
-
t
при
постоянной скорости равно произведению
скорости на время.
Положение
материальной точки в момент времени t
можно задать тремя координатами х, у, z
или радиус-вектором r,
соединяющим с ней начало координат. В
процессе движения материальная точка
описывает пространственную кривую
— траекторию.
Движение точки полностью определяется
заданием закона движения — трех функций
x(t), y(t), z(t) или, что то же самое, одной
векторной функции
.
Путь — это длина участка траектории, пройденного точкой за определенный интервал времени. Путь — величина скалярная, т.е. не зависящая от выбора системы координат. Путь не может быть отрицательным и не может убывать со временем.
Перемещением материальной
точки на интервале времени от момента
t1 до
момента t2 называется
вектор 
,
соединяющий начальное положение точки
с конечным. Очевидно, что 
т.е.
перемещение равно разности радиусов-векторов
точки в конечный и начальный моменты
времени. Если начальный момент времени
не указан, то перемещение отсчитывается
от начала движения: 
—
радиус-вектор в начальный момент времени
(при t = 0).
Билет 2. Векторный и координатный способы описания движения точки. Скорость и ускорение.
Векторный
способ
Положение
материальной точки задается с помощью
радиуса-вектора 
относительно
некоторой неподвижной точки О.
- вектор
перемещения материальной
точки за время 
.
-
вектор средней
скорости.
-
вектор мгновенной
скорости.
- среднее
ускорение,
- мгновенное
ускорение МТ.
Закон движения может быть представлен в виде r(t) = x(t)i +y(t)j+z(t)k.
Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.
Координатный способ.
Если с системой отсчета связать декартову систему координат (X, Y, Z) , то положение материальной точки А можно задать с помощью координат (x, y, z). Траекторию движения мы определим, если будем знать функцию x(t), y(t), z(t).
БИЛЕТ 3. Баллистическое движение.
Баллистика - раздел механики, изучающий движение тел в поле тяжести Земли.
Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по оси х и равнопеременного движения по оси у.
Tам же вы получили уравнение, описывающее траекторию движения тела в поле тяготения Земли - это парабола.
БИЛЕТ 4. Равномерное движение материальной точки по окружности. Криволинейное движение точки в пространстве.
Полное
ускорение в этом движении равно
нормальному ускорению (или
центростремительному): 
=
n и
направлено перпендикулярно к направлению
вектора скорости , по радиусу к центру
окружности. При этом движении радиус-вектор
т. М поворачивается на угол 
=
–
0 за
интервал времени
t
= t – t0,
а его конец описывает дугу окружности.
При
вращении угол поворота
изменяется
с течением времени, тогда уравнение
=
(t)
– это уравнение вращения. Угол
(или
)
аналогичен величине линейного пути S
при поступательном движении, и его
называют углом поворота или угловым
путем. Элементарное угловое перемещение
–
это вектор, направленный вдоль оси по
правилу правого винта и численно равный
углу
.
Средняя
угловая скорость 
cp –
это физическая величина, равная отношению
угла поворота к интервалу времени, за
который оно произошло.
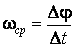
Мгновенная
угловая скорость
мгн –
это физическая величина, равная пределу
отношения углового перемещения
к
интервалу времени, за который оно
произошло (при
t 
0).
Угловая скорость – производная от угла поворота по времени.
При равномерном движении по окружности вокруг закрепленной оси, при котором за любые равные промежутки времени радиус-вектор точки поворачивается на одинаковые углы, угловая скорость может рассматриваться как скаляр:
cpмгн =
const 
;
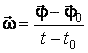
При
равномерном вращении модуль угловой
скорости: 
Уравнение равномерного движения материальной точки по окружности:
или
Среднее
угловое ускорение 
cp –
это физическая величина, равная отношению
изменения вектора угловой скорости к
интервалу времени, за который оно
произошло.
.
Мгновенное угловое ускорение – это
физическая величина, равная пределу
отношения изменения угловой скорости
к интервалу времени, за который оно
произошло (при
t
0).
; 
.
Угловое ускорение – производная от угловой скорости по времени или вторая производная от угла поворота по времени:
; 
.
При равномерном движении по окружности = 0. Равномерное движение точки по окружности – это периодическое движение.
Частота вращения v – это физическая величина, обратная периоду, и характеризует число полных оборотов за единицу времени.
,
,
где N – число полных оборотов за единицу
времени.
Линейная скорость (мгновенная скорость при движении по окружности):
.
При
t
= Т,
S = 2
R
, v
= 2
Rv
Угловая скорость (34) при t = Т равна:
.
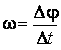Угловой путь при равномерном движении материальной точки по окружности:
.
Уравнение
равномерного движения материальной
точки по окружности:
При
t
= Т,
=
2p
, w
= 2
v.
Связь линейной и угловой скорости
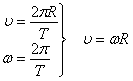
Связь тангенциального ускорения аt и углового ускорения
аt = R.