Вычислительный эксперимент. Дискретизация исходной математической задачи

Приближенным числом (ПЧ) а, полученным в результате измерения, счета или выполнения разнообразных математических операций называют приближенным (ПЧ), если оно незначительно отличается от точного А.

Абсолютная погрешность числа x =А – a

Предельная относительная погрешность a=a /a

Исчисление конечных разностей. Разностные уравнения

1. Оператор нисходящих (правых ) разностей y(x)= y(x+h) - y(x) или y_к=y_к+1 - y_к

2. Оператор восходящих (левых ) разностей y(x)= y(x) - y(x-h) или y_к=y_к - y_к-1

3. Оператор центральных (средних) разностей y(x)= y(x+h/2)- y(x - h/2)

Разностным уравнением порядка k табличной функции f называют уравнение вида:

y_{n =} F( y_n-1, y_n-2 , …y_n-к , х ) , где F известная функция (k+1) переменных. Это уравнение представляет собой рекуррентную формулу, позволяющую по известным значениям функции f в k последовательных точках найти её значение в следующей точке.

Прикладные задачи интерполяции и аппроксимации и их алгоритмизация. Методы и алгоритмы решения линейных алгебраических уравнений

Получение эмпирической формулы по табличным данным называют задачей аппроксимации, а вычисление значения функции, заданной таблично, в промежутках между узлами аргумента называют задачей интерполяции.

Интерполяция представляет собой точечную аппроксимацию функций. Задача ставится следующим образом: для данной табличной функции {X_i,Y_i} со значениями в n +1 точке, построить функцию y = f(x) в форме степенного многочлена степени Pn (x) не выше n, принимающего в заданных точках те же значения, что и функция {X_i,Y_i}, т.е. v(xi) = yi

1. Интерполяция с помощью линейного полинома.

Так, при значениях табличной функции n +1=2 Pn(x) = a₀ + a₁x. Для получения a₀, a₁ воспользуемся значением xi, yi. Для этого нужны две узловые точки (x₀, y₀), (x₁, y₁)_, . Тогда, по заданному критерию нужно решить систему из двух уравнений, что позволяет найти значения a0 и a1:

a₀ + x₀ a₁ = y₀

a₀ + x₁ a₁ = y₁

Пример 1. x₀ = 1 y₀ =5.2 , x₁ = 2, y₁ = 8.6

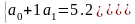
Решив эту систему методом Крамера, получим a₀ = 1.8; a₁= 3.4.

2. Интерполяционный полином, формулу для которого предложил математик Ж. Лагранж в 1793 году.

При наличии n+1 узлов

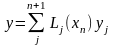, где

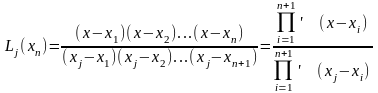, где знак ´

штрих у знака произведения означает “исключая j – е значение”

Так при n=1 полиномы L(x) запишутся так:

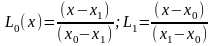
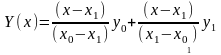
При n=2

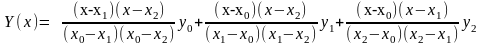При n=3 будет четыре слагаемых и т. д. При кратных узлах вычисления полинома упрощаются.

Если число узлов табличной функции велико (особенно при проведении эксперимента), то для приближения аналитической функции используют метод аппроксимации.

Методы решения СЛАУ

Прямые методы: Крамера и Гауса

Итерационные методы:

Метод Гаусса - Зейделя отличается от метода простой итерации лишь тем, что при вычислении (k+ 1) приближения, полученные x^(k+1) компоненты вектора x^(k+1) сразу же используются в вычислениях.

x₁^(k+1) = b₁₁ x₁^(k) + b₁₂ x₂^(k) +.....+ b_1n x_n^(k) + d₁

x₂^(k+1) = b₂₁ x₁^(k+1) + b₂₂ x₂^(k) +.....+ b_2n x_n^(k) + d₂

_{.......................................................................................................}

x_n^(k+1) = b_n1 x₁^(k+1) + b_n2 x₂^(k) +.....+ bn_1n x_n^(k) + d_n

Начальный вектор X⁽⁰⁾ задается k = 0, 1, 2 ... В матричной записи это можно представить так:

X^(k+1) = Ux^(k) +Lx^(k+1) + d , где матрицы U, L получены разложением В в сумму В = U + L

U - верхняя треугольная часть матрицы В, включая диагональ;

L - нижняя под диагональная матрицы B т.е. в методе Гаусса - Зейделя C = ( E - L ), B = U .

Условие сходимости итерационного процесса ||( E - L )^-1 B|| < 1

Задана СЛАУ. Решить методом простой итерации.

4x₁+ 0.24x₂ – 0.08x₃ = 8 x₁ = 2 – 0.06x₂ + 0.02x₃

0.09x₁ + 3x₂ – 0.15x₃ = 9 x₂ = 3 – 0.03x₁ + 0.05x₃

0.04x₁ – 0.08x₂ + 4x₃ = 20 x₃ = 5 – 0.01x₁ + 0.02x_{2 Нулевое приближение (свободные члены)}

_{Исходная система Преобразованная система || B || = {0.08, 0.08, 0.03} Условие сходимости соблюдается.}

_{Условие сходимости – диагональные коэффициенты должны быть больше суммы остальных в матрице исходной СЛАУ.}

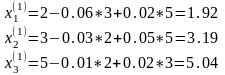Первое приближение

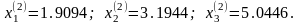Второе приближение

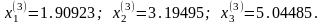Третье приближение

Итерации можно прекратить, так как разница между вторым и третьим приближением мала.

Формула линейной интерполяции y_i = (x-x₀)/(x₁-x₀)×( y₁ - y₀) + y₀

Методы численного дифференцирования

Если известна таблица функции и первые разности, то производная в точке х₁ следующим образом

Таблица 1

xi	yi	разности
x0	y0	y = y1- y0
x1	y1	y = y2 - y1
x2	y2	y = y2 – y0

dy / dx = ( y₂ – y₁ ) / h - с помощью левой восходящей разности

dy / dx = ( y₁ – y₀ ) / h - с помощью правой нисходящей разности

dy / dx = ( y₂ – y₀) / 2h - с помощью центральной разности, где h – шаг табличной функции.

Пример 1. Вычислить производную в точке х = 1 для функции y = x³, если известна таблица функции.

x	0.7	0.8	0.9	1.0	1.1
y	0.343	0.512	0.729	1.0	1.331
			y0	y1	y2

Выберем два значения табличной функции справа (y₂) и слева (y₀) от точки, в которой надо вычислить значение производной. Используя таблицу 1, вычислим значения производной.

f(x, h) = y' (1;0.1) = [y(1.1) - y(1.0)]/0.1 = (1.331 - 1.0)/0.1 = 3.31

f(x, h) = y'(1;0.1) = [y(1.0) - y(0.9)]/0.1 = (1-0.729)/0.1 = 2.71

f(x, 2h) = y'(1;0.2) = [y(1.1) - y(0.9)]/0.1 = (1.331 - 0.729)/0.2 = 3.01

Точное значение производной y' (1) = 3 1.0² = 3 (конечно-разностный метод имеет первый порядок точности). Как видно на примере, наименьшую погрешность дает формула центральной разности (абсолютная погрешность 0.01; относительная погрешность 0.33%).

Производную можно вычислять численно через значения функции, если использовать интерполяционный полином Лагранжа. Для трех узлов табличной функции с постоянным шагом производная от интерполяционного полинома Лагранжа имеет следующий вид:

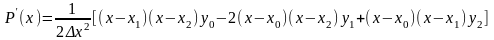
Для вычисления производной в точке x₀ в общую формулу подставим x = x₀ , и раскроем скобки.

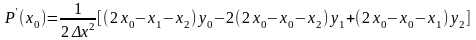
Если провести вычисления и привести подобные, то можно получить выражение для вычисления производной по трем значениям табличной функции

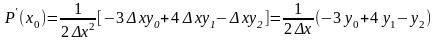
По аналогии для x = x₁

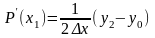
и для x = x₂. Видно, что это центральная разность.

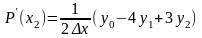
Пример 2.

Вычислить производную для той же табличной функции в точке х = 0.9 по формуле Лагранжа. Выделим три значения функции: y₀ = 0.729; y₁ =1.0; y₂ = 1.331.

y' (0.9;0.1) =1/0.2(-30.729+41.0 - 1.331)= 2.41. Точное значение производной 30.9²= 2.43, что значительно точнее, чем через первые разности.

Можно взять и другие точки: y₀ =0.343; y₁ =0.512; y₂ = 0.729.

Тогда производную надо вычислять по другой формуле y' (0.9;0.1) =1/0.2(0.343 -40.512 + 30.729)= 2.41.

Тот же результат.