24) Радиально-сферический поток. Степень и характер вскрытия пласта.

Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.

Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта. Пример: когда скважина вскрывает только плоскую горизонтальную непроницаемую кровлю.

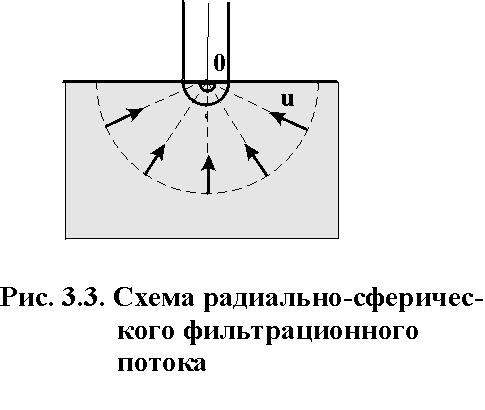
Характер и степень вскрытия пласта.

25) Решение общего дифференциального уравнения установившегося потока. Показатель формы потока.

При условии вытеснения флюида из пласта или его нагнетания в пласт через галерею или скважину условимся принимать за координату произвольной точки пласта расстояние r до этой точки от:

1. галереи (для прямолинейно- параллельного потока);

2. центра контура скважины в основной плоскости (плоскости подошвы пласта) фильтрации (для плоско-радиального потока);

3. центра полусферического забоя скважины (для сферически-радиального потока).

Из условия неразрывности потока:

G-массовый дебит; F_(r)-площадь поверхности равного Р.

26) Величины площади для различных видов одномерных потока. Дифференциальное уравнение потенциального одномерного потока.

1) Прямолинейно-параллельный:

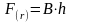
2) плоско- радиальный:

3)радиально- сферический:

Дифференциальное уровнение одномерного потока:

А- коэффициент

dϕ- диф. потенциала

dr- диф. радиуса

r^j-радиус до точки j.

Величины:

1)A=Bh j=0

2)A=2πh j=1

3)A=2π j=2

27) Определение значения массового дебита при известных значениях потенциалов на граничных поверхностях пласт. Отличие массового и объемного дебита.

Проинтегрируем выражение:

Получим:

Для плоско- параллельного найдем единое решение с соответствием с заданными условиями(граничными)

1. известный массовый дебит и значения потенциалов на одном из граничных поверхностях:

2. известны значения потенциалов на двухграничных поверхностях пласта в забое скважины и контуре питания:

Отличие массового и объемного дебита.