§8. Нормальное распределение

С.в. называется нормально распределённой, если плотность вероятностей имеет вид

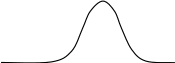
График имеет форму «колокола» - симметричной кривой (рис.4), которую называют нормальной кривой или кривой Гаусса. Расчёты показывают, что

, т.е. параметр - это среднее значение с.в. , а параметр -её среднее квадратическое отклонение. Поэтому, прямая является

осью симметрии графика, а характеризует степень «крутизны» или «пологости» графика.

На рисунке 5 изображены графики двух нормальных распределений.

Y

0 а х

Рис. 4

35

у которых математическое ожидание одинаково, но у второго графика среднее квадратическое отклонение больше, чем у первого, т.е. и, поэтому, график является более «пологим», чем . Y Это означает, что с.в. , плотность распределения которой , является более рассеянной относительно центра распределения (математического ожидания), чем с.в. , имеющая плотность распределения вероятностей . Заметим, что при любых и 0 площадь под нормальной кривой Рис. 5 равна 1. Тот факт, что с.в. имеет

нормальное распределение с параметрами и коротко записывается так: .

Вероятность попадания нормально распределённой с.в. в заданный интервал (α; β) находится по формуле

Ф Ф , (8.1)

где Ф - функция Лапласа, значения которой находятся

по таблице.

Свойства Ф :

1. Ф (0) = 0;

2. Ф (х) – возрастающая функция;

3. Ф (x) 0,5 и Ф (x) = 0,5 ;

4. Ф (-x) = - Ф (x).

Следующее равенство, вытекающее из (8.1), позволяет вычислить вероятность того, что отклонение нормально распределённой с.в. от своего среднего значения не превосходит заданной величины. Если , то

36

Ф (8.2)