7.3. Имитационное моделирование происшествий в человекомашинной системе

Приемлемость метода имитационного моделирования для сис-|много ^следования аварийности и травматизма, как и других

гересующих нас опасных процессов в техносфере, может быть эоснована по меньшей мере следующими двумя основными со-эражениями. Во-первых, выполнение большинства технологичес-операций удобно рассматривать в виде процесса функциони-эвания человекомашинных систем; при этом успешное или не-Ьпешное завершение какой-либо из них будет случайным ис-эдом — появлением или непоявлением происшествий по окон-ании работы этой сложной системы.

Во-вторых, если рассматривать конкретную производственную технологическую операцию, многократно выполняемую на

тачных объектах промышленности и транспорта, то можно ут-Ьрждать и о массовом характере рассматриваемых работ. Следова-

тьно, требования к массовости и стохастичности результатов

1кционирования соответствующих систем на разных объектах

элюдаются, что позволяет использовать метод имитационного эделирования для исследования аварийности и травматизма в (жносфере.

С целью реализации одного из принципов имитационного мо-

елирования процесса появления происшествий, основанного на

Усмотренной семантической модели, проведена ее дальнейшая

эрмализация. В частности, на рис. 7.3 процесс возникновения

198

199

КИНЕЯ0<ЗИ1ГЭ1ЛЖ ОЛОННОИПВХИИИ И^ХИЭО ^Ч1ЭЭ 'Z'l

Иг-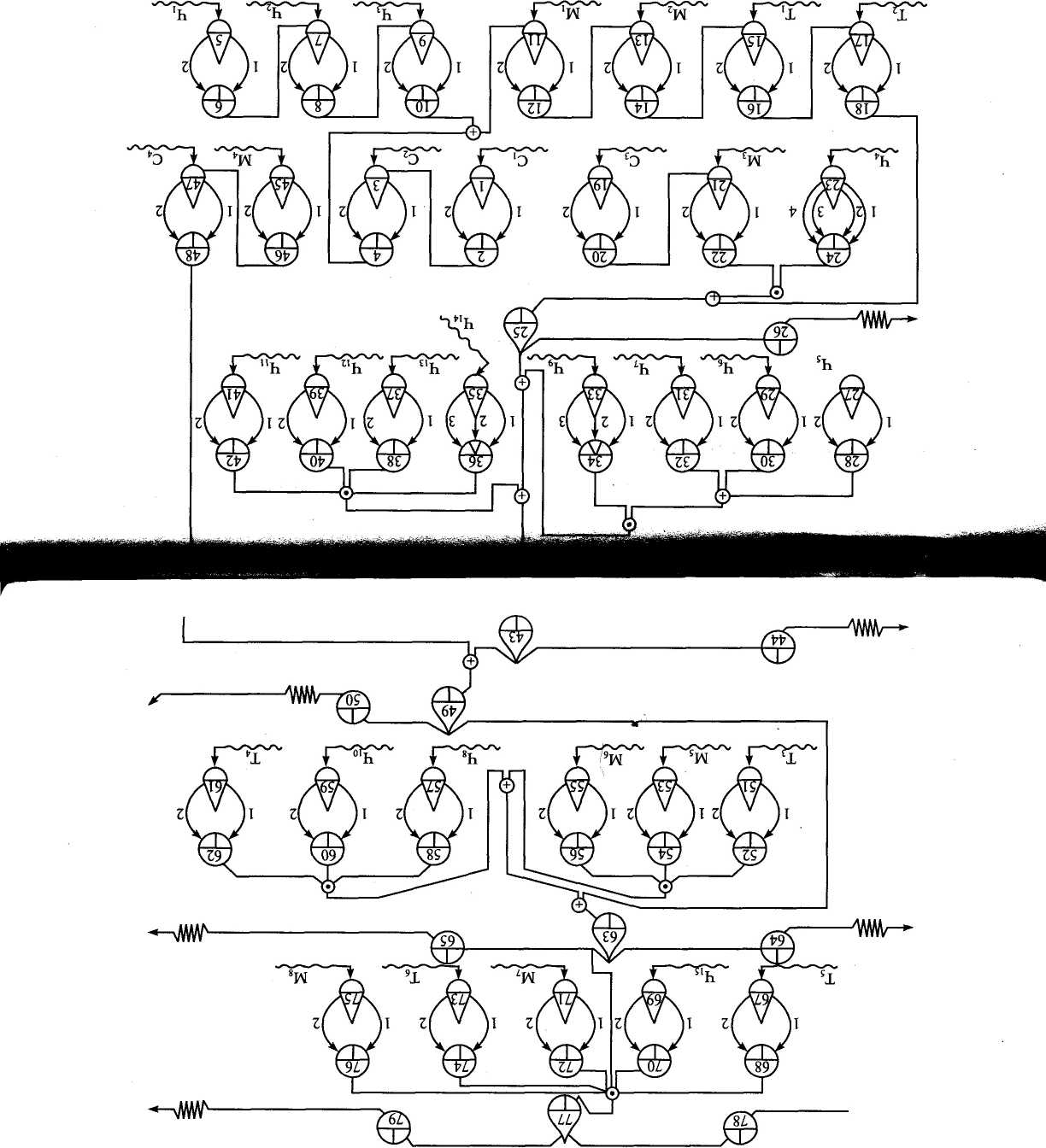

о о

соответствующих предпосылок и перерастания их в причинную цепь аварийности и травматизма представлен уже в виде «чистой» сети GERT, содержащей ветви из неоднократно используемых ранее символов — узлов и дуг, а также некоторых новых элементов.

До того как детально охарактеризовать данную сеть, пояс­ним, что в построенном на ее основе машинном алгоритме все узлы и дуги будут определять условия генерирования, обработки и передачи потока некоторой цифровой информации, указыва­ющей на вклад учитываемых факторов в моделируемый процесс. Для удобства же использования этой модели соответствующие источники такой информации (генераторы случайных чисел, представляющие свойства человекомашинной системы) поме­чены на данном рисунке волнистыми стрелками, входящими в соответствующие узлы, а все эти и другие узлы рассматриваемой сети и некоторые дуги — цифрами, часть из которых уже исполь­зована на рис. 7.2.

Поясним взаимосвязь между элементами двух последних ри­сунков, для чего вначале отметим, что все узлы последней диаг­раммы влияния имеют одинаковые (единичные) степени свобо­ды для первой и последующих реализаций. Затем охарактеризуем другие ее основные элементы и рассмотрим исходные данные, используемые при имитационном моделировании изображенного на этих двух иллюстрациях опасного процесса.

Что касается соответствия между рассматриваемыми моделя­ми, то обратим внимание вот на что. Стохастические узлы сети GERT (см. рис. 7.3), промаркированные цифрами 23, 33, 35 и со­держащие более двух выходных дуг, соответствуют на рис. 7.2 сле­дующему: а) действию человека по восприятию и дешифровке информации о состоянии человекомашинной системны; б) его ре­шению на устранение нарушенного в ней равновесия й в) реали­зованному затем действию. Детерминистские же узлы-статисти­ки, имеющие номера 26, 44, 50, 64, 65, 78 и 79, эквивалентны там событиям в затемненной рамке, а исходящие из них спирале­видные стрелки указывают на возможность регистрации их дости­жения в ходе машинного эксперимента.

Исходными данными, необходимыми для имитационного мо­делирования аварийности и травматизма в техносфере, служат: а) набор тех свойств человекомашинных систем, которые наибо­лее существенно влияют на появление происшествий в техносфе­ре; б) оценки качества каждого такого фактора, варьируемые пе­ред началом проведения машинного эксперимента; в) степень зна­чимости или предрасположенность конкретных свойств к аварий­ности и травматизму в техносфере. Последовательно поясним спо­собы обоснования и оценки параметров перечисленных выше ис­ходных данных, а также укажем порядок их представления в алго­ритме имитационного моделирования.

202

Состав факторов аварийности и травматизма, учитываемых в эдели (рис. 7.2), а затем включенных в сеть GERT (рис. 7.3) и в згоритм имитационного моделирования, установлен по резуль-ам проведенного ранее анализа статистических данных (см. рис. ). Распределение же качества учитываемых здесь свойств чело-екомашинной системы будет задаваться при последующем моде-фовании либо плотностями вероятности этих случайных факто-^(К), либо функциями принадлежности лингвистических пе­ненных ^(К), аппроксимированными тем универсальным спо-

1, который представлен в табл. 7.2. В этой таблице указано одно из довольно распространенных эответствий между количественными (дискретными на отрез-[0, 1]) и лингвистическими (балльными) оценками качества ) свойств сложных систем, учитываемых при их моделирова-I. В ней есть и привычные для четырехбалльной шкалы оценки: тлично», «хорошо», «удовлетворительно» и «плохо». А вот воз-|ожностное и вероятностное распределения оценок качества учи-тваемых факторов показаны на рис. 7.4 в виде графиков: а) фун-1И принадлежности п_х(К), аппроксимированной так называе-

Таблица 7.2

Лингвистические и цифровые параметры функций принадлежности на шкале качества

			Лингвистическая				переменная
	я										Я
		ь^		2				оо Ъ4		о
Количественная	низке	зкое (	е(КЗ)	цнего	о	щего i	ге(К7	ошее (	а	окое (	о о а го
оценка	ь, очень	чень ни	Низко	иже ере	1 а. и	О. О	Хорош	ень хор	й о и 3 га	ень вые	очень
	ж а) В1	О		X		«		О		О	_а Ж (U
	О
											О
	0,08	0,17	0,25	0,33	0,41	0,5	0,58	0,66	0,75	0,83	0,92
(плохо)	0,3	0,7	1,0	0,7	0,3	0	0	0	0	0	0
(удовлетвори-	0	0	0,3	0,7	1,0	0,7	0,3	0	0	0	0
рьно)
(хорошо)	0	0	0	0	0,3	0,7	1,0	0,7	0,3	0	0
(отлично)	0	0	0	0	0	0	0,3	0,7	1,0	0,7	0,3

203

мой L—R формой [16], и б) равномерно распределенной плот­ности вероятности f_x(K).

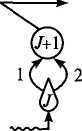
На рис. 7.4 (слева) представлен также один из элементов рас­сматриваемой сети GERT и наиболее общий способ лингвисти­ческой аппроксимации функций принадлежности (формула для 7i_x(K) — над графиками). Для показанного здесь треугольного рас­пределения этой функции справедливо следующее аналитическое выражение:

ась введением так называемого индекса потенциальной опас-рости. Его величина У, пропорциональна частоте повторяемости Ьответствующего фактора аварийности и травматизма (см. про-Ьнтное распределение на рис. 3.4). Значения всех этих индексов Приведены в табл. 7.3, совместно с кодами и наименованиями

читываемых при моделировании свойств человекомашинной си-

~емы.

К-а

т-а

Р-к.

(3-т

= я_х(К) =

; Ке[а,т];

;Ке[/и,р].

(7.18)

Таблица 7.3 Состав и характеристика учитываемых факторов

Номер

узла

где К — уровень качества моделируемого фактора, оцененный баллами соответствующей универсальной шкалы; т — модальное значение этой лингвистической оценки качества; аир — коэф­фициенты размаха ветвей функции принадлежности.

Наконец, относительная предрасположенность к происшестви­ям конкретного свойства человекомашинной системы учитыва-

1. Моделируемое

свойство (фактор аварий­ности и травма­тизма)

2. Принцип имитации предрасположенности к происшествиям

U. 0J. Ц)|. (V7. Ю.

_ __ __ __ __ ___

КГ К2'КЗ'К4' К5' Кб' К7' К8' К9' К10' К11

0,75 0,50

0,25 0,00

На обработку

[0_. ^Пх [КГ

			\	- 4	|К Варьируемая i оценка
		(а)	я^К	-чу 1	\ ^	laicjopa —		к
ч				J	1	k
ч				/11111

От генератора случайных чисел ₀ 0,08 0,17 0,25 0,33 0,41 0,5 0,58 0,66 0,75 0,83 0,92

Количествен­ные и линг-

1зкое

г

S

8

(D О

сокое

Уровень качества

вистические значения

;нь ш

низке

U о

1 о.

днее

редне

ошее

«эрош

окое

ВЫСОК

-нь вы

моде­лируе­мого

качества исследуемых свойств (факторов)

Очень, оч(

Очень

Я

Ниже с

Сре

Выше с

I

Очень з

Вые

Очень

Очень, оче

фактора на выб­ранной шкале

Рис. 7.4. Иллюстрация механизма имитационного моделирования

1*0

I^е:

С

ч₇

Наименование моделируемых факторов

Комфортность среды по физико-химическим параметрам

Качество информационной модели состояния среды

Возможность неблагоприятных воздействий среды на систему

Возможность нерасчетных внешних воз­действий на систему

Н аличие практических навыков выпол­нения операции

Знание технологии работ на данном обору-

довании

Пригодность по психофизиологическим

показателям

Восприятие и дешифровка информации о состоянии системы

Оперативность мышления человека-опе­ратора

Знание порядка действий в нестандартных :итуациях

Способность прогнозировать последствия своих решений

Технологическая дисциплинированность Качество принятия решения

Знание опасных факторов выполняемой операции

19

47

2 3

27

29

31

57 33 59

О

20

48

10

24

28

30

32

58 34 60

Индекс, 1

lvO 2vO lvO 2vO

lvO 2vO lvO

1v2v3vO lvO lvO lvO

2vO

lv2vO

lvO

204

205

			Окончание		табл. 7.3
			Номер
s			узла
о с 1	Код	Наименование моделируемых факторов	Исток	Сток	Индекс, Ij
	4,,	Осведомленность о последствиях	41	42	lvO
		аварийных ситуаций
	4,2	Знание порядка действий в аварийных	39	40	lvO
		ситуациях
	4,з	Обученность действиям в аварийных	38	38	2vO
о 5		ситуациях
	4,4	Точность действий по ликвидации	35	36	2vlvO
		аварийных ситуаций
	4,5	Безошибочность действий в критических	69	70	2vO
		ситуациях
	М,	Качество конструкции рабочего места	11	12	lvO
		человека-оператора
	М2	Степень учета особенностей	13	14	2vO
		работоспособности человека
	М3	Безотказность контрольно-измерительных	21	22	lvO
		приборов
я	М4	Энергоемкость источников опасных	45	46	2vO
X К		техногенных факторов
	м5	Безотказность элементов, удерживающих	53	54	2vO
		опасные факторы
	м6	Длительность действия опасных	55	56	lvO
		производственных факторов	«
	м7	Уровень потенциала опасных	71	72	lvO
		производственных факторов
	м8	Безотказность технических средств защиты	75	76	2vO
		и приборов безопасности
	т,	Удобство подготовки и выполнения работ	15	16	lvO
		на технике
	т2	Удобство технического обслуживания и	17	18	2vO
		ремонта оборудования
ts S	Тз	Сложность алгоритмов функционирования	51	52	lvO
О		человека-оператора
о	т4	Возможность появления персонала в	61	62	lvO
		опасной зоне
	т5	Возможность появления там других	67	68	lvO
		незащищенных элементов
	т6	Надежность организационно-технических	73	74	2vO
		средств обеспечения безопасности

206

..Сущность же механизма, предложенного здесь для имитацион-|ого моделирования происшествий при функционировании че-эвекомашинной системы, состоит в следующем. Генераторы слу-

1ных чисел, построенные на аппроксимации функций /_Х(К) и

(К) равномерно или треугольно распределенными случайными

гачинами (см. рис. 7.4), выдают при опросе случайные числа,

горые имеют вполне определенную корреляцию с индексами 7,-енциальной опасности учитываемых факторов. В частности, чем fee оценка качества К_у соответствующего свойства человекома-

1нной системы, тем более вероятно принятие эти числом наи-эльшего значения индекса (см. правую колонку табл. 7.3).

Количество таких генераторов соответствует числу учитывае-

ых факторов, а выбранные значения индексов 7, их потенциаль-

|ой опасности могут имитировать, как уже указывалось, пред-

асположенность конкретных свойств к формированию предпо-

пюк. В свою очередь, и вся стохастическая сеть будет характери-эвать возможность появления в человекомашинной системе при­чиной цепи техногенного происшествия. В самом деле, если ка-

dtbo ее компонентов имеет низкие оценки, то имитирующие их рнераторы чаще будут выдавать максимальные значения соответ-

вующих случайных чисел.

Нетрудно догадаться, что после обработки логическими узла-значений этих чисел (индексов Ij), будет изменяться и сум-арный индекс потенциальной опасности исследуемого процесса £. Его величина будет определяться как случайно выбранными в энкретной реализации значениями отдельных Ij, так логикой их тожения и перемножения, заданной соответствующими узлами I, представленной на рис. 7.3. Полученная таким образом вели-

т 1_Т может свидетельствовать о предрасположенности к пре­дшествиям рассматриваемого процесса, оцениваемой мерами воз-эжности (вероятностями) возникновения в системе возмуще-

1, опасных и критических ситуаций.

Последнее объясняется тем, что случайная величина 1%, ими-

эующая процесс появления предпосылок к техногенному про-гшествию, способна (как, впрочем, и их причинная цепь) не ько расти, но и уменьшаться. Например, ее увеличение (рост будет иметь место после объединения логическим условием

ш» поступающих на его вход случайных чисел. Допустим, при |гебраическом сложении соответствующего вклада первых из ^вяти факторов, включенных в стохастическую сеть (узлов 1 — 18 " рис. 7.3): С, и С₂, Ч,-Ч₃, M^MjH Т_ь Т₂.

И напротив, исчезновение (или обрыв) причинной цепи пред-

:ылок будет интерпретироваться в том случае, если хотя бы один If инцидентных логическому условию «И» генераторов случайных рсел выдаст нулевое значение индекса I/. Например, такой обрыв

штся, когда узлы 23 — 24 этой же сети сымитируют безошибоч-

207

ное восприятие и дешифровку информации оператором (фактор Ч₄), несмотря на ненулевые значения индексов /₁₉ и /₂₁.

Вот почему величина накопленного индекса опасности может изменяться и имитировать, например, создание условий, необхо­димых и достаточных для появления возмущений, а затем и других нестандартных ситуаций в системе. Следовательно, соответствую­щая машинная реализация конкретной работы будет сопровождаться регистрацией событий, помеченных в правой части рис. 7.3 исходя­щими из них волнистыми стрелками. Это означает, что в человеко-машинной системе возникла опасная и критическая ситуации,, т. е. поток цифровой информации достиг узлов 50 и 65.

Если же значение I_z не превысит некоторых предельных значе­ний, то в системе могут регистрироваться состояния гомеостази-са или адаптации к имевшим место особым ситуациям — дости­жение узлов 26, 44, 64 и 78, показанных таким же способом в левой части сети. В отдельных имитациях исследуемой операции после регистрации опасной и критической ситуации, а затем и дальнейшего повышения суммарного индекса накопленной опас­ности машинная реализация завершится уже фиксацией техно­генного происшествия — одного из событий 79а, 196 или 19в, помеченных волнистыми стрелками в верхней части рис. 7.3.

Данный алгоритм логико-лингвистического моделирования процесса зарождения и развития причинной цепи происшествий в человекомашиннои системе реализован в виде соответствующей экспертной системы (программного комплекса), краткое описа­ние которого приведено в приложении П.7. Использование этой компьютерной программы в целях имитационного моделирова­ния техногенных происшествий позволяет решать следующие три исследовательские и практические задачи:

а) выявлять среди рассматриваемых свойств чедовекомашин- ных систем наиболее существенные факторы аварийности и трав­ матизма;

б) проводить сравнительную оценку безопасности выполнения аналогичных производственных или технологических операций;

в) оценивать эффективность различных организационно-тех­ нических мероприятий по повышению безопасности производ­ ства и транспорта.

Для решения каждой из трех указанных выше задач системного анализа аварийности и травматизма методом имитационного мо­делирования необходимо не менее двух машинных эксперимен­тов, отличающихся следующими исходными данными. Для вто­рой (помеченной буквой «б») задачи — оценками качества соот­ветствующих компонентов аналогичных по составу человекома-шинных систем, функционирующих с целью выполнения одной и той же операции на однотипных образцах технологического обо­рудования. Для первой и третьей задач — различными оценками

208

ачества одной и той же системы, зарегистрированными до и после еализации конкретных организационно-технических мероприя-1Й по повышению безопасности исследуемых работ в техносфере. | Если охарактеризовать машинные эксперименты, то каждый них включает в зависимости от реально наблюдаемой частоты |сследуемых событий и требуемой точности оценки их вероятно-гй несколько тысяч или десятков тысяч имитаций конкретной эизводственной операции. По результатам же проведения от-чьного эксперимента рассчитываются характеристики:

Вероятности появления событий:

динамического равновесия (гомеостазиса) Р₂₆

адаптации к возмущению (адаптации 1) Р44

опасной ситуации Р₅₀

адаптации 2 (к опасной ситуации) Р_м

критической ситуации Р^₅

адаптации 3 (к критической ситуации) Р_п

происшествия Р₇₉

Числовые характеристики распределения:

математическое ожидание М[Д МОЖ

стандартное отклонение о,- СО

наименьшее значение /_Zmin MIN

наибольшее значение I_Zmax МАХ

А вот параметры отдельного машинного эксперимента, свиде-эщие о продолжительности и точности имитационного моде-фования (числе опросов всех генераторов случайных чисел и зна-ении дисперсии сделанных при этом оценок), указаны в табл. 7.4.

Таблица 7.4