Глава 6

Моделирование и системный анализ

Происшествий с помощью диаграмм

Типа «граф»

Вторым (после деревьев) типом диаграмм причинно-следствен­ных связей являются графы, среди которых обычно выделяют два их типа: а) графы переходов и состояний; б) потоковые графы. Продемонстрируем возможности использования этих диаграмм влияния для исследования аварийности и травматизма на произ­водстве и транспорте. Целью же изучения материала данной главы служит уяснение особенностей применения подобных моделей для нужд моделирования и системного анализа процесса возникнове­ния и предупреждения техногенных происшествий.

6.1. Граф-модель аварийности и травматизма

Наиболее представленными в литературе и первыми среди ис­пользуемых для исследования безопасности моделей оказались диаграммы влияния типа «граф». Их достоинство состоит в удоб­стве перехода к знаковым моделям и вывода на их основе матема­тических формул, устанавливающих зависимости между выбран­ными ранее (см. разд. 3.8) количественными показателями без­опасности и основными параметрами человекомашинных систем. Полученные таким образом аналитические выражения могут быть использованы затем для априорной (предварительной) и апосте­риорной (статистической) оценки уровня безопасности технос-ферных процессов.

Проиллюстрируем, как это делается, на примере разработки модели процесса возникновения происшествий при функциони­ровании некоторого производственного объекта. При этом огра­ничимся минимально необходимым числом наиболее существен­ных свойств и параметров рассматриваемого процесса. Поэтому в качестве изменяющихся во времени учитываемых факторов ава­рийности и травматизма ниже будут учитываться только ошибоч-

156

/24(0 ч		Q0)
4»	рщ	5«	"пр

Р ис. 6.1. Граф-модель возникновения происшествий

.ie действия персонала и отказы используемого им технологи­ческого оборудования, которые в совокупности с параметрами эоизводственного процесса и будут включены в разрабатывае-ую модель.

Условия возникновения аварийности и травматизма при вы­полнении в техносфере подобного процесса (работ по эксплуата-*и технологического оборудования) могут быть представлены, например, графом динамической системы, показанной на рис. 6.1. 1а вход такой системы поступает сигнал в виде предполагаемого тотока требований на выполнение к-х производственных опера­ций, задаваемый параметром — оо£^р(/). Значения параметра этого юток| в каждый дискретный момент времени / будут различны-так как определяются переменными во времени числом т вставляющих их технологических операций к-то типа и интен-ривностью выполнения каждой из них X^it).

Возникновение же техногенных происшествий при реализации рассматриваемого процесса интерпретируется соответствующими тайными событиями на выходе граф-модели, учитываемыми араметром потока происшествий — со_пр(О- Считается также, что Появлению каждого такого события предшествуют так называе­мые «особые ситуации», обусловленные сочетаниями случайно эзникших факторов и требующие нестандартной реакции со сто-эны персонала или эксплуатируемого им оборудования. В после-эщем такие ситуации в системе «человек—машина*» будут свя­зываться с возникновением лишь двух типов предпосылок к ава-^рийности и травматизму — ошибок персонала и отказов техники.

О тсутствие в данной системе «среды» как третьего компонента означает, *что в последующем будут игнорироваться предпосылки типа «нерасчетное внеш-|нее воздействие».

157

Преимущественное внимание при этом уделяется появлению «опасных отказов» системы, под которыми ниже подразумевают­ся лишь те ошибки работающих и отказы используемого ими обо­рудования, которые приводят к появлению техногенно-производ-ственных опасностей в зоне действия не защищенных от них эле­ментов системы и ее окружения. Предупреждение таких отказов и ослабление их нежелательных последствий обеспечивается на прак­тике путем адаптации рассматриваемой системы с помощью спе­циально предусмотренных для этого средств и организационно-технических мероприятий. Однако вследствие их несовершенства незамеченные или своевременно неустраненные опасные отказы системы могут привести к появлению опасных и критических си­туаций, а иногда — и к происшествиям.

При построении показанной на рис. 6.1 модели использовались выявленные ранее закономерности аварийности и травматизма, а также упрощающие допущения, позволившие сократить число воз­можных состояний исследуемого опасного процесса и соответ­ствующего ему графа. В частности, в нем непосредственно не учи­тывались нерасчетные внешние воздействия на людей и техноло­гическое оборудование со стороны окружающей среды и специ­ально не обозначались условия выхода человекомашинной систе­мы из опасных и критических ситуаций. При этом предполага­лось, что в случае успешного (в смысле отсутствия происшествий) завершения конкретной производственной операции функциони­рование этой системы прекращалось в одном из подобных «по­глощающих» состояний графа 1, 4 и 5.

Изложенное выше проблемно-ориентированное описание дан­ной задачи отражено тем, что в рассматриваемом здесь графе уч­тены лишь пять состояний, через которые может проходить сис­тема «человек—машина» в процессе своего функционирования, с целью выполнения конкретных технологических операций. Вот их коды и наименования: 1 — динамическое равновесие, характе­ризуемое завершением операций без появления ошибок людей и отказов техники; 2 и 3 — особые ситуации, вызванные возникно­вением соответственно указанных выше ошибок и отказов; 4 — опасное состояние, обусловленное появлением в системе опас­ных отказов, 5 — критическая ситуация, связанная с совмещени­ем зоны действия возникшей опасности и незащищенных от нее компонентов системы.

Сам же процесс возникновения происшествий в ходе рассмат­риваемых работ интерпретируется данной граф-моделью как об­работка потока поступающих на ее вход требований с поглоще­нием части возможных опасных отказов человекомашинной сис­темы в состояниях 4 или 5. При этом не исключается, что реализа­ция отдельных требований может завершаться появлением собы­тий на выходе графа, а количественная мера возможности таких

158

додов характеризуется вероятностью Q(t) появления происше-йий в данный дискретный момент функционирования этой си-емы.

И напротив, завершение технологической операции в состоя-__: 4 и 5 означает, что система «человек—машина» как бы адап-ровалась соответственно к возникшей опасной и критической .уациям путем их ликвидации. Кроме этого, считается, что «по-ощение» конкретного требования на проведение технологичес-операции в любом из этих двух состояний, равно как и в оянии 1, является основанием для начала обработки следую-|ей заявки на выполнение конкретных работ. Принятые при формализации исследуемого процесса допуще-я позволили ограничиться внутри графа всего девятью перехо-~»ш. Этого удалось достигнуть с помощью следующих достаточно равдоподобных предположений: а) исключение прямых перехо­дов из состояния 1 в состояние 5, минуя 4, и в состояние 4, |инуя состояния 2 или 3; б) учет обратных переходов из состоя-...I 2 и 3 в состояние 1, т.е. необходимости повторения операций осле выявления ошибок и отказов; в) возможность взаимно обус-овленных особых ситуаций, т. е. переходов внутри и между состоя-лми 2 и 3.

Анализ природы заявок на выполнение к-х технологических [юраций показывает, что значительная их часть образует пото-л, состоящие из случайных событий, обладающих свойствами рдинарности и отсутствия последствия. Это вызвано сложностью ^временных производственных процессов, большим числом со­ставляющих их технологических операций, ограниченной надеж-_£тью и эргономичностью оборудования, возможностью возник-рвения ошибок людей и отказов техники, а также необходимос-Ью последующего устранения таких нестандартных ситуаций.

Приведенные особенности свидетельствуют о возможности ринятия допущения о представлении требований на выполне-т отдельных технологических операций в виде потока случай-'>. событий. По крайне мере, такое (не принципиальное для пос-ёдующих рассуждений) допущение справедливо в тех случаях, ,эгда исследуемый производственный процесс состоит из боль-аого числа операций сравнительно малой интенсивности, а не-эторые из них имеют даже явно выраженный регулярный харак-ер.

Принятое допущение применено ниже при выборе способа 1ределения вероятности Q(t) и параметра со_пр(0, указывающих 1 возможность и частоту появления техногенных происшествий, ^ля этого было использовано свойство инвариантности (неизмен­ности основных характеристик) простейшего потока после его азряжения, путем исключения отдельных событий с вероятнос-ью 1 - Q(t). Данное свойство подтверждается выявленным ранее

159

(см. разд. 3.2) пуассоновским распределением числа моделируе­мых здесь событий при проведении производственных процессов. Аналитическое выражение оператора Q(t) может быть получено в этом случае с помощью тех вероятностей Ру просеивания собы­тий входного потока при их переходе из состояний / е {1, 2, 3, 4} в состояния j e {2, 3, 4, 5} графа, наименования и обозначения которых представлены в табл. 6.1.

Таблица 6.

Вероятности, используемые в граф-модели

Обозна­чение

Наименование

Р,2«)

Вероятность возникновения ошибок персонала при реали­зации им заданных алгоритмов действий в к-й операции

Условная вероятность появления ошибок одного типа (од­них рабочих) при появлении ошибок другого типа (других рабочих)

Условная вероятность возникновения ошибок людей при появлении отказов технологического оборудования

Вероятность своевременного выявления и исправления ошибок персонала

Вероятность появления отказов технологического оборудования при выполнении им заданных функций

Условная вероятность появлений отказов одного типа (од­них элементов) по причине отказа другого типа (других элементов оборудования)

Условная вероятность возникновения отказов оборудования при появлении ошибок персонала

Вероятность своевременного устранения людьми отказов используемой ими техники

Вероятность возникновения «опасных» ошибок персонала Вероятность появления «опасных» отказов оборудования

Условная вероятность перерастания опасной ситуации в критическую

Условная вероятность перерастания критической ситуации в происшествие

Знание же величины Q{t), являющейся дополнением вероят-и выполнения производственного процесса без происшествий (0=1- Q(0> позволит получить такое выражение для парамет-потока происшествий:

ю_Пр(0 = «F(0Q(0- (6-1)

При определении входящего в формулу сомножителя Q{t) не читывается возможность многократного индуцирования особых _уаций. Это значит, что отказ любого из компонентов системы леловек—машина» может вызвать с соответствующей вероят­ностью не более одного последующего отказа техники или од-„эй ошибки персонала. Принятие данного допущения как бы выключает «зацикливание» потоков внутри графа, ограничивая ray цепи предпосылок к особой ситуации двумя такими собы-

дями.

Приемлемость же этого ограничения обоснована на практике энтролем действий работающих на технике людей, а также бло-нровкой или автоматическим отключением оборудования при оявлении там опасных отказов или ошибок. Вследствие этого ве-оятности возникновения третьей и последующих предпосылок удут величинами значительно меньшими по сравнению с вероят-

стями исходных ошибок и отказов.

Согласно принятым предположениям о необходимых и доста-очных для появления техногенных происшествий условиях, мо-

' быть записаны соответственно следующие выражения для па-

летров потока возможных ошибок персонала и отказов исполь-^емой ими техники:

(6.2)

©12(0 со₁₃(0

Подобным образом получаются выражения для параметров эка тех отказов и ошибок, которые индуцированы предше-вующими предпосылками:

(6.3)

«32(0 =

ю₂₂(0 и га₃₃(0 — параметры, учитывающие возможность воз-хновения ошибок и отказов одного типа (одних компонентов иовекомашинной системы) при возникновении ошибок и от-

зов другого типа (других ее элементов) соответственно. Значения последних параметров потока случайных событий

Ьгут быть найдены по следующим зависимостям:

Примечание. Все вероятности определяются для людей и техники, заня­тых в выполнении конкретных работ в дискретный момент времени /.

160

«Шелов

«22(0 = «12(0^22(0; «33(0 = «13(О^ЗЗ(О-

(6.4)

161

После подстановки выражений (6.2) в формулы (6.3) с учетом зависимостей (6.4) и вынесения общего множителя за скобки получим

«2з(0 = «*(0Л₂(0/>2з(0[1 + ^(01;

«32(0 = «*(0Лз(0^32(0и + РззШ- (6-5)

По аналогии с (6.3) запишем выражения для определения ин-тенсивностей исправления ошибок персонала n₂i(0 ^И устранения отказов технологического оборудования — H3i(0; которые (см. вто­рой круг со знаком плюс на рис. 6.1) являются слагаемыми сум­марного параметра потока требований на повторное выполнение к-х производственных операций a>_k(t):

H2l(0 = [«12(0 + «32(0 + «22(0]/⁵2l(0;

= [«в(0 + «2з(0 + СО₃з(0]^31(0- (6.6)

Подстановка выражений (6.2), (6.5) в зависимости (6.6) и не­сложные преобразования дают следующие формулы для опреде­ления искомых составляющих суммарного потока дополнитель­ных требований:

МО =

H3l(0 = C....

Для отыскания параметров потоков своевременно не исправ­ленных ошибок людей — «24(0 ^и своевременно не устраненных отказов используемой ими техники — со₃4(0> образующих при на­ложении поток опасных отказов системы «человек—машина», вве­дем дальнейшие допущения. Будем считать, что процесс развития происшествия происходит практически мгновенно, что позволя­ет рассматривать его модель как безынерционную динамическую систему, исключающую потерю событий в состояниях 2 и 3 рас­сматриваемого графа.

Правомерность этого предположения обоснована малостью времени, требуемого для отдельных технологических операций, и быстротечностью нахождения системы в этих состояниях по срав­нению с длительностью всего производственного процесса. Сле­довательно, с учетом равенства в каждый момент времени пото­ков событий, входящих и выходящих из состояний 2 и 3 графа, можно утверждать о справедливости таких выражений:

«24(0 = «12(0 + «22(0 + «32(0 - «2з(0 ~ H2l(0l

«34(0 = «13(0 + «33(0 + «23(0 - «32(0 - H3l(0- (6-8)

После подстановки в правую часть равенства (6.8) значений его слагаемых и алгебраических преобразований получим следую-

> формулу для параметра результирующего потока опасных си-щй:

«ос(0 = «24(0 + «34(0 = «*(0{Л2(0[1 + ^22(0 ~ Pjlif) ~

/*зз(О -}• (6.9)

ЦС целью исключения из выражения (6.9) неизвестных пара-эов напомним, что параметр потока фактических требований выполнение к-х технологических операций может быть пред-тен в виде такой суммы:

Подстановка в (6.9) значения со*(0, найденного по формуле |Л0) с учетом (6.8), и соответствующие преобразования дают 1едующее выражение для параметра потока происшествий при шолнении производственной операции:

(6.11)

|е Q_k(t) — вероятность возникновения техногенных происше-вий в данный момент времени проведения Jt-й операции, опре-яемая по такой формуле:

= [P_n(t)[l + P₂₂(t) - Pixif) ~

(6.12)

-P₃i(0 - /33W/31W " P^t)Pn(t) - /33(0/32(0/21(0]]/

/[1 - /M0[/2i(0 + /22(0/^1(0 + /^3(0/31(0 + +P22M ■ P₂₃(0/3i(0] - /b(0[/3i(0 + /33(0/31(0 +

+/32(0/21(0+

Следуя рекомендациям разд. 2.3, проведем контроль правиль-эсти, а затем (в следующем параграфе) и анализ полученной 1алитической модели на качественном и количественном уров-1х. Для этого вначале поясним, что в выражении (6.12) пер-1Й сомножитель (дробь) представляет собой вероятность появ-Вния опасных ситуаций, рассчитываемую как сумму вероятно-вй возникновения своевременно невыявленных и/или неуст­анных ошибок людей (ее первое слагаемое) и отказов техни-(второе слагаемое). Тогда как два других сомножителя явля-гя уже соответствующими (см. табл. 6.1) условными вероятно-1ми.

Согласно принятым допущениям, сумма вероятностей jP₁₂(0 ^и ||з(0, стоящих в виде сомножителей перед квадратными скобка-числителя и знаменателя этой дроби, никогда не превышает

162

163

единицы: Лз(О + Лг(О < 1> ^{так как} состояние 1 как бы «погло­щает» часть требований входного потока. Это же справедливо и для вторых сомножителей рассматриваемой дроби (выражений в квадратных скобках), что обусловлено их структурой и размерно­стями входящих в них параметров. Поэтому для всех операций со­временных производственных процессов, характеризуемых значе­ниями вероятностей Р₁₃(0 и Р₁₂(0 « 1, a P_2i(t) и P_3l(t)-*l, величина всей дроби обычно не превышает одной или двух деся­тых от единицы.

Особенно наглядно будет видно, что числитель дроби должен быть всегда меньше знаменателя из полученного ниже выражения (6.23), являющегося частным случаем зависимости (6.12), где это условие соблюдается для всех P_u(t) + Лз(0 < 1-

Контроль правильности полученных выражений указывает на возможность определения вероятности возникновения прои­сшествий при выполнении исследуемых производственных про­цессов в тех случаях, когда известны показатели безотказности и безошибочности занятых в них оборудования и эксплуатиру­ющего его персонала, а также некоторые другие параметры кон­кретных технологических операций и данного процесса в це­лом.

Так, при известном количестве типов составляющих их опера­ций т, предполагаемой интенсивности работ со£^р(/) и найденной с помощью предложенной модели вероятности Q_k(t), уровень без­опасности конкретного производственного процесса может быть оценен такой формулой:

(6.13)

Р_б(х) =

тогда как вероятность возникновения аварийности и травматизма в рассматриваемых условиях будет определяться ее дополнением до единицы:

(6.14)

0(т) = 1-ехр-

Таким образом, моделирование условий появления аварийно­сти и травматизма с помощью потокового графа подтверждает возможность получения аналитических выражений, пригодных для исследования и количественной оценки выбранных ранее показа­телей качества системы обеспечения безопасности. Однако до того, как сформулировать соответствующую методику, целесообразно еще раз проверить только что полученные здесь результаты моде­лирования на достоверность и обосновать возможность получения необходимых исходных данных.

6.2. Обоснование и анализ результатов моделирования

| Ценность любого исследования и полученных в нем результа-определяется, как известно, их достоверностью и возможное -практического использования. Применительно к моделиро-Цнию опасных процессов в техносфере особый интерес име-г: 1) новые либо уточненные представления о закономернос-: возникновения и предупреждения техногенных происшествий; предварительная оценка их параметров на стадии разработки

реконструкции производственных объектов. |^? Укажем способы решения этих двух задач путем: а) обоснова-[ возможности получения исходных данных для формул (6.12) — 5.14); б) проверки степени ее адекватности и достоверности по гношению к другим результатам. При обосновании методов оп-з;еления параметров формулы (6.12) будем исходить из инфор-хии, полученной в ходе разработки производственных процес-эв, а также принятых выше предположений и допущений. Реше-*е же этой задачи начнем с указания способов априорной оцен-: условных вероятностей: Р₄₅(0 и P_np(t) — соответственно появ-бния критических ситуаций и происшествий после возникнове-1я опасных и критических ситуаций, а затем и вероятностей Ру «ены других состояний графа.

Согласно принятому выше определению, наступление крити-:ких ситуаций (достижение состояния графа 5) возможно лишь ри совмещении незащищенных элементов системы «человек— |ашина» и зоны действия возникшей ранее опасности. Следова-ельно, для достоверного отыскания значений вероятности пере-астанрс опасной ситуации в критическую Р₄₅(0 необходимо иметь п-ше о параметрах, характеризующих опасные факторы иссле-уемой человекомашинной системы. В большинстве случаев, од-|ако, можно утверждать, что верхняя оценка величины этой ве-эятности равна

Pisit) = ^т£⁴⁾(0Л*(0) (6.15)

Де т£⁴⁾(0> T/t(O — значения времени возможного нахождения не-ащищенных элементов конкретной человекомашинной системы |зоне возможного действия опасных производственных факторов Достоянии графа 4) и продолжительности к-я операции в диск-гный момент времени / соответственно. Для определения вероятности перерастания критической си-уации в происшествие P_np(t) потребуется детальное исследова-необходимых для этого условий. В первом приближении его эзникновение может быть представлено в виде произведения (а тогда и суммы) таких случайных событий, как отказ техничес-IX средств защиты, предусмотренных на случай опасных ситуа-1й, и (или) ошибка в действиях персонала по ликвидации их

164

165

нежелательных последствий. Считая перечисленные условия не­обходимыми и достаточными для возникновения техногенных происшествий, может быть составлена структурная схема без­опасности функционирования человекомашинной системы при появлении в ней критической ситуации.

На рис. 6.2 изображена одна из таких схем, включающая следу­ющие обозначения: г — число технических средств защиты, за­действованных при выполнении конкретной производственной операции (верхний блок), и v — количество персонала, занятого в ней (нижний блок схемы). В этих условиях перерастание крити­ческой ситуации в происшествие (переход события через состоя­ние графа 5) эквивалентно его пропуску хотя бы одним из блоков структурной схемы. Следовательно, можно записать такое соотно­шение

Лтр(0 = 1 - P_m{t)Pb(t), (6.16)

где P_m(t) — вероятность безотказной работы технических средств защиты в дискретный момент времени t проведения производ­ственной операции, найденная при условии, что к ее началу они были исправны; P₅(t) — вероятность безошибочного выполнения персоналом тех алгоритмов действий, которые предусмотрены на случай возникновения критической ситуации (состояние 5), рас­считываемая при аналогичных условиях.

Рис. 6.2. Структурная схема безопасности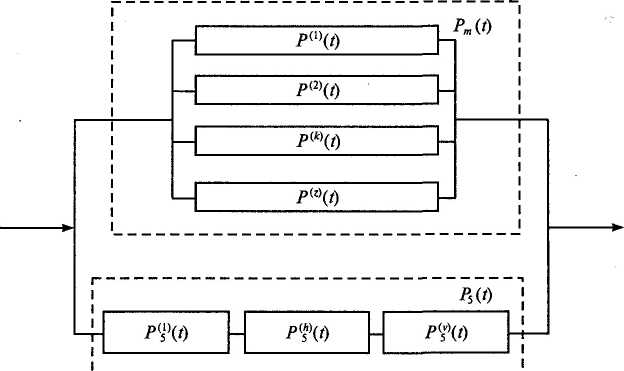

Значение входящей в формулу (6.16) вероятности P_m(f) может быть определено известными методами прогноза показателей на­дежности в технике — с помощью вероятностей безотказной ра­боты отдельных (к-х) технологических средств обеспечения без-

|асности P^\t), их общего количества г и способа соединения в руктурной схеме безопасности. Например, для показанного на :. 6.2 параллельного соединения рассматриваемых средств вели-

Ша этой вероятности должна рассчитываться по такой формуле:

(6.17)

ГДа как при последовательном соединении технических и тех-

тогических средств обеспечения безопасности, достаточно пе-имножения Pj®. |' При определении данной вероятности в других случаях необ-

:щмо руководствоваться соответствующими положениями тео-■га надежности. При этом следует учитывать лишь те отказы тех-тческих средств защиты, которые сопровождаются воздействи-

случайно возникших опасных факторов на не защищенные от : элементы техники и части тела человека. Иначе говоря, веро-

■юсти PЈ\f) по отношению к иным отказам средств защиты [»авны единице и здесь не учитываются.

Для предварительной оценки второго сомножителя формулы 3.16) — вероятности P₅(t) необходимы данные о численности v ерсонала и значениях вероятностей P₅^w(t) безошибочного и свое-эемённого выполнения им действий, предусмотренных на слу-ай возникновения критических ситуаций. Значения параметра v перечень подобных нестандартных ситуаций могут быть найде-путем изучения эксплуатационно-технологической докумен-

1ии с учетом имеющегося аналогичного опыта.

В первом приближении будем считать, что значение искомой гроятности безошибочных и своевременных действий персонала

ликвидации возникших критических ситуаций может опреде-яться по следующей формуле:

/Кэ.

э.у>

(6.18)

А=0

це К_э у — коэффициент, используемый для учета степени экст-вмальности либо дискомфортности условий труда на рабочем человека-оператора. Его значения могут быть найдены в

этветствующей в литературе по эргономике либо с помощью

5л. П. 1.2.

Величина входящей в эту формулу вероятности безошибочных \ своевременных действий человека P^^h\t), а также имеющиеся в одели (6.12) вероятности выполнения других подобных действий:

i (0 — по ликвидации ошибок, замеченных им при реализации шных алгоритмов выполнения k-Vi работы, и -P₃i(0 — по свое-

еменному устранения возникших там же отказов технологичес-Ьто оборудования, равно как и P_n(t) — вероятности возникно-

166

167

вения ошибок персонала, могут быть определены с помощью обоб­щенного структурного метода теории эрготехнических систем [15].

Исходными данными, необходимыми для предварительной оцен­ки перечисленных выше показателей безошибочности и своевре­менности действий человека, служат предусмотренные технологи­ей работ и заданные соответствующей документацией: а) алгорит­мы Ар функционирования персонала в различных (стандартных / = 1 и нестандартных / = 2, 3, 4, 5) ситуациях; б) справочные данные о продолжительностях, вероятностях безошибочного вы­полнения среднестатистическим человеком элементарных действий на технике; в) перечень подобных действий (тактов алгоритма Ар) и те их количественные параметры, которые требуются для оценки интересующих нас вероятностей (см. табл. П. 1.1 —1.4).

В частности, расчет вероятности своевременного выполнения человеком возложенных на него функций за заданное время Pf,^h)(A⁽;\ т_д°), (/ = 2, 3) основан на аппроксимации ее значения га'мма-распределенной случайной величиной, характеризуемой следующими параметрами формы и масштаба:

С, = М²[т,]М>²; d, = M[x«j]/a²_t/, (6.19)

где М[т%], о_т, — соответственно математическое ожидание и стан­дартное отклонение времени выполнения человеком алгоритмов, предусмотренных для него в различных ситуациях.

При известных значениях параметров левых частей выражений (6.19) вероятности своевременного устранения возникших отка­зов и ошибок оказываются соответственно равными

Рг\{*) = ^21(4²⁾'^тд^2>) ⁼ 1-Ф(2</2,-с⁽д²\С₂); (6.20)

P_ix(t) = Z$i(/4} >^тд ) = 1-Ф(2^з_!^тд >С₃); (6.21)

где _т(') — предельно допустимые интервалы времени с момента возникновения ошибки (/ = 2) или отказа (/ = 3) до появления опасного фактора; Ф(2</, х_д, Q — функция гамма-распределен-ной случайной величины.

А вот для определения входящих в выражения (6.19) парамет­ров длительности Affx'jj], o^(/)j и безошибочности людей [1 - P_x2{t)] может быть использована такая процедура. Все возложенные на пер­сонал алгоритмы АР декомпозируются на упомянутые выше так­ты, а из их совокупностей затем формируются типовые функцио­нальные структуры. Эти структуры впоследствии свертываются к одной из простейших форм с заранее выведенными расчетными формулами, позволяющими оценить искомые здесь параметры.

Вероятность безотказной работы технологического оборудо­вания за время выполнения к-х производственных операций — [1 - Лз(01 может быть оценена методами теории надежности при предполагаемых интенсивностях его отказов — X(t) и расчетной

168

ельности работ x_k(t). Для сравнительно небольших интерва­ле времени их реализации справедлива такая формула:

Р₁₃(0 = 1-е^х-^т<⁽'>, (6.22)

А., — принятая постоянной в дискретный период х_к= (t₂ - t{) сплуатации производственного оборудования интенсивность его «азов.

Наконец, условные вероятности появления а) ошибок людей j-за отказов используемой ими техники P₃₂(t), б) отказов вслед-вие ошибок P₂i(t), равно как и в) ошибок одного типа (челове-а) из-за ошибок другого P₂₂(t), а также г) отказов одного типа |рдних элементов) вследствие отказов других P₃₃(t), могут быть ы рассмотренными выше методами, но при условии их екоторой модификации.

Так, для оценки условных вероятностей Р₂з(0 ^и Рзз(^{) ^В струк-эные схемы безотказности технологического оборудования дол-ш включаться все его взаимодействующие элементы, а при определении показателей P_i2(t) ^И Рц(() с помощью типовой фун-■гональной структуры алгоритма функционирования — весь пер-энал, участвующий в выполняемой и смежных с нею технологи­ческих операциях. Исследование полученных таким образом диаг-щм влияния, например, методом статистических испытаний юзволит оценить значения указанных вероятностей.

Учитывая трудоемкость определения условных вероятностей СРзгО), Рц{^{), Рзз(О, целесообразно провести некоторое ■цющение формулы (6.12) и выдать рекомендации по дальней-1ему облегчению оценки входящих в нее параметров. Покажем на примере производственных операций простейшего типа, Йыполняемых на отдельном образце технологического оборудо-1ия или на нескольких образцах, но при условии, что один рабочий приступает к действиям лишь по прекращению функ-ш другого.

^Pn{t)

Оказывается, что рассмотренная выше модель может быть зна-ельно упрощена. Легче всего сделать это путем исключения эй графа потоков с параметрами ю₂з(0; ^юз2(0> ^2г(^{)> <°зз(Оэ эквивалентно присваиванию в формуле (6.12) соответствую-ш вероятностям нулевых значений. В этом случае данная фор-ула принимает более обозримый вид:

... (6-23)

Заметим также, что при простейших алгоритмах, показатели

зошибочности и своевременности их выполнения персоналом

эгут быть рассчитаны не по формулам (6.18) —(6.21), а простым

еремножением соответствующих параметров безошибочности эле-

Ентарных действий среднестатистического человека-оператора

169

или сложением длительностей времени их выполнения. Напом­ним, что все эти параметры определяются с помощью справоч­ных данных, в том числе и прилагаемых к данной работе.

При найденных с помощью формул (6.23) или (6.12) значе­ниях Q_k{t) величина параметра потока происшествий определяет­ся таким образом:

(6.24)

/t=0

а вероятность аварийности и травматизма на интервале т = t₂ - Ц будет равна

<2(т) = 1 - ехр - (ш_прт), (6.25)

где го_пр — среднее на рассматриваемом отрезке времени значение параметра потока происшествий, рассчитываемое при усреднен­ных значениях тех учитываемых показателей качества человекома-шинных систем, которые входят в формулы (6.23) или (6.12).

Завершим проверку правильности полученных здесь аналити­ческих моделей путем изучения реакции левых частей выражений (6.12), (6.15) —(6.25) на изменение входящих в их правые части параметров, а затем и проведем ее качественный анализ.

Оказывается, что при нижних и верхних граничных значениях вероятностей P_v(f) и Р_пр(0, равных соответственно нулю и еди­ нице, величина Q_k(t), как это следует из зависимостей (6.12) и (6.23), становится также равной этим крайним значениям. Подоб­ ный эффект проявляется и для вероятности Q(x) в случае приня­ тия в формуле (6.25) нулевых или бесконечно больших значений времени и параметра потока происшествий — та_пр. *

Повышение же интенсивности рассматриваемых работ (рост параметров co]t^p(0 и т), увеличение вероятностей P_l2(t), Лз(0 воз­никновения отказов и ошибок, равно как и снижение числа и эффективности технологических средств обеспечения безопас­ности — рост вероятностей P_np(t) и P₄s(t), способствуют [см. фор­мулы (6.12) и (6.23)] аварийности и травматизму на производ­стве. В то же время безошибочное выполнение персоналом своих функций и безотказное функционирование используемого ими оборудования [Рп(0 = Р_пЬ) = 0], а также безошибочное и своев­ременное устранение указанных предпосылок [P₃i(0 = Pi\(t) = 1] полностью исключают, в соответствии с теми же формулами, по­явление происшествий.

Таким же образом можно констатировать соответствие между разработанной моделью и объективно действующими закономер­ностями аварийности и травматизма на производстве. Некоторые из них, касающиеся реакции Р_б(х) = 1 - £>(т) на изменение веро­ятностей появления Р₎₃(/) и устранения P₃i(0 технических пред-

тосылок к происшествиям, проиллюстрированы на рис. 6.3 гра­фиками, подтверждающими правдоподобность результатов про­веденного выше моделирования.

Отметим, что качественный анализ приведенного на рис. 6.1 эафа и выведенных на его основе зависимостей (6.12), (6.23), тозволяет уточнить содержание таких важных понятий, как «бе-эпасность производственных процессов» и «безопасность произ-эдственного оборудования», а также уточнить соответствующие Эпределения «Системы стандартов безопасности труда». Имеющи-гя там тавтологии типа «безопасность оборудования обеспечива-гся безопасностью его элементов» целесообразно заменить теми юложениями, которые вытекают из рассмотренной выше моде-ш аварийности и травматизма в техносфере.

§0,70

0,60 0,55 0,55 0,45

|0,71

	(1) (	2) (3) 13 > Лз
	\\
Рп Р22	= 0,849 \ = Ргз = 0 = 0,08 = 0,645 = Р32 = 0 = 0,5 = 0,075 1, т= 10 261/год
Рзх Рзз		1	ч
р * пр т =

'0,72

;о,73

В самом деле, более безопасным будет тот процесс, который эй прочих равных условиях имеет простую структуру (малое чис­то т), низкие интенсивность ю£^р(0 и продолжительность т ра-эт, а также совершенные средства обеспечения безопасности — лалые Ptfit) и P_np(t). «Безопасно» же то оборудование, которое эладает простой (а значит, более безотказной) конструкцией — шзкими Puit), P_2i{t) и ^(О — или является эргономичным, т.е. эебует простых алгоритмов и защищено от ошибок персонала в Зычных и нестандартных ситуациях. Поясним, что повышение рргономичности техники обычно проявляется на практике в сни-сении таких вероятностей, как P_l2(t), P₃₂(t), P₂₂{t) и P₅(t). Как уже, видимо, заметил читатель, последние два условия тяются взаимно исключающими друг друга. Данный факт слу-

	(1) (2) (3) Р s P s P *Ъ\ < "31 < "31
		/1;;	= 0,024 = 0,08
			= Лз = 0 = Рзз = 0 = 0,05
		/Я =	= 0,075 = 1, т = 20 = 521 /год

0,012 0,018 0,024 Р₁₂ 0,2 0,4 0,6 0,8 Р_гх

Рис. 6.3. Графики зависимостей />₆ (Р_п\Рц, Р_пр, т) и P₆(P₂il. Рц, Р_пр, х)

170

171

жит еще одним подтверждением тех объективно существующих диалектических противоречий, которые порождают возникнове­ние техногенных происшествий и которые должны учитываться при системном анализе и системном синтезе обеспечения безо­пасности техносферы.