4. Метод наименьших квадратов.

После того как выбрана модель и определен ее вид, следующим шагом является оценка параметров модели. Для линейной парной регрессии вида

необходимо оценить свободный член уравнения регрессии (константу) а и коэффициент регрессии b. Для определения параметров модели можно использовать следующие критерии:

1) сумму квадратов отклонений фактических значений результата у от рассчитанных с помощью уравнения регрессии :

Эта сумма, используется в методе наименьших квадратов, который является одним из основных методов эконометрики;

2) сумму модулей отклонений наблюдаемых значений зависимой переменной у от ее расчетных величин :

3) Сумма, включающая отклонения с определенной мерой,

Где g - мера, с которой отклонение для i-го наблюдения входит в функционал.

При использовании МНК оптимальными будут значения параметров регрессии, минимизирующие функционал S.

Для оценки параметров модели линейной регрессии наиболее часто используется МНК, согласно которому в каче­стве оценок параметров принимают величины а и Ь, минимизирующие сумму квадратов отклонений наблюдаемых значений результативного признака у от расчетных (теоретических)

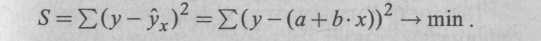
Значения рядов наблюдении х и у нам известны. В функционале S они являются константами, а оценки параметров а и b — переменными. Чтобы найти минимум функции двух переменных, необходимо вычислить ее частные производные по каждому из параметров и приравнять их к нулю (это необходимые условия для экстремума):

Из этих равенств получается система нормальных уравне­ний для оценки параметров а и Ь:

5. Вычисление параметров регрессии и их интерпретация.

Решая данную систему, находим оценки параметров рег­рессии:

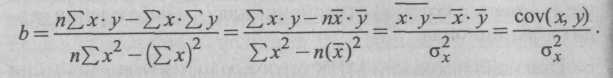
или

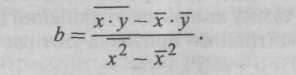
Параметр b называют коэффициентом регрессии. Его величина показывает, насколько в среднем изменяется значение результативного признака при изменении факторного на единицу. Значения параметра b не имеют ограничений. Если коэффициент регрессии больше нуля, то при увеличении фактора результат повышается и линия регрессии является возрастающей. Если же коэффициент регрессии меньше нуля, то при увеличении фактора результат уменьшается и линия регрессии имеет отрицательный наклон.

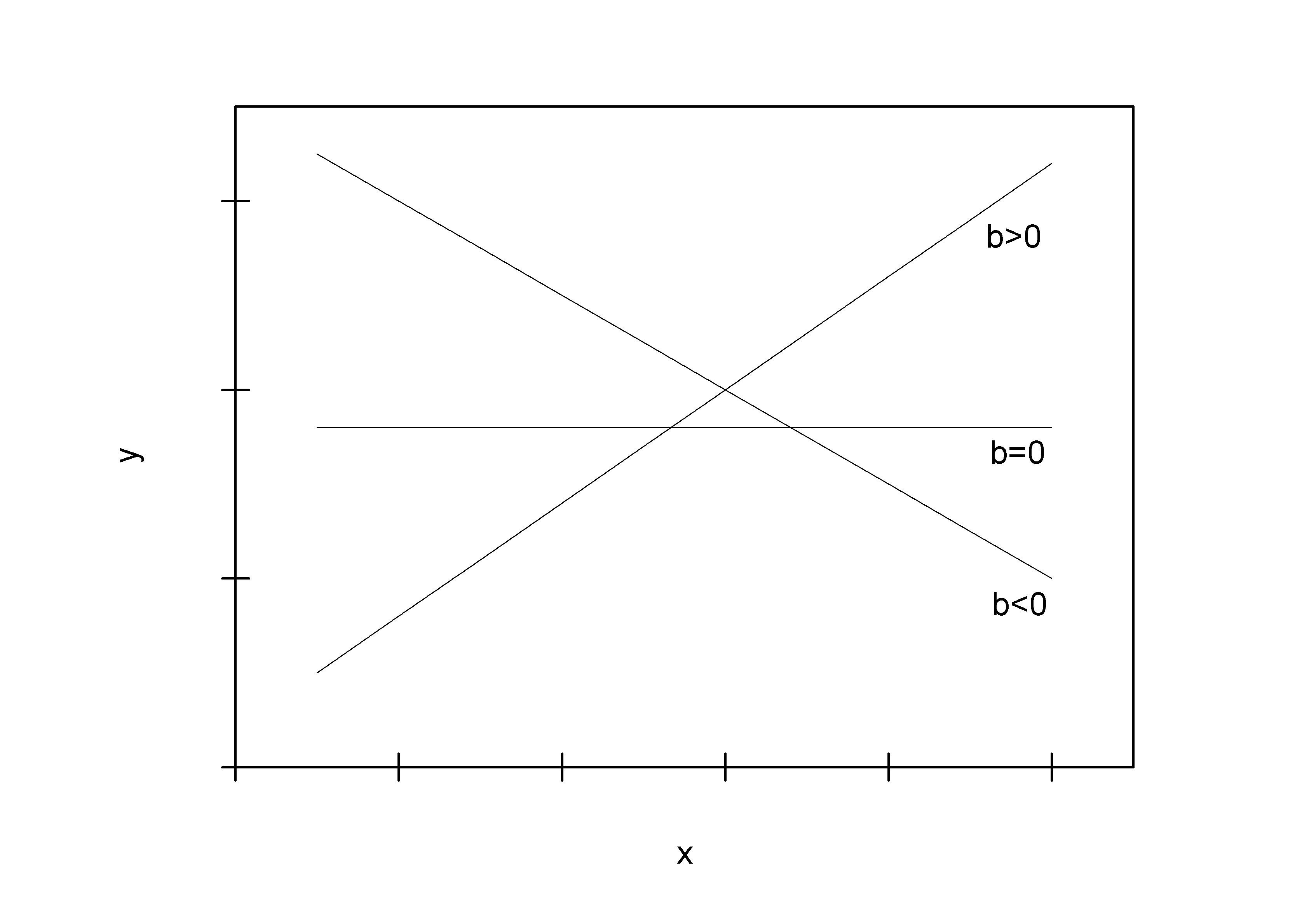
Наклон линии регрессии в зависимости от значения параметра

Параметр а оценивается по следующей формуле:

Рассмотрим, как на практике найти параметры регрессии. Предположим, что по нескольким предприятиям имеются два ряда наблюдений: выпуск продукции и суммы затрат на производство. Зависимость между объемом выпуска и затратами можно представить в виде парной линейной регрессии.

Номер наблюде-ния	Затраты на производство у, тыс.руб.	Объем выпуска х, тыс.ед.	У*Х	Х2	Ух
1	68,8	45,1	3102,88	2034,01	66,68
2	61,2	41,3	2527,56	1705,69	62,61
3	59,9	38,7	2318,13	1497,69	59,82
4	56,7	36,5	2069,55	1332,25	57,46
5	55	36,2	1991	1310,44	57,13
6	54,3	32,4	1759,32	1049,76	53,06
7	49,3	28,1	1385,33	789,61	48,44
Итого	405,2	258,3	15153,77	9719,45	405,20
Среднее значение	57,89	36,90	2164,82	1388,49	57,89

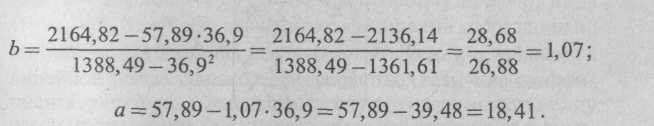
Уравнение регрессии, описывающей зависимость затрат от объема выпуска, будет выглядеть следующим образом:

т.е. при увеличении объема выпускаемой продукции на 1 тыс. ед. затраты на производство возрастут на 1070 руб. По этому уравне­нию рассчитаем теоретические значения результата и сравним полученные суммы:

Из табл. следует, что это равенство выполняется.