Расчёт магнитной системы

Начальный зазор якоря: δ_н= β +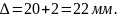

Определим конструктивный фактор

На основе зависимости B_δ от (рис. П3.5 из [2]) находим, что

B_δ=0,2 Тл.

Найдем площади полюса и якоря:

Зададимся размерами магнитопровода:

a= 40 мм; R₀=40 мм; с=3 мм; d_с= 35 мм; h= 28 мм; e=0 мм.

Рис. 7. Основные размеры магнитопровода

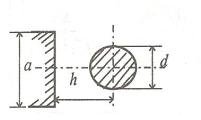
Рис. 8. Дополнительные размеры магнитопровода

Расчёт проводимостей

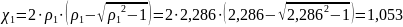
Проводимость зазора:

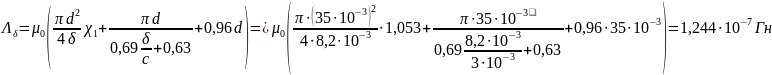
Удельная проводимость рассеяния:

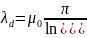
Алгоритм расчета магнитной системы по участкам

Для расчёта магнитной системы методом участков разобьем длину сердечника на n участков и определим удельную МДС f=F/l. Обозначим длины участков как ∆x_i и составим схему замещения магнитной цепи. Введем обозначения:

R_мя - магнитное сопротивление якоря;

R_δΣ – суммарное магнитное сопротивление зазоров;

R_м1, R_мІ - магнитные сопротивление участков магнитопровода;

R_d1, R_d2 - магнитное сопротивление рассеяния;

R_м0 – магнитное сопротивление основания

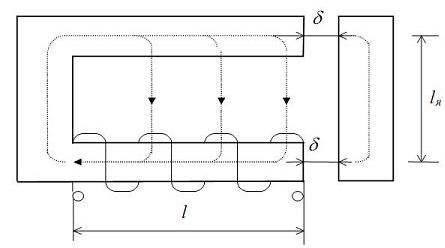
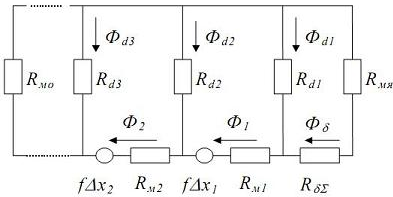
Рис. 9. К расчету магнитной системы электромагнита методом участков

Зададимся в первом приближении значением МДС:

F'=1,25 (U_мδ+U_мя), где

U_мδ - магнитное напряжение в зазоре;

U_мя - магнитное напряжение в якоре;

Найдём МДС по формуле:

F= U_мδ+ U_мя+ U_м0+ΣU_мi

Расчёт должен проводиться до тех пор, пока расхождение междуF и F' не станет меньше допустимого.

На начальном этапе расчёта по известному магнитному потоку в зазоре определяется магнитная индукция в зазоре:

B_я= Φ_δ/S_я, где

Sя – площадь сечения якоря.

Затем по кривой намагничивания выбранного материала магнитопровода находится значение H_я, а по нему магнитное напряжение в якоре:

U_мя=H_яl_я, где l_я – длина якоря.

Магнитное напряжение в зазоре:

U_мя= Φ_δR_δΣ

Поток рассеяния на первом участке:

Φ_d1= (U_мδ+ U_мя)/R_d1

Поток в сердечнике на первом участке:

Φ₁= Φ_d1+ Φ_δ

Магнитная индукция на первом участке:

B₁= Φ₁/S, где S – площадь сечения сердечника.

По кривой намагничивания находится напряжённость магнитного поля для первого участка H₁, а по нему магнитное напряжение на первом участке:

U_м1=H₁∆x₁, где

∆x₁ – длина 1-ого участка.

Поток рассеяния на втором участке:

Φ_d2= (U_мδ+ U_мя+ U_м1 – ∆x₁)/R_d2, гдеf=F'/l=1,25 (U_мδ+U_мя)/l

И так далее для каждого участка.

Расчет производится для магнитопровода, выполненного из стали 20880.

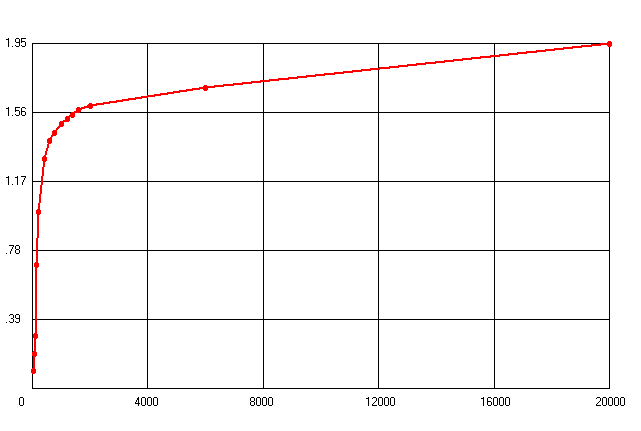
Рис. 10. Кривая намагничивания стали 20880

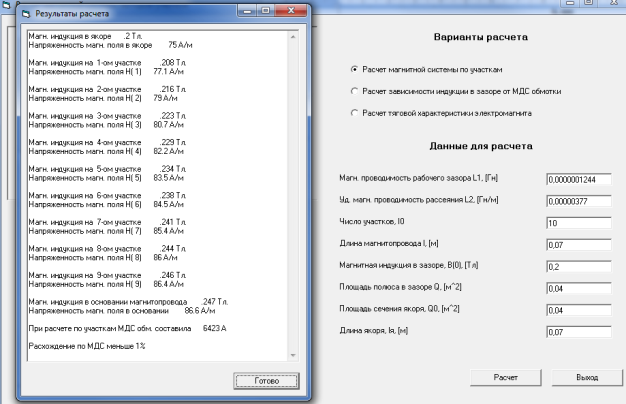
Рис. 11. Окно программы «Магнит» с исходными данными и результаты расчета

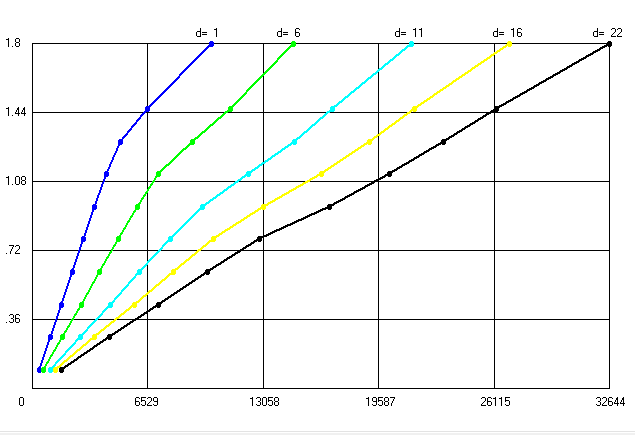
Рис. 12. Зависимость индукции в зазоре от МДС обмотки

Для полученной МДС 6423 А, используя кривые зависимости магнитной индукции от МДС для различных значений воздушного зазора (рис. 12) найдем значения магнитной индукции, а по ним при помощи формулы Максвелла ( ) значения электромагнитной силы. Результаты представлены в табл. 2

Табл. 2. Зависимость силы и индукции от величины зазора

зазор б, мм	B, Тл	F, Н
22	0,4	124,9968
16	0,5	156,2981
11	0,67	259,4756
6	1,02	601,3777
1	1,45	1215,299

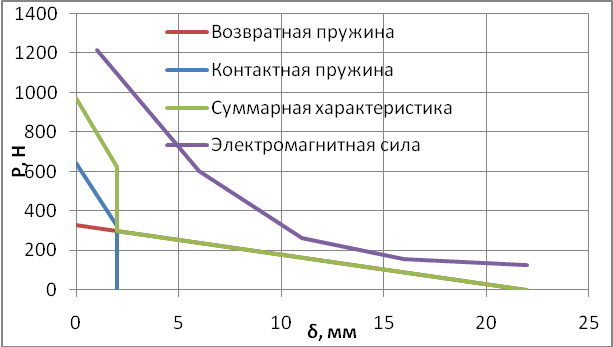
Рис. 13. Согласование характеристик пружин и электромагнита

Для всех значений зазора характеристика электромагнитной силы лежит выше суммарной характеристики противодействующих усилий. На основание этого можно сделать заключение о работоспособности спроектированного электромагнита.

Вывод

Размеры дугогасительного устройства аналога получились незначительно больше, чем размеры спроектированного устройства. Это можно объяснить тем, что при проектировании была принята идеальная модель. Реальные устройства проектируются с учетом опыта эксплуатации, результатов испытаний опытных образцов. Поэтому полученные расхождения можно считать приемлемыми.

Список литературы

1. И.С. Таев Расчет электромагнитных коммутационных реле и контакторов // Московский энергетический институт, 1997 г.

2. А.В. Савельев Проектирование электромеханических аппаратов автоматики с применением ЭВМ // Московский энергетический институт, 1998 г.

3. Е.Г. Акимов Проектирование дугогасительных устройств контакторов // Московский энергетический институт, 1982 г.

4. Ю.К. Розанов Электрические и электронные аппараты // Информэлектро, 2001 г.

Размещено на Allbest.ru