1МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

МЕДИКО-СТОМАТОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА

Медицинской и биологической физики

В.С. Воеводский А.А. Синицын В.М.Говорун

Вопросы и задачи

к экзамену по медицинской и биологической

физике для студентов стоматологического и лечебного факультетов

Часть I

3-е издание переработанное и дополненное

Москва 2008

ББК 22.3 я 73

С88

УДК 53 (075.8)

Рецензенты:

Н.Н.Фирсов - профессор кафедры ЭТФ РГМУ доктор мед. наук.

О.Ф.Беляев - профессор кафедры общей физики МГТА доктор физ. - мат. наук

Краткая аннотация

Представленные вопросы и задачи составляют основу коллоквиумов и экзаменационных билетов по курсу медицинской и биологической физики. Они охватывают три раздела курса, читаемого студентам стоматологам в первом семестре.

1.Биомеханика………………………………….

2.Гемодинамика и биореология……………...

3.Биоакустика…………………………………

4.Эталоны ответов…………………………….

Разделы начинается с примерно 20 теоретических вопросов, проработка которых необходима для решения последующих задач.

В каждом разделе задачи расположены по мере возрастания их сложности. При этом рядом расположенные задачи могут быть однотипными. Это дает возможность преподавателю, разобрав одну из них на занятиях, остальные, однотипные, задать на дом.

Ответы на все теоретические вопросы даются в лекциях, которыми в первую очередь рекомендуем пользоваться при подготовке к экзамену.

О МГМСУ, 2008-01-16

© Кафедра медицинской и биологической физики МГМСУ

© Воеводский B.C. Синицын А. А., Говорун В.М. 20008

Биомеханика

1.Дайте определения: а) относительной продольной деформации, б) относительной поперечной деформации. Приведите соответствующие математические выражения, раскройте физический смысл, входящих в них величин. Укажите единицы измерений.

2.Дайте определения: а) нормального механического напряжения, б) касательного (тангенциального) напряжения. Приведите соответствующие математические выражения, раскройте физический смысл, входящих в них величин. Укажите единицы измерений.

3.Дайте определения: а) закона упругой деформации сжатия-растяжения, б) закона упругой деформации сдвига. Приведите соответствующие математические выражения, раскройте физический смысл, входящих в них величин.

4.Дайте определение модуля упругости Е материала. Раскройте его физический смысл, укажите единицы измерения.

5.Перечислите основные виды деформаций. К каким простейшим видам их можно свести.

6.В чем отличие упругой деформации от пластической?

7.В чем особенность высокоэластической деформации? Каким телам она присуща?

8.Дайте определение момента силы, приведите соответствующие математические выражения, раскройте физический смысл, входящих в них величин, укажите единицы измерения.

9.Запишите основное условие равновесия тела, имеющего ось вращения.

10. Дайте определение коэффициента Пуассона. Приведите соответствующее

математическое выражение, раскройте физический смысл, входящих в него величин.

Укажите единицы измерений.

11.Дайте определение прочности материала. Запишите основное условие прочности.

12. В чем причина различия между технической и теоретической прочностями? Какая из них

больше и почему?

13.Перечислите основные виды разрушения материалов. Чем они отличаются?

14.Сформулируйте с "энергетической точки зрения" условие прорастания микротрещин.

Пояснения сделайте с помощью соответствующего графика.

15.Какие основные механические характеристики материалов можно определить из диаграммы

растяжения?

16. Дайте определение понятия твердости материала. Перечислите основные методы ее определения, приведите соответствующие математические выражения, раскройте физический смысл, входящих в них величин. Укажите единицы измерений.

17.Как связаны между собой основные механические характеристики материала: модуль Юнга, модуль сдвига и коэффициент Пуассона. Приведите соответствующее математическое выражение, раскройте физический смысл, входящих в него величин.

18.Что называется долговечностью материала, в чем она измеряется? Как зависит долговечность материала от приложенного механического напряжения? Приведите соответствующее математическое выражение, раскройте физический смысл, входящих в него величин.

19.Как зависит долговечность материала от температуры? Приведите соответствующее

математическое выражение, раскройте физический смысл, входящих в него величин.

20. Каков физический смысл понятия " температура хрупкости Т_хр "

21. Образец «ортосила – М» - материала для силиконовых базисных подкладок начальной длины 20 мм подвергается растяжению до относительной деформации равной 1,5. Определите получившуюся при этом длину образца.

22.Образец «ортосила – М» - материала для силиконовых базисных подкладок начальной длины 20 мм подвергается растяжению до длины 40 мм. Определите величину относительной деформации образца.

23.Образец «ортосила – М» - материала для силиконовых базисных подкладок подвергается растяжению до относительной деформации равной 2, получившаяся при этом длина образца равна 50мм. Определить начальную длину образца.

24.Каково должно быть напряжение при сжатии дентина зуба до относительной деформации 2% , если считать дентин зуба упругим материалом с модулем Юнга равным 25000 МПа?

25.Какова должна быть величина относительной деформации при сжатии дентина зуба под напряжением 4400 МПа, если считать дентин зуба упругим материалом с модулем Юнга равным 25000 МПа?

26.Каков модуль Юнга дентина зуба, если под напряжением 250 МПа, относительная величина деформации составила 2 %

27.Для изготовления проволочных элементов в ортопедической стоматологии используют

проволоку из нержавеющей стали. Отрезок проволоки длиной l = 200 мм обладает жесткостью k = 10 МН/м. определите жесткость отрезка проволоки в 1,5 раза большего, чем первый поперечного сечения, длиной 75 мм.

28. Для изготовления проволочных элементов в ортопедической стоматологии используют

проволоку из нержавеющей стали. Отрезок проволоки длиной l = 80мм обладает жесткостью k = 5 МН/м. Определите жесткость отрезка проволоки в 1,5 раза меньшего поперечного сечения длиной 85 мм.

29.Для изготовления проволочных элементов в ортопедической стоматологии используют проволоку из нержавеющей стали. Отрезок проволоки длиной l = 200 мм обладает жесткостью k = 8 МН/м. определите жесткость отрезка проволоки длиной 50мм таково же поперечного сечения.

30.Для изготовления проволочных элементов в ортопедической стоматологии используют проволоку из нержавеющей стали. Отрезок проволоки длиной l = 100 мм обладает жесткостью k = 10 МН/м. Определите жесткость отрезка проволоки длиной 300мм таково же поперечного сечения.

31.Для изготовления проволочных элементов в ортопедической стоматологии используют проволоку из нержавеющей стали. Отрезок проволоки длиной l = 200 мм обладает жесткостью k = 10 МН/м. определите жесткость отрезка проволоки в 2 раза большего поперечного сечения и 1,5 раза большей длины.

32.Какова будет жесткость двух параллельно соединенных отрезков проволоки из сплава, применяемого для изготовления кламмеров зубных протезов? Оба отрезка проволоки одинаковой длины, но различного поперечного сечения. Поперечное сечение первого отрезка в два раза больше, чем второго. Жесткость первого из отрезков K₁ = 5 МН/м.?

33.Какова будет жесткость двух последовательно соединенных отрезков проволоки из сплава, применяемого для изготовления кламмеров зубных протезов? Оба отрезка проволоки одинакового поперечного сечения, но различной длины. Длина первого отрезка в два раза больше, чем второго. Жесткость первого отрезка K₁ = 10 МН/м.?

34.Докажите, что максимальное значение коэффициент Пуассона равно 0,5

35.Покажите, что для несжимаемых материалов коэффициент Пуассона равен 0,5

36. Цилиндрический образец с начальной длиной 15 мм, изготовленный из сплава золота

подвергался испытаниям на растяжение. При этом его длина увеличилась до 16,8 мм,

а диаметр уменьшился с 7 мм до 6,8 мм. Определите коэффициент Пуассона сплава.

37.Под действием силы образец в продольном направлении удлинился в 2 раза, а в поперечном направлении деформировался в 1,6 раза. Найти коэффициент Пуассона для этого материала.

38.Во сколько раз удлинился образец в продольном направлении, если в поперечном направлении он деформировался в 1,3 раза. Коэффициент Пуассона равен 0,3.

39.Во сколько раз деформировался образец в поперечном направлении, если в продольном направлении он удлинился в 1,8 раза? Коэффициент Пуассона равен 0,32.

40.Под воздействием механического напряжения равного 150 МПа, образец из эластомера

удлинился в три раза. Чему равен модуль сдвига для этого материала?

41.Во сколько раз удлинился образец из эластомера при воздействии механического напряжения

200 МПа, если модуль сдвига для этого материала равен 40 МПа.

42.Определите модуль сдвига стали, если модуль Юнга для нее равен 300 ГПа, а коэффициент

Пуассона μ = 0,3.

43.Определите модуль упругости Е стали, если модуль сдвига для нее равен G = 80 ГПа, а

коэффициент Пуассона μ = 0,33.

44.На рисунке 1схематично представлен мостовидный протез с двумя двусторонними опорами на

естественные зубы A и B. Сосредоточенная сила F равная 800 Н приложена в точке C.

Определите силу реакции опорного зуба А если a = 3 см, а b = 2 см

Рис.1

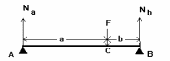
45.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на

естественные зубы A и B. Сосредоточенная сила F равная 600 Н приложена в точке C.

Определите силу реакции опорного зуба В если a = 4 см, а b = 2 см

46.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на

естественные зубы A и B. Сосредоточенная сила F равная 900 Н приложена в точке C.

Определите поперечную силу Q в сечении с координатой x = 3 см, отсчитанной от точки A,

если a = 4 см, а b = 2 см

47.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F равная 900 Н приложена в точке C. Определите поперечную силу Q в сечении с координатой x = 5 см, отсчитанной от точки A, если a = 4 см, а b = 2 см

48.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F равная 630 Н приложена в точке C. Определите изгибающий момент M(x) в сечении с координатой x = 6 см, отсчитанной от точки A, если a = 4 см, а b = 3 см.

49.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F равная 980 Н приложена в точке C. Определите изгибающий момент M(x) в сечении с координатой x = 3 см, отсчитанной от точки A, если a = 4 см, а b = 3 см.

50.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F равная 900 Н приложена в точке C. Определите расстояние от опорного зуба А, на котором изгибающий момент принимает максимальное значение, если a = 4 см, а b = 3 см.

51.На рис.1 схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F, равная 980 Н, приложена в точке C. Определите расстояния от опорного зуба А, на которых изгибающий момент принимает значение М = 9Н^. м, если, а = 3 см, а b = 4 см.

52.На рисунке 2 даны зависимости пределов хрупкой прочности и текучести от температуры

Рис. 2

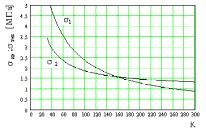
Какое разрушение хрупкое или пластическое будет у образца при температуре 200 K?

53.На рис.2 даны зависимости пределов хрупкой прочности и текучести от температуры

Какое разрушение хрупкое или пластическое будет у образца при температуре 100 K?

54.На рис.2 даны зависимости пределов хрупкой прочности и текучести от температуры для

некоторого материала.

Определить предел текучести при температуре 260 К

55.На рис. 2 даны зависимости пределов хрупкой прочности и текучести от температур

Определить предел хрупкой прочности при температуре 80 К

56.На рис.2 даны зависимости пределов хрупкой прочности и текучести от температуры

Определить предел хрупкой прочности при температуре 40 К

57.На рис.2 даны зависимости пределов хрупкой прочности и текучести от температуры

Найти максимальную температуру, при которой образец хрупко разрушается

58.На рис.2 даны зависимости пределов хрупкой прочности и текучести от температуры

Найти минимальную температуру, при которой образец пластично разрушается

59. На рис.2 представлены зависимости предела хрупкой прочности и предела текучести

от абсолютной температуры.

Какое разрушение хрупкое или пластическое будет у образца сплава при температуре 250 K?

60. На рисунке 3 представлены графики зависимости потенциальной энергии W [Дж]

образца фосфорокерамического материала, применяемого для изготовления искусственных

зубов, от длины трещины при двух напряжениях.

Рис.3

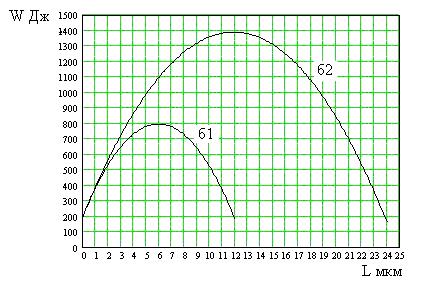
Определите минимальную длину трещины, начиная с которой она будет расти.

Образец находится под действием большего напряжения.

61. На рис.3 представлены графики зависимости потенциальной энергии W [Дж]

образца фосфорокерамического материала, применяемого для изготовления искусственных

зубов, от длины трещины при двух напряжениях.

Определите минимальную длину трещины, начиная с которой она будет расти.

Образец находится под действием меньшего напряжения.

62. На рис.3 представлены графики зависимости потенциальной энергии W [Дж] образца

фосфорокерамического материала, применяемого для изготовления искусственных зубов,

от длины трещины при двух напряжениях.

Определите максимальную длину трещины, начиная с которой она не будет расти.

Образец находится под действием меньшего напряжения.

63. На рис.3 представлены графики зависимости потенциальной энергии W [Дж]

образца фосфорокерамического материала, применяемого для изготовления

искусственных зубов, от длины трещины при двух напряжениях

Напряжение σ₁ равно 0,6 МПа. Определить напряжение σ ₂

64. На рис.3 представлены графики зависимости потенциальной энергии W [Дж]

образца фосфорокерамического материала, применяемого для изготовления искусственных зубов, от длины трещины при двух напряжениях

Напряжение σ₂ равно 0,5 МПа. Найти напряжение σ₁.

65. На рисунке 4 представлены зависимости критического напряжения σ от длины

микротрещины L для материала, находящегося в средах с различными коэффициентами

поверхностного натяжения α. Найти отношение коэффициентов α₁ к α₂?

Рис.4

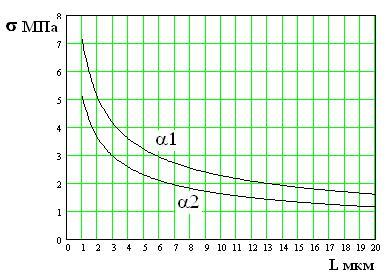
66. Рис.4. Во сколько раз изменится критический размер микротрещины, если растягивающее

напряжение увеличится в два раза?

67. Рис. 4. Во сколько раз изменится критическое напряжение, если размер микротрещины уменьшится

в 9 раз?

68. Рис.4. Радиус в вершине микротрещины увеличился в 4 раза. Во сколько раз изменится при этом

локальное напряжение в вершине микротрещины?

69.На рисунке 5 представлена зависимость логарифма долговечности материала от напряжения

при различных температурах: 350 К, 300 К, 250 К .

Рис.5

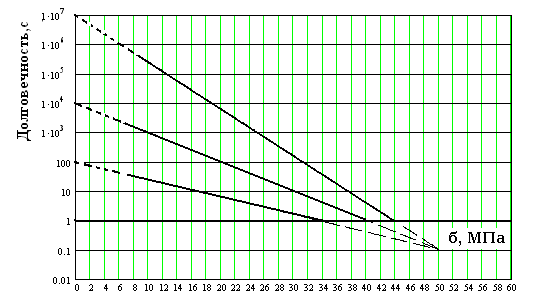
Определить долговечность материала при температуре 250 К и механическом напряжении

38 МПа.

70.На рисунке 5 представлена зависимость логарифма долговечности материала от напряжения

при различных температурах: 350 К, 300 К, 250 К

Определить долговечность материала при 350 К и механическом напряжении 34 МПа.

71.На рисунке 5 представлена зависимость логарифма долговечности материала от напряжения

при различных температурах: 350 К, 300 К, 250 К

Определить долговечность материала при температуре 300 К и напряжении 20 МПа.

72.На рис. 6 представлены температурные зависимости долговечности образцов

материала для базисов протезов при различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Рис. 6

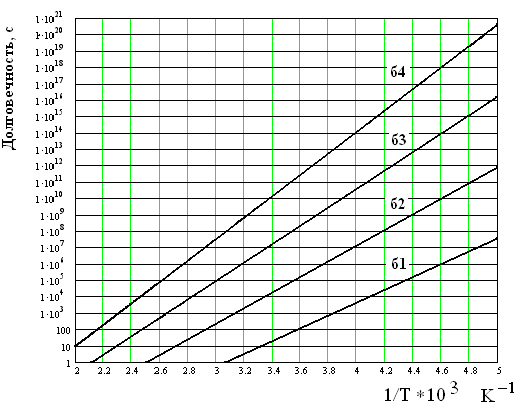
Определить долговечность образца, находящегося под напряжением 2 МПа, при температуре

60 ⁰ С.

73. На рис. 6 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 1 МПа при

температуре 227 ⁰ С.

74.На рис. 6 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 2 МПа при температуре -65 ⁰ С.

75.На рис. 6 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 3 МПа при температуре -35 ⁰ С.

76.На рис. 6 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 5 МПа при температуре 5 ⁰ С.

77.На рис. 6 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 1 МПа при температуре -23 ⁰ С.

78. На рис. 7 представлены температурные зависимости логарифма долговечности образцов при

различных напряжениях: 5 МПа, 3 МПа, 2 МПа, 1 МПа

Определить долговечность образца, находящегося под напряжением 5 МПа при температуре -55 ⁰ С.

Рис.7

Определить долговечность образца, находящегося под напряжением 2 МПа, при температуре

60 ⁰ С.

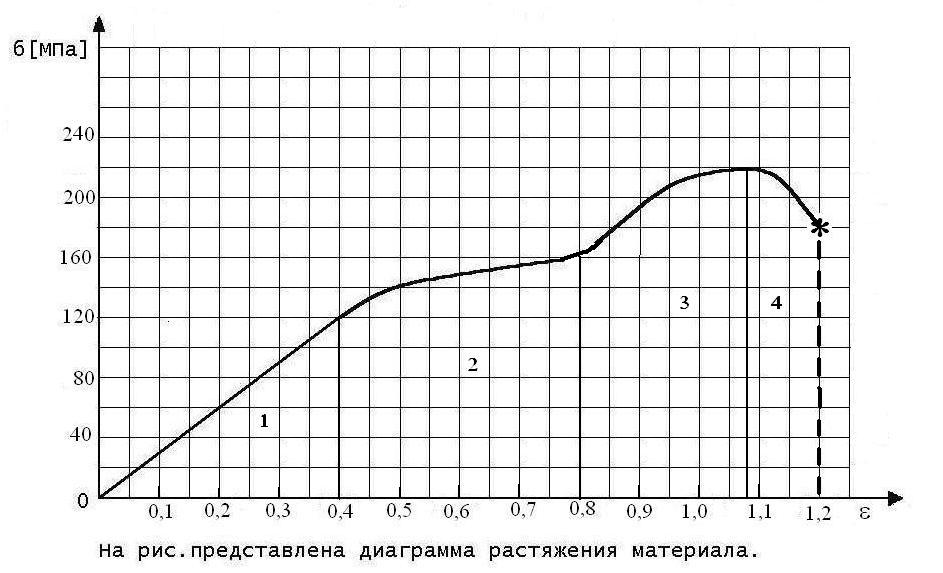
79. Рис.7 Определить предел прочности материала

80. Рис.7 На каком участке выполняется закон упругой деформации Гука.

81. Рис.7 Определить модуль упругости материала E.

82. Рис.7 Во сколько раз модуль упругости E материала больше предела прочности σ _пр.

83. Рис.7 Во сколько раз растянулся образец при разрыве.

84. Рис.7 Конечная длина образца при разрыве 66 см. Найти его начальную длину.

85. Рис.7 Начальная длина образца 40 см,. При какой длине он разорвался.

86. Рис.7 Модуль сдвига материала 115 МПа. Чему равен коэффициент Пуассона материала.

87. Рис.7 Коэффициент Пуассона μ равен 0,35. Чему равен модуль сдвига у этого материала.

88. Рис.7 Определить максимальную объемную плотность энергии упругой деформации.

89. Рис.7 Во сколько раз предел прочности больше предела упругости.

90. Рис.7 Найти относительную деформацию предела упругости.

91. Рис.7 Во сколько раз относительная деформация при разрыве больше относительной деформации предела упругости.

92. Рис.7 Начальная длина образца 10см. Площадь сечения 2см ². Определить максимальную работу

упругой деформации.

93. Рис.7 Во сколько раз растянулся образец при максимальной упругой деформации.

94. Рис. 7 Коэффициент Пуассона μ равен 0,35. Найти истинное механическое напряжение в начале пластической деформации.

Гемодинамика

1.Дайте определение понятия "идеальная жидкость". Приведите основные уравнения,

описывающие течение идеальной жидкости.

2.Чем отличается реальная жидкость от идеальной?

3.Запишите условие стационарного течения (неразрывности струи). Объясните физический смысл этого условия и входящих в него величин.

4.Запишите уравнение Бернулли. Объясните физический смысл, входящих в него величин.

5.Запишите уравнение Ньютона для вязкого течения жидкости. Поясните физический смысл, входящих в него величин.

6.От чего зависит коэффициент вязкости  для ньютоновских и неньютоновских жидкостей.

7.Нарисуйте график зависимости касательного напряжения τ от скорости сдвига для ньютоновской и неньютоновской жидкостей. Как на графике проявляется коэффициент вязкости для ньютоновской жидкости?

8.Запишите выражение для скорости течения различных слоев жидкости в цилиндрических сосудах. Поясните физический смысл, входящих в него величин.

9.Запишите закон Пуазейля. Поясните физический смысл, входящих в него величин и единицы их измерений.

10.Запишите выражение для гидравлического сопротивления жидкости. Поясните физический смысл, входящих в него величин и единицы их измерений.

11.Чем отличается ламинарное течение жидкости от турбулентного? Запишите критерий Рейнольдса. Поясните физический смысл, входящих в него величин и единицы их измерений.

12.Нарисуйте и объясните график зависимости касательного напряжения τ от скорости

сдвига для плазмы и цельной крови.

13.Нарисуйте и объясните график зависимости коэффициента вязкости η от скорости сдвига для плазмы и цельной крови.

14.Опишите физические процессы, лежащие в основе измерения артериального давления по Короткову.

15.Запишите уравнение Кессона. Поясните физический смысл, входящих в него величин и единицы их измерений. Раскройте понятие "кессоновской вязкости".

16.Запишите зависимость вязкости крови η от показателя гематокрита. Поясните физический смысл, входящих в него величин и единицы их измерений.

17.Во сколько раз изменится объемная скорость кровотока при переходе от участка сосудистого русла с общей площадью поперечного сечения S(1) = 150 мм ² к участку сосудистого русла с общей площадью поперечного сечения S(2) = 900 мм ²

18.Определите время прохождения крови через капилляр длины l = 800 мкм, средняя линейная скорость течения крови в аорте 15 см/с, а площадь поперечного сечения капиллярного русла в 700 раз превосходит площадь поперечного сечения аорты.

19.Определите длину капилляра, если время прохождения крови через него равно 5 с. средняя линейная скорость течения крови в аорте 20 см/с, а площадь поперечного сечения капиллярного русла в 800 раз превосходит площадь поперечного сечения аорты.

20.Время прохождения крови через капилляр длины l = 800 мкм, равно 4 с. Определить среднюю линейную скорость течения крови в аорте, если площадь поперечного сечения капиллярного русла в 600 раз превосходит площадь поперечного сечения аорты

21.Какова будет средняя линейная скорость кровотока в участке сосудистого русла с общей

площадью поперечного сечения 500 см ², если в аорте диаметром 15 мм скорость крови составляет 20 см/с?

22.Какова будет средняя линейная скорость кровотока в аорте диаметром 20 мм, если на участке сосудистого русла с общей площадью поперечного сечения 500 см ², она равна

0,5 мм/с?

23.Чему равна общая площадь участка сосудистого русла, если средняя линейная скорость кровотока в нем равна 0,4 мм/с, а в аорте диаметром 25 мм скорость крови составляет 25 см/с?

24.Во сколько раз изменится средняя линейная скорость кровотока при переходе от участка сосудистого русла

с общей площадью поперечного сечения S(1) = 160 мм ² к участку сосудистого русла с общей площадью

поперечного сечения S(2) = 900 мм ²

25.Конструкция бифуркационного протеза такова, что диаметр дочерней ветви равен 60% от диаметра

основного ствола протеза. Определите среднюю линейную скорость крови в дочерних ветвях при включении

магистрального кровотока, если средняя скорость в основном стволе составляла 30 см/с.

26.Конструкция бифуркационного протеза такова, что диаметр дочерней ветви равен 65% от диаметра основного ствола протеза. Определите среднюю линейную скорость крови в основном стволе при включении магистрального кровотока, если средняя скорость в дочерних ветвях составляла 60 см/с.

27.Идеальная жидкость течет по горизонтальному сосуду переменного сечения. Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 2,5м/с радиус R₁ = 4 см радиус R₂ = 2 см., полное давление Р = 10 ⁵ Па. Найти статическое давление

Р ₁ в первом сечении S₁ .

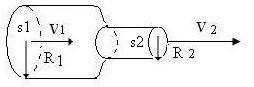
28.Идеальная жидкость течет по горизонтальному сосуду переменного сечения. Плотность жидкости ρ =10 ³кг/м³ скорость в первом сечении S₁ V₁ = 0,8 м/с, радиус R₁ = 3 см радиус R₂ = 2 см., Найти динамическое давление во втором сечении S₂ .

29.Идеальная жидкость течет по горизонтальному сосуду переменного сечения. Плотность жидкости ρ =1000кг/м³ скорость в первом S(1) сечении V₁ = 1м/с, радиус R₁ = 4 см радиус R₂ = 3 см., полное давление Р =10⁵ Па. Найти статическое давление Р ₂ в сечении S₂ .

30.Идеальная жидкость течет по горизонтальному сосуду переменного сечения. Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 3м/с, радиус R₁ =5 см радиус R₂ = 3 см., полное давление Р =10 ⁵ Па. Найти статическое давление Р ₁ в первом сечении S₁

31. Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ =0,5м/с, радиус R₁ =4 см радиус R₂ = 3 см., Найти динамическое давление во втором сечении S₂ .

32.Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 0,7м/с, радиус R₁ = 4 см радиус R₂ = 2 см., Найти динамическое давление во втором сечении S₂ .

33. Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ =1,5м/с, радиус R₁ = 5 см радиус R₂ = 2 см., Найти динамическое давление во втором сечении S₂ .

34.Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 0,5м/с, радиус R₁ = 4 см радиус R₂ = 2 см., статическое давление в первом сечении Р₁ = 10⁴ Па. Найти статическое давление Р ₂ в сечении S₂

35.Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 3м/, радиус R₁ =4 см радиус R₂ = 3 см., полное давление Р =10 ⁵ Па. Найти статическое давление Р ₁ в первом сечении S₁ .

36.Идеальная жидкость течет по горизонтальному сосуду переменного сечения

Плотность жидкости ρ =1000кг/м³ скорость в первом сечении S₁ V₁ = 1м/с, радиус R₁ = 4 см радиус R₂ = 3 см., статическое давление в первом сечении Р₁ = 10⁴ Па. Найти статическое давление Р ₂ в сечении S₂ .

37.В высоком вертикально стоящем цилиндрическом сосуде, заполненном ньютоновской жидкостью, падает с постоянной скоростью 0,3 см/с стальной шарик диаметром 2 мм. С какой постоянной скоростью будет падать в этом сосуде стальной шарик диаметром 1 мм?

38.В опыте с капиллярным вискозиметром вязкость эталонной жидкости равнялась 1,5 мПас, плотность ее составляла 800 кг/м³ . Вязкость исследуемой жидкости оказалась равной

4 мПас, а плотность составила 1200 кг/м³. Время истечения через капилляр 5 мл исследуемой жидкости равно 10 с. Определить время истечения через капилляр 3 мл эталонной жидкости.

39.В опыте с капиллярным вискозиметром вязкость эталонной жидкости равнялась 2 мПас, плотность ее составляла 800 кг/м³ . Вязкость исследуемой жидкости оказалась равной

3 мПас, а плотность составила 1200 кг/м³. Время истечения через капилляр 4 мл исследуемой жидкости равно 10 с. Какой объем эталонной жидкости вытечет через 8 с.

40.Определите скорость, с которой должен равномерно двигаться эритроцит при наблюдаемой реакции СОЭ. Считать эритроцит шариком с диаметром 8 мкм. Плотность эритроцита равна 1085 кг/м³, плотность плазмы крови составляет 1035 кг/м³ .

Вязкость плазмы крови равна 1,4 мПас.

41.Кровеносный сосуд с радиусом просвета 2 мм разделился на две ветви с радиусами по

1,5 мм. Во сколько раз при этом изменилось гидравлическое сопротивление, приходящееся на единицу длины сосудистого русла?

42.Найти радиус кровеносного сосуда, который разделился на две ветви с радиусами по 1,5мм. При этом гидравлическое сопротивление, приходящееся на единицу длины сосудистого русла, увеличилось в три раза.

43. Кровеносный сосуд с радиусом просвета 5 мм разделился на две ветви одинаковых радиусов. При этом гидравлическое сопротивление, приходящееся на единицу длины сосудистого русла, увеличилось в 2 раза. Определить радиусы ветвей сосудов.

44.При уменьшении радиуса просвета кровеносного сосуда в 2 раза и увеличении вязкости

крови в 1,5 раза во сколько раз изменится его гидравлическое сопротивление?

45. Во сколько раз изменится гидравлическое сопротивление кровеносного сосуда, если его

радиус уменьшится на 40 %?

46.Гидравлическое сопротивление кровеносного сосуда, уменьшилось на 50 %.

Во сколько раз изменился его радиус?

47.Для аллопластики бифуркации брюшной аорты необходимо изготовить протез так, чтобы кровь не травмировалась вследствие действия гидродинамических факторов, возникающих при движении ее через протез. Диаметр основного ствола протеза должен быть равен 15 мм. Определите значение диаметра дочерней ветви протеза.

48.Для аллопластики бифуркации брюшной аорты необходимо изготовить протез так, чтобы кровь не травмировалась вследствие действия гидродинамических факторов, возникающих при движении ее через протез. Диаметр дочерней ветви протеза ранен 9 мм. Определить диаметр основного ствола протеза?

49. Рис.1 Максимальная скорость движения жидкости на первом участке радиуса R=1,5 см. равна

V= 50 см/с. Определить вязкость жидкости

Рис. 1

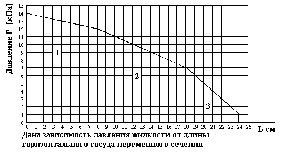
50. Рис. 1 Гидравлическое сопротивление на первом участке Х = 50_*10 ⁵ Па^. с/м³

Найти объемную скорость течения на этом участке.

51. Рис.1 Объемная скорость Q равна 150 мл/с. Найти гидравлическое сопротивление на участке 3

52. Рис.1 Объемная скорость Q равна 100 мл/с. Найти гидравлическое сопротивление на участке 2

53. Рис.1 Найти отношение гидравлических сопротивлений на участках 2 к 1.

54. Рис.1 Объемная скорость Q равна 200 мл/с. Найти гидравлическое сопротивление на участке1

55. Рис.1 Вязкость жидкости равна 4 Па^. с. Радиус сосуда на 2 участке равен 1,5 см.

Найти скорость движения жидкости на расстоянии 1 см от оси сосуда.

56. Рис.1 Вязкость жидкости равна 4 Па^.с. Радиус сосуда на 1 участке равен 2 см.

Найти скорость движения жидкости на расстоянии 1 см от оси сосуда.

57. Рис.1 Найти отношение гидравлических сопротивлений на участках 2 к 3.

58. Рис.1 Найти отношение гидравлических сопротивлений на участках 3 к 1.

59. Рис.1 Максимальная скорость движения жидкости на третьем участке радиуса R=0,5 см.

равна 20 см/с. Определить коэффициент вязкости жидкости.

60. Рис.1 Объемная скорость Q равна 100 мл/с. На участке 1 радиус R= 2 см.

Найти коэффициент вязкости.

61. Рис.1 Объемная скорость Q равна 150 мл/с. На третьем участке радиус R= 1см .

Найти коэффициент вязкости.

62.Периферическое сопротивление у пациента увеличилось на 10%. На сколько процентов изменился

минутный объем циркуляции, если артериальное давление увеличилось на 15 %?

63.Минутный объем циркуляции крови увеличился на 4 %. На сколько процентов изменилось периферическое сопротивление у пациента, если артериальное давление уменьшилось

на 10%?

64.Периферическое сопротивление у пациента увеличилось на 15%. На сколько процентов изменилось артериальное давление, если минутный объем циркуляции увеличился на 10 %?

65.Два соседних участка артериального русла имеют диаметры просветов d (1) = 15 мм и

d (2) = 6 мм. Определите отношение гидравлическое сопротивления, приходящегося на единицу длины второго

участка к аналогичной величине первого участка.

66.Во сколько раз изменится гидравлическое сопротивление, приходящееся на единицу длины сосудистого участка, при разветвлении крупного сосуда на N мелких при равенстве их общей площади и площади крупного сосуда S₀ = N^. s?

67.Чему равно общее гидравлическое сопротивление 5 одинаковых параллельных кровеносных сосудов с гидравлическим сопротивлением каждого равным - Х?

68.Определите отношение гидравлическое сопротивления участка, содержащего артериолы, к гидродинамическому сопротивлению участка кровеносного русла человека, содержащего капилляры. Диаметр просвета артериолы составляет 0,007 мм, длина артериолы равна 0,9 мм, общее число артериол 410 ⁸. Диаметр капилляра составляет

0,004 мм, длина - 0,2 мм, общее число капилляров в сосудистом русле человека 210 ⁹.

69.Какова должна быть разность давлений на концах горизонтально расположенной цилиндрической трубки, длина которой равна 50 см и радиус просвета 2 мм, чтобы по ней ламинарно протекала ньютоновская жидкость со скоростью на оси трубки V = 50 см/с? Коэффициент динамической вязкости равен 1,2 мПа _*с.

70.Кровеносный сосуд с радиусом просвета 15 мм разделился на две ветви с радиусами по

11 мм. Во сколько раз при этом изменилось гидродинамическое сопротивление, приходящееся на единицу длины сосудистого русла

71.Во сколько раз отличается гидравлическое сопротивление участка кровеносного сосуда радиуса 1,5 мм и длины 4 мм от гидравлическое сопротивления участка кровеносного сосуда с радиусом 0,5 мм и длиной 1 мм?

72.При перфузии кровеносной системы кошки кровью было получено значение гидродинамического сопротивления Х(1), затем кровь заменили раствором реополиглюкина с коэффициентом вязкости 3 мПас и получили значение гидравлическое сопротивления Х(2) на 20 % меньше, чем Х(1). Найдите вязкость крови кошки, если перфузионное давление поддерживалось постоянным.

73.Для аллопластики бифуркации брюшной аорты необходимо изготовить протез так, чтобы кровь не

травмировалась вследствие действия гидродинамических факторов, возникающих при движении ее через

протез. Определите отношение гидравлического сопротивления, приходящееся на единицу длины участка

протеза после разветвления, к значению аналогичной величины основного ствола протеза.

74.Определите высоту над постелью больного, на которой висела капельница. Если в вену предплечья вводился раствор лекарственных веществ плотностью ρ = 1020 кг/м³ и вязкостью

η =1,5 мПа_*с, давление в вене составлялоP = 70 мм водного столба. Игла, введенная в вену, имела диаметр просвета равный 0,4 мм, длину 60 мм. Через капельницу в венозное русло больного поступило 200 мл раствора за 120 минут. Считать режим течения в игле ламинарным.

75.По магистральному кровеносному сосуду ламинарно течет кровь под действием разности давлений на концах сосуда ΔP = 5 мм.рт.ст., длина рассматриваемого участка сосуда равна

5 см. Определите напряжение сдвига τ на расстоянии 6 мм от оси сосуда. Кровь считать ньютоновской жидкостью.

76.По кровеносному капилляру с радиусом просвета R = 2,5 мкм протекает в ламинарном режиме кровь со средней линейной скоростью 1,5 мм/с. Определите значение скорости сдвига у стенки капилляра.

77.Сколько тепла выделится в одном 1см ³ за 1c при ламинарном течении ньютоновской жидкости, если при

напряжении сдвига 0,8 Па, скорость сдвига 10 с ^{- 1}?

78.При увеличении скорости кровотока в 1,4 раза, увеличении радиуса сосуда в 1,5 раза и

уменьшении вязкости крови в 2 раз, во сколько раз изменилось число Рейнольдса?

79.Когда человек делает вдох через нос, сквозь ноздри (диаметр 1 см) воздух проходит со средней скоростью V = 450 см/с. Воздух имеет коэффициент динамической вязкости

17 мкПа _*с, плотность - 1,3 кг/м³ . Определите значение числа Рейнольдса.

80.Когда человек делает вдох через нос, сквозь ноздри (диаметр 0,8 см) воздух проходит со средней скоростью V = 260 см/с. Воздух имеет коэффициент динамической вязкости

17 мкПас, плотность - 1,3 кг/м³. Каков при этом режим течения воздуха и почему?

81.В одной из магистральных артерий человека максимальное значение числа Рейнольдса 1300 Диаметр просвета сосуда равен 15 мм, плотность крови равна 1050 кг/м³, коэффициент динамической вязкости крови принять равным 4 мПас. Определить максимальную линейную скорость кровотока в артерии.

«82.Кажущаяся вязкость образца крови составила 0,1 Пас. Определите значение кажущейся вязкости крови при увеличении гематокрита на 25 % (при той же скорости сдвига и температуре), если считать, что состав плазмы крови не изменился. Вязкость плазмы составляет 1,5 мПас.

««83. На рис. 2 Представлена зависимость вязкости крови от показателя гематокрита.

Рис. 2

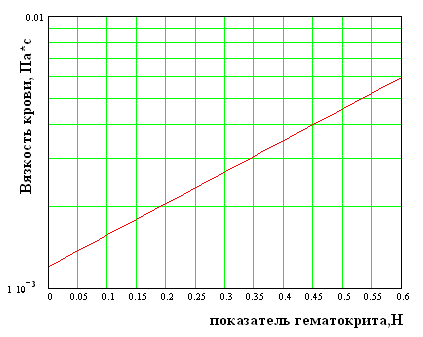
Определить по этим данным вязкость крови при показателе гематокрита Н = 0,45

«84. Рис. 2 Определить по этим данным вязкость плазмы крови.

«85.При исследовании реологических свойств крови получены данные, представленные на рис.3

Рис.3

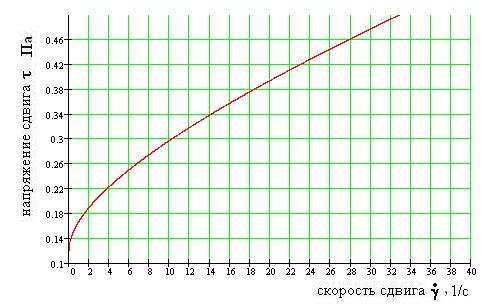
Определите по этим данным, предполагая, что для крови применима модель Кессона, отношение кажущейся вязкости при скорости сдвига = 28 ,1/с к кажущейся вязкости при скорости сдвига = 4.

«86. При исследовании реологических свойств крови получены данные, представленные на рис.3

Определите по этим данным, предполагая, что для крови применима модель Кессона,

асимптотическую вязкость крови η _∞.

«87. При исследовании реологических свойств крови получены данные, представленные на рис. 3

Определите по этим данным, предполагая, что для крови применима модель Кессона, предел текучести τ ₀ крови.

«88. Рис. 4

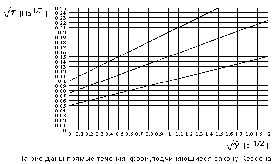
Для прямой, соответствующей асимптотической вязкости η_∞ = 10 мПа_*с, определить кажущуюся вязкость крови при скорости сдвига ^ = 1,44 ,с ^{- 1} .

«89. Рис.4 Для прямой, соответствующей асимптотической вязкости η_∞ = 2,5 мПа _*с, определить кажущуюся вязкость крови при скорости сдвига = 4 ,с ^{- 1} .

«90. Рис. 4 Для прямой, соответствующей асимптотической вязкости η_∞ = 5,6 мПа _*с, определить кажущуюся вязкость крови при скорости сдвига = 1 ,с ^-1 .

«91. Рис. 4 Для прямой, соответствующей асимптотической вязкости η_∞ = 2,5 мПа _*с, определить напряжение сдвига τ при скорости сдвига = 1,69 ,с^-1 .

«92. Рис. 4 Для прямой, соответствующей асимптотической вязкости η_∞ = 2,5 мПа_*с, определить напряжение сдвига τ при скорости сдвига = 0,09 ,с ^-1 .

«93. Рис. 4. Для прямой, соответствующей асимптотической вязкости η_∞ = 5,6 мПа_*с, определить напряжение сдвига τ при скорости сдвига ^ = 0,01 ,с^-1

«94.При исследовании реологических свойств крови получены данные, представленные на рис. 5

Определите по этим данным, предполагая, что для крови применима модель Кессона,

отношение асимптотической вязкости η_∞ к кажущейся вязкости при скорости сдвига

= 28 ,1/с.

«95. При исследовании реологических свойств крови получены данные, представленные на рис. 5

Определите по этим данным, предполагая, что для крови применима модель Кессона,

отношение асимптотической вязкости η_∞ к кажущейся вязкости при скорости сдвига

= 4 ,1/с.

«96. При исследовании реологических свойств крови получены данные, представленные на рис. 5

Определите по этим данным, предполагая, что для крови применима модель Кессона, кажущуюся вязкость крови при скоростей сдвига = 4 ,с ^-1.

«97. При исследовании реологических свойств крови получены данные, представленные на рис. 5

Определите по этим данным, предполагая, что для крови применима модель Кессона, кажущуюся вязкость крови при скорости сдвига = 14 ,1/с.

«98. При исследовании реологических свойств крови получены данные, представленные на рис. 5

Определите по этим данным, предполагая, что для крови применима модель Кессона, отношение кажущейся вязкости при скорости сдвига 4 ,1/с к кажущейся вязкости при скорости сдвига 14 ,1/с.

«99. При исследовании реологических свойств крови получены данные, представленные на рис.

Определите по этим данным, предполагая, что для крови применима модель Кессона,

отношение кажущейся вязкости при скорости сдвига - 14 ,с ^-1 к асимптотической η_∞.

100. На рис. 6 представлена зависимость кажущейся вязкости образца крови от скорости сдвига

Рис. 6

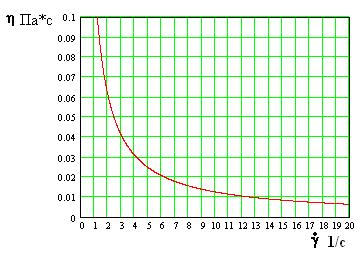
При каком напряжении сдвига получена эта кривая?

101.Каково будет среднее кольцевое напряжение σ в стенке цилиндрического кровеносного

сосуда с толщиной стенки h = 0,05см и диаметром просвета d = 1см, если внутри

просвета давление крови P(i) = 900 мм рт. ст., а давление вне сосуда равно 750 мм.рт.ст.?

( 1мм.рт.ст. = 133 Па)

102.Определите значение давления в полости левого желудочка сердца, при котором

напряжение в стенке желудочка составляет σ= 50 кПа, толщина стенки желудочка h =

10мм. Желудочек считать сферической оболочкой, диаметром 6см. Внешнее давление

принять равным атмосферному P = 750 мм рт.ст. (1мм.рт.ст. = 133 Па)

103. Рассчитайте среднюю работу и мощность сердца исходя из данных, приводимых на

лекции.

!«104. Напряжение в упругом элементе модели упруговязкого тела составляет 20 Па. Модуль

упругости упругого элемента 1 Па, коэффициент динамической вязкости

ньютоновского элемента 0,13 Пас. Определите напряжение в вязком элементе.

«105. Относительная деформация упругого элемента вязкоупругой системы 0,9. Модуль упругости

упругого элемента 2 Па, а коэффициент вязкости вязкого элемента 2 мПас. Определите

относительную деформацию ε вязкого элемента.

«106. Какую скорость деформации сдвига 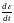вызовет в веществе, реологическое поведение

которого соответствует модели вязкопластичного тела, напряжение сдвига τ =10 мПа, если

коэффициент вязкости ньютоновского элемента η = 4 мПас, а предел текучести τ₀ = 5 мПа

«107. Материал, поведение которого описывается вязкоупругой моделью, находится под

действием постоянно приложенного напряжения σ = 120 Па за время 15 с. Определите значение

максимальной относительной деформации, если модуль упругости элемента Гука Е = 20 Па, а

коэффициент вязкости вязкого элемента 50 Пас

«108. Вязкоупругое тело испытывают на ползучесть. Коэффициент вязкости вязкого элемента

100 Пас, а модуль упругости упругого элемента 10 Па. Определите значение относительной

деформации спустя время 5 с после нагружения, если напряжение в теле поддерживалось

постоянным и равным 20 Па.

«109.Вещество, реологическое поведение которого соответствует модели упруго вязкого тела,

находится под действием постоянного напряжения σ =15 Па. Спустя t = 40 с после

внезапного приложения указанного напряжения относительная деформация ε составила 2 %.

Определите коэффициент динамической вязкости η модели.

!«110.Напряжение в вязком элементе модели упруговязкого тела σ = 6 Па. Модуль

упругости упругого элемента E = 10 Па, коэффициент динамической вязкости

ньютоновского элемента η = 0,4 Пас. Определите относительную деформацию ε упругого элемента.

«111. При испытании на релаксацию механического напряжения упруговязкое тело мгновенно

деформируют. В момент окончания деформирования напряжение 700 мПа. Определите напряжение

в теле спустя 0,5 с, если коэффициент вязкости ньютоновского элемента 70 мПас,

а модуль упругости элемента 140 мПа.

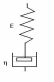
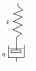« 112. В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянной деформации заданы:

Модуль упругости Е = 10 кПа ,Коэффициент вязкости η = 50 кПа_*с ,

Начальное напряжение σ₀ =10 кПа.Найти напряжение в модели через t = 8 с.

1»113. В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянной деформации заданы:

Модуль упругости Е =15 кПа, Коэффициент вязкости η = 60 кПа_*с,

Начальное напряжение σ₀ = 30 кПа. Найти время, по истечению которого напряжение станет равным σ = 7 кПа.

«114. 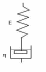В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянной деформации заданы:

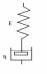М одуль упругости Е =10 кПа, Начальное напряжение σ₀ = 50 кПа,Конечное напряжение через 5 с стало равно σ =18,4 кПа. Определить коэффициент вязкости η

115. В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянной деформации заданы:

Модуль упругости Е =15 кПа, Коэффициент вязкости η = 60 кПа_*с,

Конечное напряжение через 8 с σ = 2,7 кПа

Определить начальное напряжение σ ₀

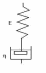
116. В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянной деформации заданы:

Коэффициент вязкости η = 100 кПа_*с, Начальное напряжение σ₀ = 30 кПа. Конечное напряжение через 6 с σ = 6,7 кПа.Определить модуль упругости Е

117.

В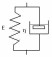 представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянном напряжении заданы:Модуль упругости Е =10 кПа Коэффициент вязкости η = 30 кПа_*с, Напряжение σ = 80 кПа.Определить относительную деформацию  через 4 с после приложения напряжения.

118 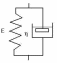В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянном напряжении заданы:

Модуль упругости Е =10 кПа. Коэффициент вязкости η = 20 кПа_*с, Напряжение σ = 80 кПа. Через какое время t относительная деформация стала равной ε = 6,2

119.

В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянном напряжении заданы:Модуль упругости Е = 20 кПа. Напряжение σ = 50 кПа

Ч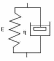 ерез 5 с после приложения напряжения относительная деформация стала равна ε = 2. Определить коэффициент вязкости

1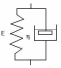 20. В представленной на рисунке простейшей механической модели биологической ткани, находящейся при постоянном напряжении заданы:

Модуль упругости Е =10 кПа. Напряжение σ = 60 кПа. Через 3 с после приложения напряжения относительная деформация стала равна ε = 1,7.

Определить коэффициент вязкости η

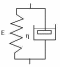« 121.В представленной на рисунке простейшей механической модели биологической ткан, находящейся при постоянном напряжении заданы:

иМодуль упругости Е =10 кПа

Коэффициент вязкости η = 40 кПа_*с

Через 3 с после приложения напряжения относительная деформация стала равна ε = 2,64

Определить приложенное напряжение σ

122. Нарисуйте график зависимости относительной деформации от времени для вязко упругого тел, находящегося при постоянном напряжении.

123. Нарисуйте график зависимости относительной деформации ε от времени для упруговязкого тела, находящегося при постоянном напряжении.

124. Нарисуйте график зависимости напряжения  от скорости сдвига для вязкопластического тела.

«125. На рис. 7 даны кривые ползучести различных материалов. Определить время релаксации 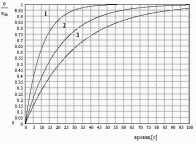первого материала

Рис. 7

«126. На рис. 7 даны кривые ползучести различных материалов. Для первого материала, модуль упругости которого равен Е = 10 МПа, определить коэффициент вязкости.

«127. На рис. 7 даны кривые ползучести различных материалов. Для второго материала, модуль упругости которого равен Е = 20 МПа, определить коэффициент вязкости.

128. На рис. 7 даны кривые ползучести различных материалов. Для третьего материала, модуль упругости которого равен Е = 20 МПа, определить коэффициент вязкости.

«129. На рис. 7 даны кривые ползучести различных материалов. Для первого материала, коэффициент вязкости которого η = 40 МПа_*с, определить модуль упругости Е.

130. На рис. 7 даны кривые ползучести различных материалов. Для второго материала, коэффициент вязкости которого η = 100 МПа_*с, определить модуль упругости Е.

«131. На рис. 7 даны кривые ползучести различных материалов. Для третьего материала, коэффициент вязкости которого η = 90 МПа_*с, определить модуль упругости Е.

«132. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Определить время релаксации для первого материала.

Рис. 8

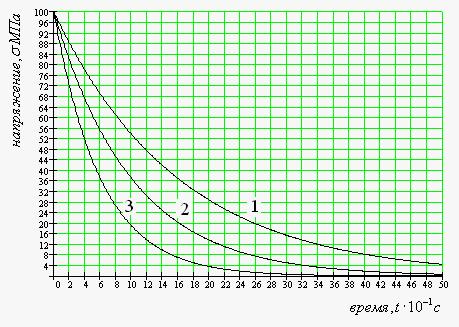
«133. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Определить время релаксации для второго материала.

«134. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Определить время релаксации для третьего материала.

«135. На рис.8 представлены кривые релаксации напряжения для трех различных материалов. Для первого материала, модуль упругости которого равен Е = 10 МПа, определить коэффициент вязкости.

«136. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Для второго материала, модуль упругости которого равен Е = 20 МПа, определить коэффициент вязкости. 137. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Для третьего материала, модуль упругости которого равен Е = 20 МПа, определить коэффициент вязкости.

« 138. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Для первого материала, коэффициент вязкости которого η = 120 МПа_*с, определить модуль упругости Е.

«139. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Для второго материала, коэффициент вязкости которого η = 40 МПа_*с, определить модуль упругости Е.

140. На рис. 8 представлены кривые релаксации напряжения для трех различных материалов. Для третьего материала, коэффициент вязкости которого η = 50 МПа_*с, определить модуль упругости Е.

Биоакустика

1. Приведите классификацию различных видов колебательных движений.

2. Дайте определение основных характеристик колебательного движения (периода, амплитуды, частоты, фазы).

3. Запишите дифференциальное уравнение свободных незатухающих колебаний. Поясните физический смысл, входящих в него величин

4. Запишите дифференциальное уравнение свободных затухающих колебаний. Поясните физический смысл, входящих в него величин.

5.Запишите дифференциальное уравнение вынужденных колебаний. Поясните физический смысл, входящих в него величин.

6.Запишите решение дифференциального уравнения свободных незатухающих колебаний. Поясните физический смысл, входящих в него величин.

7.Запишите решение дифференциального уравнения свободных затухающих колебаний. Поясните физический смысл, входящих в него величин.

8.Запишите решение дифференциального уравнения вынужденных колебаний. Поясните физический смысл, входящих в него величин.

9.Во сколько раз изменилась энергия гармонических колебаний, если частота их возросла в

3 раза, а амплитуда в 4 раза?

10.Какие энергетические процессы происходят при колебаниях. Приведите соответствующие примеры.

11.Дате определение механической волны и запишите ее уравнение.

12.В чем отличие продольных волн от поперечных? Приведите примеры таких волн

13.Каким волнам продольным или поперечным присуще явление поляризации?

14.Как связаны между собой скорость распространения волны, ее длина волны и частота?

15.Перечислите объективные основные характеристики звука.

16.Перечислите субъективные основные характеристики звука.

17.Что называется аудиометрией?

18.Перечислите основные методы звуковой и ультразвуковой диагностики

19.Перечислите основные методы воздействия ультразвука на организм.

20.Дайте определение единицы шкалы уровня интенсивности звука.

21.Дайте определение единицы шкалы уровня громкости звука.

22. Уравнение колебаний имеет вид: 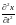+ 4 + 36 Х = 10 cos(8 t) .

Чему равны: а) частота собственных колебаний? б) установившаяся частота колебаний?

23.В выражении для смещения гармонического колебания: Х = 20 cos (62.8 t + /4).

Определите амплитуду, период, частоту и начальную фазу колебаний.

2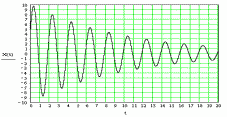 4. На рис. 1 представлен график затухающих колебаний. Х= А _*exp (-  _*t) cos( _*t +  ₀)

Рис. 1

Определить начальную фазу колебаний.

25. Рис. 1. Определить период колебаний

26. Рис. 1. Определить частоту колебаний.

27. Рис. 1. Определить круговую частоту колебаний.

28. Рис. 1. Определить коэффициент затухания.

29. Рис. 1. Определить логарифмический декремент затухания.

30. На рис. 2 представлен результат сложения двух гармонических колебаний, направленных по

одной прямой с близкими частотами (биения), совпадающими по фазе.

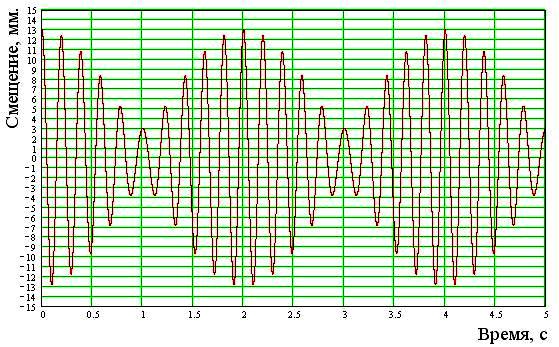
Определить период биения.

31. Рис. 2. Определить частоту биения.

32. Рис. 2. Определить амплитуды складываемых колебаний.

33. Рис. 2. Определить возможные частоты складываемых колебаний.

34. Чему равен логарифмический декремент затухания, если значения амплитуд,

измеренных через период равны 16 см и 5 см.?

35.Чему равен коэффициент затухания колебаний с частотой 4 Гц, если логарифмический декремент затухания  = 5?

36.Коэффициент затухания равен β = 0,04 ,1/с. За какое время амплитуда колебаний

уменьшилась в "е" раз.

37.Уравнение колебаний имеет вид: + 4 + 36 Х = 0 .

Чему равен коэффициент затухания β?

38.Для затухающих колебаний смещение описываются уравнением:

Х = 15 exp (-100 t) cos (62,8 t + /4) . Определите логарифмический декремент затухания.

39 .За 30с амплитуда уменьшилась в 10 раз. Чему равен коэффициент затухания?

40.За один период амплитуда снизилась на 30%. На сколько % она снизится за 3 периода?

41.Логарифмический декремент затухания колебаний маятника равен 0,005. Определите число полных колебаний, которое должен сделать маятник, чтобы амплитуда колебаний уменьшилась в 3 раза.

42.Амплитуда колебаний маятника уменьшается в 10 раз за 30 полных колебаний. Определите логарифмический декремент затухания.

43.Амплитуда колебаний маятника уменьшается в 20 раз за 200 полных колебаний. Определите коэффициент затухания, если период колебаний равен 5 с.

44.Колебательное движение материальной точки задано уравнением:

Х = 12 cos[0,63 (t + 0,5)] . Определите максимальное ускорение колеблющейся точки. Х - в миллиметрах, t - в секундах.

45.На пружине подвешен шарик массой m = 50 г, радиусом R = 5 мм. Он совершает затухающие колебания в широком и глубоком сосуде с ньютоновской жидкостью. За время t = 15 с амплитуда колебаний уменьшилась в 5 раз. Определите коэффициент вязкости жидкости.

46.Во сколько раз изменился модуль вектора Умова, если амплитуда волны уменьшилась в 3 раза, частота возросла в 4 раза, скорость распространения увеличилась в 2 раза?

47.Энергия волны E= 5 Дж переносится в течение t = 5 с через перпендикулярную волне площадку площадью S = 2 см ² . Чему равна интенсивность волны I (Вт/ м ²)?

48. Мощность ультразвукового импульса, посылаемого диагностическим прибором N= 15 мВт. Определите амплитуду X₀ ультразвуковой волны в точке, где площадь поперечного сечения конуса излучения равна S=10 см ².Скорость распространения ультразвука в тканях

V= 1500 м/с. Рабочая частота зонда прибора ν =10 МГц. Средняя плотность тканей

ρ = 1100 кг/м ³. Поглощением ультразвука пренебречь.

49. Мощность ультразвукового импульса, посылаемого диагностическим прибором равна

N=25 мВт. Определите интенсивность I ультразвуковой волны в точке, где площадь поперечного сечения конуса излучения S= 5 см.²

50. Звуковая волна с уровнем интенсивности L = 60 ,дБ попадает на барабанную перепонку площадью S = 50 мм ² и полностью поглощается. Определите энергию E, которую поглощает барабанная перепонка в одну секунду.

51.Определите уровень интенсивности L, дБ звуковой волны в воздухе, который соответствует амплитуде смещения колеблющихся молекул воздуха X₀ =2 мкм при частоте 200 Гц. Плотность воздуха принять равной ρ = 1,3 кг/м³, а скорость звука в воздухеV = 330 м/с.

52. У диагностического ультразвукового прибора имеется зонд с рабочей частотой 15 МГц. Определите теоретический предел разрешения данного прибора, приняв скорость распространения ультра звука в мягких тканях равной V = 1500 м/с.

53.При определении скорости кровотока доплеровское смещение частоты составило

∆ν/ν = 0,06%. Определите скорость крови, если скорость ультразвука в ней V= 1500 м/с.

54.Эритроцит движется в потоке крови со скоростьюV = 300 мм/с. На него падает и затем отражается ультразвуковая волна от неподвижного источника (зонда), работающего на частоте 5 МГц. Определите разность частот ∆ν между отраженной эритроцитом и излучаемой источником ультразвуковыми волнами, если эритроцит удаляется от источника. Скорость распространения ультразвука в крови принять V = 1500 м/с.

55.Эритроцит движется в потоке крови со скоростьюV= 200 мм/с. На него падает и затем отражается ультразвуковая волна от неподвижного источника, работающего на частоте 6 МГц. Определите разность частот ∆ν между отраженной эритроцитом и излучаемой источником ультразвуковыми волнами, если эритроцит приближается к источнику. Скорость распространения ультразвука в крови принять V= 1500 м/с.

56. Звук, какого уровня громкости E ,фон услышит человек, если на него падают звуковые волны с  = 1000 Гц и интенсивностью 10 ^{- 10} Вт /м ²?

57. На сколько фонов изменится уровень громкости звука частотой 1000 Гц, если

интенсивность звука возросла с 10 ^{- 8} Вт/ м ² до 10 ^{- 3} Вт/ м ²?

58.Уровень громкости звука одного человека на частоте 1000 Гц равен 40 фон.

Какой уровень громкости звука создадут 30 одновременно говорящих людей?

59. Уровень интенсивности звука при стрельбе из одного автомата L = 100 дБ.

Определите уровень интенсивности звука L ,дБ при стрельбе из 5 автоматов.

60.Одиночный комар, находящийся на расстоянии 10 м от человека, создает звук,

близкий к порогу слышимости на частоте 1000 Гц. Какой уровень громкости E ,фон

создадут 5000 комаров, находящихся на таком же расстоянии?

61.Работа стоматологической турбины сопровождается шумом с уровнем громкости 35 фон. Компрессор слюноотсоса создает шум с уровнем громкости 40 фон. Определите уровень громкости в фонах, который сопровождает одновременную работу турбины и слюноотсоса. (= 1000 Гц).

62. Потеря слуха у пациента на частоте 1 кГц составляет ∆L= 30 дБ. Определите минимальную интенсивность I волны, которая на это частоте вызывает у пациента ощущение звука.

63. Ухо человека воспринимает разницу уровней громкости на частоте 1000 Гц в 1,0 фон. Определите отношение интенсивностей I₁/ I₂ двух звуковых волн, уровни громкости которых различаются на эту величину.

64. На сколько фон изменится уровень громкости звука частотой 1000 Гц, если

интенсивность звука возросла с 10 ^{- 8} Вт/м ² , до 10 ^{- 2} Вт/м ².

65. Чему равно отношение интенсивностей звука, если различие в уровнях интенсивностей равно 40 дБ?

66. На рис. 3 представлены кривые равной громкости.

Рис. 3

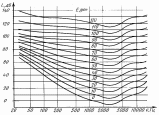
Определить уровень громкости E,фон на частоте 500 Гц при его уровне интенсивности L=20 дБ.

67. Рис. 3. Определить уровень громкости E,фон на частоте 50 Гц при его уровне интенсивности L= 70 дБ.

68. Рис.3. Определить уровень громкости E,фон на частоте 200 Гц при его уровне интенсивности L= 40 дБ.

69. Рис.3. Определить уровень громкости E,фон на частоте 100 Гц при его уровне интенсивности L= 60 дБ.

70. Рис.3. Определить уровень интенсивности L,дБ на частоте 200 Гц при его уровне громкости E= 20 фон

71. Рис.3. Определить уровень интенсивности L, дБ на частоте 500Гц при его уровне громкости E= 10 фон

72. Рис. 3. Определить уровень интенсивности L, дБ на частоте 50 Гц при его уровне громкости E= 30 фон

73. Рис.4 Представлен бланк аудиограммы левого и правого уха, снятой у некоторого пациента. Рис. 4

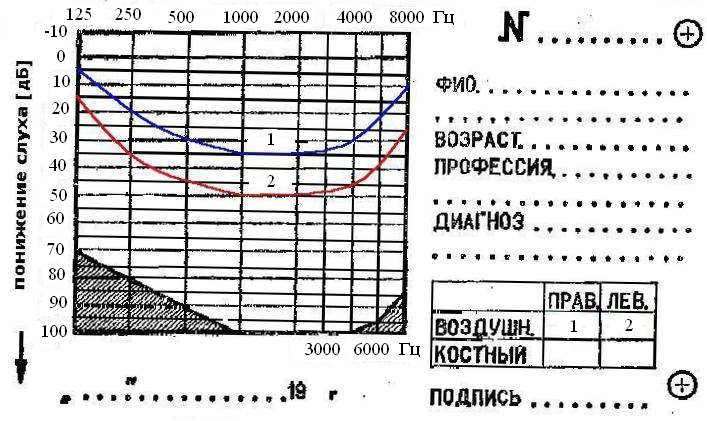
Найти минимальную интенсивность звука I ,Вт/м ², которую пациент услышит своим

правым ухом на частоте 500 Гц

74. Рис.4. Найти минимальную интенсивность звука I ,Вт/м ², которую пациент услышит своим

правым ухом на частоте 1000 Гц

75. Рис. 4. Найти минимальную интенсивность звука I ,Вт/м ², которую пациент услышит своим

правым ухом на частоте 8000 Гц

76. Рис. 4. Найти минимальную интенсивность звука I ,Вт/м ², которую пациент услышит своим

левым ухом на частоте 8000 Гц

77. Рис. 4. Найти минимальную интенсивность звука (Вт/м ²), которую пациент услышит своим

левым ухом на частоте 4000 Гц

78. Рис. 4. Найти минимальную интенсивность звука (Вт/м ²), которую пациент услышит своим

левым ухом на частоте 250 Гц

Эталоны ответов

Биомеханика

021	50 мм	059	Пластическое
022	1	060	6 мкм
023	16,7	061	12 мкм
024	500 МПа	062	12 мкм
025	0,176	063	0,42 МПа
026	12500 МПа	064	0,71 МПа
027	40 МН/м	065	2
028	3,1 МН/м	066	0,25
029	32 МН/м	067	3
030	3,3 МН/м	068	0,5
031	11,4 МН/м	069	10 c
032	1,67 МН/м	070	1 c
033	6,67 МН/м	071	100 с
036	0,24	072	10 5 с
037	0,375	073	10 с
038	1,77	074	10 15 с
039	1,256	075	10 8 с
040	25 МПа	076	100 с
041	2,27	077	10 14 с
042	115,38 ГПа	078	10 6 с
043	212,8 ГПа	079	220 МПа
044	320 Н	080	0 - 0,4 ε
045	400 Н	081	300 МПа
046	300 Н	082	1,36
047	600 Н	083	2,2
048	3,6 Н*м	084	30 см
049	4,2 Н*м	085	88 см
050	4 см	086	0,3
051	1,6 см ; 4,86 см	087	111 МПа
052	Пластическое	088	24 МДж/м 3
053	Хрупкое	089	1,83
054	1 МПа	090	04 ε
055	2 МПа	091	3
056	3 МПа	092	480 Дж
057	120 К	093	1,4
058	120 К	094	162,2 МПа

Гемодинамика и биореология

017	1	065	39	113	5,82 с
018	3,73 с	066	N	114	50 кПа*с
019	1,25 мм	067	X/5	115	19,95 кПа
020	12 см/с	068	2,81	116	24,9 кПа
021	0,07 см/с	069	300 Па	117	5,9
022	79,6 мм/с	070	1,73	118	3 c
023	3066,4 см2	071	0,05	119
024	5,625	072	3,75 мПа*с	120	90 кПа*с
025	41,67 см/с	073	2	121	50 кПа
026	50,7 см/с	074	46,7 см	122
027	96875 Па	075	39,9 Па	123
028	1620 Па	076	2400 1/с	124
029	98420 Па	077	8 мкДж	125	10 с
030	95500 Па	078	4,2	126	100 МПа*с
031	395,1 Па	079	3442	127	400 МПа*с
032	3920 Па	080	1590 ламин.	128	600 МПа*с
033	43945,3 Па	081	33 см/с	129	4 МПа
034	8125 Па	082	285,7 мПа*с	130	5 МПа
035	95500 Па	083	3,98 мПа*с	131	3 МПа
036	8919,8 Па	084	1,05 мПа*с	132	16 с
037	0,075 см/с	085	0,3	133	10 с
038	3,375 c	086	4 мПа*с	134	6 с
039	3,2 мл	087	117 мПа*с	135	160М Па*с
040		088	34 мПа*с	136	200 МПа*с
041	1,58	089	5,6 мПа*с	137	120 МПа*с
042	2,35 мм	090	22,5 мП*с	138	7,5 МПа
043	3,54 мм.	091	13 мПа	139	4 МПа
044	Увел. В 24 раза	092	4,225 мПа	140	8,3 МПа
045	7,72	093	6,4 мПа	141
046	0,84	094	0,24
047	10,61мм	095	0,073
048	12,73 мм	096	55 мПа*с
049	2,81 Па*с	097	24 мПа*с
050	0,4 л/с	098	2,29
051	4*10 7 Па*с/м 3	099	6
052	5*10 7 Па*с/м 3	100	120 мПа
053	2,5	101	195510 кПа
054	1*10 7 Па*с/м 3	102	134,4 кПа
055	31,25 см/с	103	1Дж;3,3 Вт
056	46,88 см/с	104	1Па
057	5/6	105	09
058	3	106	1,25 1/с
059	3,125 Па*с	107	6
060	15,7 Па*с	108	0,8
061	2,62 Па*с	109	30 кПа*с
062	4,55 %	110	0,6
063	- 13,46 %	111	258 мПа
064	26,5 %	112	2 кПа

Биоакустика

22	3/π; 4/π	51	17,3 дБ
23	20; 0,1 c;10 Гц; π/4	52	10 – 4 м
24	π/3	53	0,45 м/с
25	2 c	54	- 1,3 кГц
26	0,5 1/c	55	800 Гц
27	3,14 рад/с	56	20 фон
28	0,11 1/с	57	50 фон
29	0,22	58	56 дБ
30	2 c	59	110,7 дБ
31	0,5 1/c	60	38 фон
32	8 мм и 5 мм	61	41,2 дБ
33	5 Гц и 4,5 Гц; 5 Гц и 5,5 Гц	62	10 – 9 Вт/м 2
34	1,16	63	1,26
35	5/4 1/с	64	60 фон
36	25	65	10 4
37	2 1/с	66	10 фон
38	1	67	30 фон
39	0,076	68	20 фон
40	65 %	69	30 фон
41	220	70	40 дБ
42	0,076	71	20 дБ
43	0,013 1/с	72	70 дБ
44	4,76 мм/с 2	73	10 – 8 Вт/м 2
45	0,114 Па*с	74	10 – 8, 5 Вт/м 2
46	3,56	75	10 – 9, 5 Вт/м 2
47	5 кВт/м 2	76	10 – 8 Вт/м 2
48	6,79*10 – 11 м	77	10 – 7, 5 Вт/м 2
49	50 Вт/м 2	78	10 – 6, 5 Вт/м 2
50	50*10 -12 Дж

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

МЕДИКО-СТОМАТОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА

Медицинской и биологической физики

А.А. Синицын, В.С. Воеводский, В.М.Говорун

Вопросы и задачи

к экзамену по медицинской и биологической

физике для студентов стоматологического и лечебного факультетов