5.3.2Логарифмическая амплитудно-фазочастотная характеристика

Логарифмическая амплитудно-фазочастотная характеристика замкнутой системы определяется на основании (5.15):

(5.1296)

где L,  - ЛАФЧХ разомкнутой системы с единичной обратной связью, или поправки по амплитуде и фазе.

Логарифмическая амплитудно-фазочастотная характеристика замкнутой системы может быть построена тремя способами:

- аналитически по выражению (5.16),

- упрощенным или аппроксимированным методом, для оценки формы ЛАФЧХ,

- с помощью номограмм замыкания.

Пример построения с аналитическим методом будет показан ниже.

5.3.3 Упрощенное (аппроксимированное) построение замкнутой лафчх

АФЧХ замкнутой системы (5.15) имеет вид :

.

а) Пусть в некотором диапазоне частот:

. (5.130)

Тогда единицей в знаменателе можно пренебречь, и уравнение (5.16) запишется так:

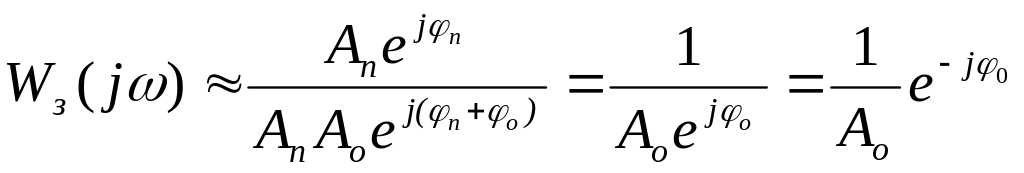. (5.131)

При этом эквивалентная ЛАФЧХ замкнутой системы будет примерно равна:

(5.132)

б) Пусть в другом диапазоне частот:

. (5.133)

Следовательно, выражением в знаменателе можно пренебречь, и уравнение (5.16) примет вид:

. (5.134)

При этом эквивалентная ЛАФЧХ замкнутой системы будет примерно равна:

(5.135)

На основании этого можно сделать вывод, что эквивалентную замкнутую ЛАЧХ можно заменить аппроксимированной, которую проводят по наименьшей между ЛАЧХ прямого канала (L_п) и обратной канала обратной связи (–L₀) _.

в) Наибольшая погрешность такого метода будет иметь место, очевидно, в диапазоне частот, в котором A_пA_o1. Оценим максимальную погрешность аппроксимации. Знаменатель передаточной функции (5.16) при условии A_пA_o1 можно представить следующим образом:

.

Максимальное значение знаменателя в этом диапазоне частот будет равно 2 (при =0). Следовательно, согласно (5.16) АЧХ замкнутой системы будет отличаться от АЧХ прямого канала или канала обратной связи не более, чем в два раза. В логарифмическом масштабе разница будет составлять не более 6 дБ.

Алгоритм построения аппроксимированной замкнутой ЛАФЧХ:

1) строятся ЛАФЧХ прямого канала L_п, _п и ЛАФЧХ канала обратной связи L_о, _о;

2) строятся обратные характеристики канала обратной связи –L_o, _о путем зеркального отражения характеристик L₀, φ₀ относительно горизонтальной оси lg.

3) логарифмическая характеристика замкнутой системы строится «по низам» между L_п и L_о;

4) фазочастотная характеристика строится по частям _п и _о, в диапазонах частот, соответствующим частям ЛАЧХ, входящим в эквивалентную ЛАЧХ.

Пример построения аппроксимации будет показан ниже.