МЕТОДЫ ПОДОБИЯ И РАЗМЕРНОСТИ

Подобие гидродинамических движений

В механике жидкости есть несколько известных точных решений

уравнений движения вязкой жидкости. Можно было бы указать еще

несколько примеров и тем самым исчерпать весь список имеющихся точных решений. Однако практика настоятельно требует решения

задач, которые, в силу математических трудностей, не могут быть

решены аналитически точно. В этих многочисленных случаях нам

необходимо обращаться непосредственно к эксперименту. Но и экспериментальные данные не всегда возможно получить на тех объектах,

для которых решается данная задача.

Например, мы хотели бы знать силу сопротивления, которую испытывает новая, проектируемая конструкция самолета при движении его

с заданной скоростью на определенной высоте. Зная силу сопротивления, мы могли бы выбрать двигатель, обеспечивающий требуемые

характеристики полета. Вообще говоря, можно изготовить полностью

такой самолет, поставить на него некоторый двигатель и, поднявшись

на заданную высоту, измерить скорость. Но ведь установленный двигатель может и не развить заданную скорость, а в распоряжении

конструктора сегодня может и не оказаться подходящего двигателя.

В принципе методом проб и ошибок можно было бы каким-либо компромиссным способом проблему все же решить, однако такой путь

связан с большими материальными и временными затратами. То же

самое можно было бы сказать о проблемах проектирования больших

турбин, судов, ракет и т.д.

Поэтому, конечно, было бы заманчивым проводить опыты на

небольших моделях реальных объектов в условиях, полностью подчиняющихся и контролируемых экспериментатором. Однако возникает

существенный вопрос, в какой мере, когда и как возможно результаты,

полученные на моделях, применять к натурным объектам. На этот

вопрос отвечает теория подобия гидродинамических движений.

Безразмерные уравнения движения.

Рассмотрим уравнение Навье-Стокса. В качестве объемной силы рассмотрим силу тяжести: (1)

Для не очень быстрых движений объемная вязкость несущественна

и мы будем полагать ее равной нулю. Кроме того, для простоты будем

полагать движение изотермическим, тогда уравнение баланса внутренней энергии можно не рассматривать.

Приведем уравнения движения к безразмерному виду. Для этого

выберем некоторые характерные размерные величины. Пусть L — некоторый характерный размер обтекаемого тела (диаметр шара, трубы,

большая ось эллипса, хорда профиля крыла и т.д.). Тогда размерные

декартовы координаты можно записать в виде

Здесь— некоторые безразмерные координаты. Не сложно догадаться, что мы масштабируем все расстояние, которые теперь измеряются в долях расстояние L

Далее у нас есть - скорость набегающего потока жидкости или скорость в центре трубы и т.д. Тогда для размерной скорости жидкости в любой точке потока можно записать её скорость:

где — безразмерная скорость движения жидкости.

Для нестационарных задач выберем также некоторое характерное

время , которое может быть или периодом движения для периодических движений, или временем релаксации потока к стационарному

движению, или просто временем прохождения выбранного расстояния

с выбранной безразмерной скоростью . Переход к безразмерному времени аналогичен .

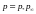
Принимая за характерное давление и плотность, например, давление и плотность в набегающем потоке, имеем , где -ускорение свободного падения.

Получим следующие члены уравнения:

(2)

Методы подобия и размерности

Подставляя полученные соотношения в уравнение Навье-Стокса (1)

и деля на коэффициент при конвективном члене , получим

(3)

Аналогично можно записать уравнение неразрывности в безразмерном

виде я

|^ + ^div»(p*v»)=0. G.9)

При изотермическом движении уравнение состояния для идеального газа (закон Бойля-Мариотта) будет иметь вид

^= const*. G.10)

Р*

Обозначим безразмерные коэффициенты уравнений G.8), G.9) следующим образом:

L Poo ^

Тогда любое решение системы уравнений G.8)—G.10) независимо

от формы движения жидкости будет иметь вид

v#i=*- = /(st, M, Re, Fr, х*, у*, z*, U). G.12)

Аналогичные выражения можно записать для безразмерных величин давления и плотности.

Из G.12) следует, что в двух потоках жидкости, для которых одинаковы безразмерные коэффициенты St, M, Re, Fr, в сходственных точках

(одинаковые ж*, у*, z*) в сходственные моменты времени (одинаковые

t*) безразмерные скорости, давления и плотности будут равны. Такие

потоки называются динамически подобными.

Поэтому два изотермических потока жидкости будут динамически подобны, если выполняются, прежде всего, следующие равенства:

Sti=St2, Mi = M2, Rei = Re2, Fri = Fr2 . G.13)

Эти безразмерные коэффициенты называются критериями или числами динамического подобия потоков:

St — число Струхала , Re — число Рейнольдса,

М — число Маха (Маиевского), Fr — числе Фруда.

Нетрудно видеть, что динамически подобными могут быть лишь

потоки, обтекающие геометрически подобные тела, одинаково расположенные к направлению набегающего потока. Геометрически подобные

тела — это такие тела, для любых сходственных точек поверхности

которых их безразмерные координаты одинаковы, если за характерный