Проверка гипотез нормальности распределения
Существует несколько методик проверки гипотезы нормальности распределения. Рассмотрим некоторые из них.
Методика по среднему абсолютному отклонению.
Эта методика приспособлена
для не очень больших выборок (
).
Здесь вычисляется среднее абсолютное
отклонение -
.
Для выборки, имеющей приближенно
нормальный закон распределения, должно
быть справедливо соотношение
.
В нашем случае
,
.
И, таким образом, гипотеза нормальности исследуемого распределения по этой методике принимается.
2. Методика по размаху варьирования R .
Она применима для
широкого класса выборок
.
Здесь подсчитывают отношение
и сопоставляют его с критическими
верхней и нижней границами этого
отношения, приведенными в таблице
приложения 2 настоящего пособия. Если
вычисленное отношение
находится в указанной вилке, то гипотеза
о нормальном распределении принимается.
В противном случае нормального
распределения нет.
В нашем случае
.
При
и
(10% уровень значимости(вероятность
ошибки)) нижняя граница Н.Г.= 4,03,
верхняя граница В.Г.= 5,23. Следовательно,
и т.о. гипотеза нормальности распределения
подтверждается и по этому критерию.
П
2. Критические границы отношения
*
Объем |
Нижние границы |
Верхние границы |
|
||||||||||||||||||||||
выбор- |
Вероятность ошибки |
|
|||||||||||||||||||||||
ки n |
0,000 |
0,005 |
0,01 |
0,025 |
0,05 |
0,10 |
0,10 |
0,05 |
0,025 |
0,01 |
0,005 |
0,000 |
|
||||||||||||
3 |
1,732 |
1,735 |
1,737 |
1,745 |
1.758 |
1,782 |
1,997 |
1,999 |
2,000 |
2,000 |
2,000 |
2,000 |
|||||||||||||
4 |
1,732 |
1,83 |
1,87 |
1,93 |
1,98 |
2,04 |
2,409 |
2,429 |
2,439 |
2,445 |
2,447 |
2,449 |
|||||||||||||
5 |
1,826 |
1,98 |
2,02 |
2,09 |
2,15 |
2,22 |
2,712 |
2,753 |
2,782 |
2,803 |
2,813 |
2,828 |
|||||||||||||
6 |
1,826 |
2,11 |
2,15 |
2,22 |
2,28 |
2,37 |
2,949 |
3,012 |
3,056 |
3,095 |
3,115 |
3,162 |
|||||||||||||
7 |
1,871 |
2,22 |
2,26 |
2,33 |
2,40 |
2,49 |
3,143 |
3,222 |
3,282 |
3,338 |
3,369 |
3,465 |
|||||||||||||
8 |
1,871 |
2,31 |
2,35 |
2,43 |
2,50 |
2,59 |
3,308 |
3,399 |
3,471 |
3,543 |
3,585 |
3,742 |
|||||||||||||
9 |
1,897 |
2,39 |
2,44 |
2,51 |
2,59 |
2,68 |
3,449 |
3,552 |
3,634 |
3,720 |
3,772 |
4,000 |
|||||||||||||
10 |
1,897 |
2,46 |
2,51 |
2,59 |
2,67 |
2,76 |
3,57 |
3,685 |
3,777 |
3,875 |
3,935 |
4,243 |
|||||||||||||
11 |
1,915 |
2,53 |
2,58 |
2,66 |
2,74 |
2,84 |
3,68 |
3,80 |
3,903 |
4,012 |
4,079 |
4.472 |
|||||||||||||
12 |
1,915 |
2,59 |
2,64 |
2,72 |
2,80 |
2,90 |
3.78 |
3,91 |
4.02 |
4.134 |
4,208 |
4,690 |
|||||||||||||
13 |
1,927 |
2,64 |
2,70 |
2,78 |
2,86 |
2,96 |
3,87 |
4,00 |
4.12 |
4.244 |
4.325 |
4,899 |
|||||||||||||
14 |
1,927 |
2,70 |
2,75 |
2.83 |
2,92 |
3,02 |
3,95 |
4.09 |
4,21 |
4,34 |
4.431 |
5.099 |
|||||||||||||
15 |
1,936 |
2,74 |
2,80 |
2,88 |
2,97 |
3,07 |
4,02 |
4Л7 |
4,29 |
4,44 |
4,53 |
5.292 |
|||||||||||||
16 |
1,936 |
2,79 |
2,84 |
2,93 |
3,01 |
3,12 |
4,09 |
4,24 |
4,37 |
4.52 |
4,62 |
5,477 |
|||||||||||||
17 |
1,944 |
2,83 |
2,88 |
2,97 |
3,06 |
3,17 |
4,15 |
4,31 |
4.44 |
4,60 |
4.70 |
5.657 |
|||||||||||||
18 |
1,944 |
2,87 |
2,92 |
3,01 |
3,10 |
3.21 |
4,21 |
4,37 |
4,51 |
4.67 |
4,78 |
5,831 |
|||||||||||||
19 |
1,949 |
2,90 |
2,96 |
3,05 |
3,14 |
3,25 |
4,27 |
4,43 |
4.57 |
4,74 |
4,85 |
6,000 |
|||||||||||||
20 |
1,949 |
2,94 |
2,99 |
3,09 |
3,18 |
3,29 |
4,32 |
4,49 |
4,63 |
4,80 |
4.91 |
6,164 |
|||||||||||||
25 |
1,961 |
3,09 |
3,15 |
3,24 |
3,34 |
3,45 |
4,53 |
4,71 |
4.87 |
5,06 |
5.19 |
6,93 |
|||||||||||||
30 |
1,966 |
3,21 |
3,27 |
3,37 |
3,47 |
3,59 |
4,70 |
4,89 |
5.06 |
5,26 |
5,40 |
7.62 |
|||||||||||||
35 |
1,972 |
3,32 |
3,38 |
3,48 |
3,58 |
3,70 |
4.84 |
5.04 |
5,21 |
5,42 |
5,57 |
8.25 |
|||||||||||||
40 |
1,975 |
3,41 |
3,47 |
3,57 |
3,67 |
3,79 |
4,96 |
5,16 |
5,34 |
5,56 |
5,71 |
8.83 |
|||||||||||||
45 |
1,978 |
3,49 |
3,55 |
3,66 |
3,75 |
3,88 |
5,06 |
5,26 |
5,45 |
5,67 |
5,83 |
9,38 |
|||||||||||||
50 |
1,980 |
3,56 |
3,62 |
3,73 |
3,83 |
3,95 |
5,14 |
5.35 |
5.54 |
5,77 |
5.93 |
9,90 |
|||||||||||||
55 |
1,982 |
3,62 |
3,69 |
3,80 |
3,90 |
4,02 |
5.22 |
5,43 |
5.63 |
5,86 |
6.02 |
10,39 |
|||||||||||||
60 |
1,983 |
3,68 |
3,75 |
3,86 |
3,96 |
4.08 |
5,29 |
5,51 |
5.70 |
5,94 |
6,10 |
10.86 |
|||||||||||||
65 |
1.985 |
3,74 |
3,80 |
3,91 |
4,01 |
4,14 |
5,35 |
5.57 |
5,77 |
6,01 |
6,17 |
11.31 |
|||||||||||||
70 |
1,986 |
3,79 |
3,85 |
3,96 |
4,06 |
4,19 |
5,41 |
5,63 |
5,83 |
6,07 |
6.24 |
11,75 |
|||||||||||||
75 |
1,987 |
3,83 |
3,90 |
4,01 |
4,11 |
4,24 |
5,46 |
5,68 |
5,88 |
6,13 |
6,30 |
12.17 |
|||||||||||||
80 |
1,987 |
3,88 |
3,94 |
4,05 |
4,16 |
4,28 |
5,51 |
5,73 |
5,93 |
6,18 |
6.35 |
12.57 |
|||||||||||||
85 |
1,988 |
3,92 |
3,99 |
4,09 |
4,20 |
4,33 |
5.56 |
5,78 |
5,98 |
6.23 |
6,40 |
12.96 |
|||||||||||||
90 |
1,989 |
3,96 |
4,02 |
4,13 |
4,24 |
4,36 |
5.60 |
5,82 |
6,03 |
6,27 |
6,45 |
13.34 |
|||||||||||||
95 |
1,990 |
3,99 |
4,06 |
4,17 |
4,27 |
4,40 |
5,64 |
5,86 |
6,07 |
6,32 |
6.49 |
13.71 |
|||||||||||||
100 |
1,990 |
4,03 |
4,10 |
4,21 |
4,31 |
4,44 |
5,68 |
5,90 |
6.11 |
6,36 |
6.53 |
14.07 |
|||||||||||||
150 |
1,993 |
4,32 |
4,38 |
4,48 |
4,59 |
4,72 |
5,96 |
6,18 |
6,39 |
6,64 |
6.82 |
17.26 |
|||||||||||||
200 |
1,995 |
4,53 |
4,59 |
4,68 |
4,78 |
4,90 |
6,15 |
6,39 |
6,60 |
6.84 |
7.01 |
19.95 |
|||||||||||||
500 |
1,998 |
5,06 |
5,13 |
5,25 |
5,37 |
5,49 |
6,72 |
6,94 |
7.15 |
7.42 |
7.60 |
31.59 |
|||||||||||||
1000 |
1,999 |
5,50 |
5,57 |
5.68 |
5,79 |
5.92 |
7,11 |
7.33 |
7.54 |
7.80 |
7,99 |
44.70 |
|||||||||||||
* Таблица заимствована из [7] , с. 299.
По показателям асимметрии и эксцесса.
Показатель асимметрии
можно определить по формуле
.
Для симметричных распределений
и
.
Для нормального распределения
.
Для сравнения эмпирического распределения
и нормального распределения в качестве
показателя эксцесса принимают величину
.
В рассматриваемом
примере
.
Таким образом, некоторая асимметрия имеется.
,
т.е. имеется и небольшой эксцесс.
Несмещенные оценки для показателей асимметрии и эксцесса определяют по формулам:
,
.
В нашем случае:
,
.
Для проверки гипотезы нормальности распределения необходимо вычислить среднеквадратические отклонения для показателей асимметрии и эксцесса по формулам:
,
.
Если при этом выполняются
условия
,
,
то гипотеза нормальности распределения
может быть принята.
В нашем примере:
;
.
Теперь
,
.
И таким образом, по данному критерию
гипотеза нормальности распределения
так же принимается.
Критерий согласия Пирсона.
По данным наблюдений определяют и .
В
нашем случае
и
.
Находят ординаты - выравнивающие частоты теоретической кривой (такие частоты, которые были бы у распределения, если бы оно было нормально распределено с параметрам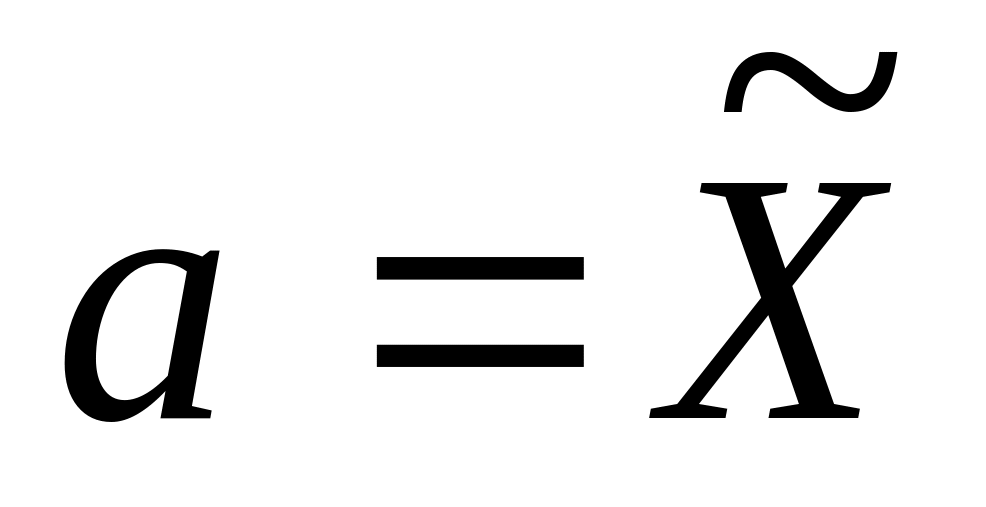и
и
)
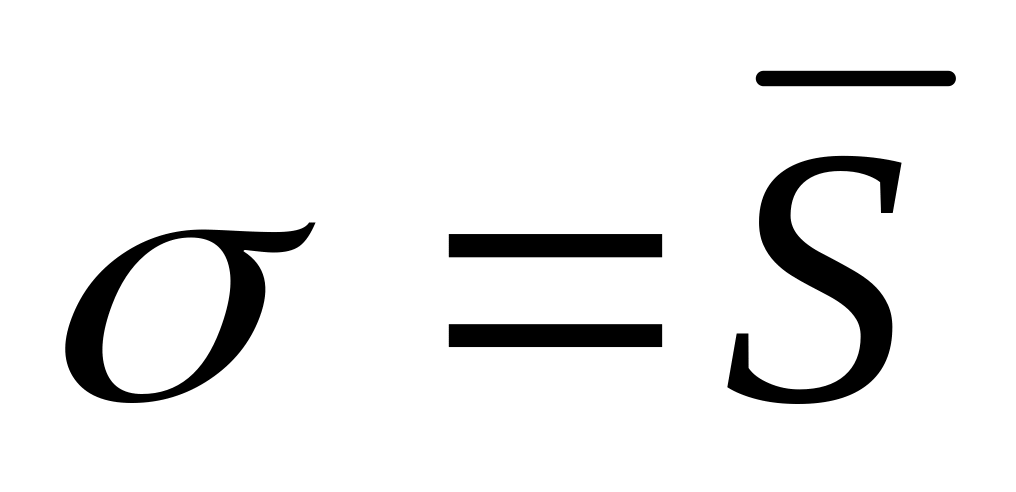по формуле
,
где n
– количество испытаний, h
– разность между двумя соседними
вариантами СВ
Х
(
),
,
.
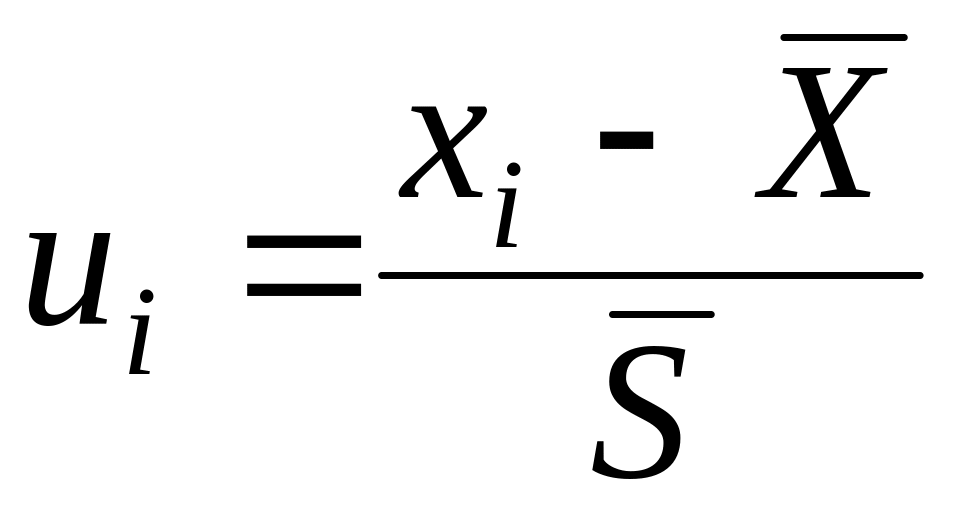В нашем случае сводим проведенные вычисления в таблицу 4.
Таблица 4.
-
167
5
-8,66
-1,56
0,118
4,76
171
13
-4,66
-0,84
0,280
11,30
175
15
-0,66
-0,12
0,396
15,98
179
14
3,34
0,60
0,333
13,44
183
5
7,34
1,32
0,167
6,74
187
4
11,34
2,04
0,050
2,02
Строят точки и в прямоугольной системе координат и соединяют их ломанными кривыми, то есть строят полигоны частот.
Для рассматриваемой задачи полигоны частот приводятся на рис. 6.
Близость выравнивающих частот (штриховая линия) к наблюдаемым в эксперименте частотам (сплошная линия) подтверждает правильность допущения о том, что обследуемый признак распределен нормально.
Возникает вопрос: случайно ли расхождение экспериментальных и выравнивающих теоретических частот или неслучайно? Может быть мало наблюдений? Может быть неверно избран закон распределения? Эти обстоятельства выясняем ниже.
Вычисляется показатель
.
В нашем случае результаты проведенных вычислений приводятся в таблице 5.
Таблица 5.
|
|
|
|
|
5 |
4,76 |
0,24 |
0,0576 |
0,0121 |
13 |
11,30 |
1,7 |
2,89 |
0,2558 |
15 |
15,98 |
-0,98 |
0,9604 |
0,0601 |
14 |
13,44 |
0,56 |
0,3136 |
0,0233 |
5 |
6,74 |
-1,74 |
3,0276 |
0,4492 |
4 |
2,02 |
1,98 |
3,9204 |
1,9408 |
|
|
|
|
|
5.
Вычисляется число степеней свободы
,
где S
– число групп, на которые разбита
выборка.
У
нас
,
.
6. Выбирается уровень значимости для поставленной задачи.
Уровнем значимости называют достаточно малую вероятность, при которой событие можно считать практически невозможным. Насколько малой должна быть вероятность события, чтобы можно было считать невозможным его появление в отдельном испытании можно понять из следующих примеров (примеры опоздания поезда и не раскрытия парашюта).
На практике принимают уровень значимости между 0,01 и 0,05 (однопроцентный и пятипроцентный уровни значимости). Пусть в рассматриваемом примере уровень значимости 0,01.
7.
Ищется по таблице приложения 3, по
найденным значениям
и
,
вероятность
.
Если эта вероятность меньше принятого
уровня значимости, то гипотеза о
нормальном распределении генеральной
совокупности отвергают, если больше –
принимают.
В
нашем случае при
и
.
Таким образом, данные наблюдений согласуются с гипотезой о нормальном распределении рассматриваемой СВ и по критерию Пирсона.
П
3. Закон распределения
k
|
2 |
4 |
6 |
8 |
10 |
12 |
15 |
20 |
25 |
1 |
6065 |
9098 |
9856 |
9982 |
9998 |
10 000 |
10 000 |
10 000 |
10 000 |
2 |
3679 |
7358 |
9197 |
9810 |
9963 |
9 994 |
10 000 |
10000 |
10 000 |
3 |
2231 |
5578 |
8088 |
9344 |
9814 |
9 955 |
9 996 |
10 000 |
10 000 |
4 |
1353 |
4060 |
6767 |
8571 |
9474 |
9 834 |
9 977 |
10 000 |
10 000 |
5 |
821 |
2873 |
5433 |
7576 |
8912 |
9 580 |
9 921 |
9 997 |
10 000 |
6 |
498 |
1992 |
4232 |
6472 |
8153 |
9 161. |
9 798 |
9 989 |
10 000 |
7 |
302 |
1359 |
3208 |
5366 |
7254 |
8 576 |
9 576 |
9 967 |
9 998 |
8 |
183 |
916 |
2381 |
4335 |
6288 |
7 851 |
9 238 |
9919 |
9 995 |
9 |
111 |
611 |
1736 |
3423 |
5321 |
7 029 |
8 775 |
9 829 |
9 986 |
10 |
67 |
404 |
1246 |
2650 |
4405 |
6 160 |
8 197 |
9 682 |
9 966 |
12 |
25 |
174 |
620 |
1512 |
2851 |
4 457 |
6 790 |
9 161 |
9 866 |
14 |
9 |
73 |
296 |
818 |
1730 |
3 007 |
5 255 |
8 305 |
9 617 |
16 |
3 |
30 |
138 |
424 |
996 |
1912 |
3 821 |
7 166 |
9 148 |
18 |
1 |
12 |
62 |
212 |
550 |
1 157 |
2 627 |
5 874 |
8 421 |
20 |
0 |
5 |
28 |
103 |
292 |
671 |
1719 |
4 579 |
7 468 |
25 |
|
1 |
3 |
16 |
54 |
148 |
499 |
2014 |
4 624 |
30 |
|
0 |
0 |
2 |
9 |
28 |
119 |
698 |
2 243 |
В
таблице приведены значения
.
Нами рассмотрены четыре методики проверки нормальности распределения: по САО, по размаху варьирования R, по показателям асимметрии и эксцесса, критерий Пирсона. Существует ряд других методик. Для практического применения рекомендуем в основном две методики: по размаху варьирования R и с использованием критерия Пирсона. Причем первая из них служит для быстрой прикидочной проверки, а вторая – для основательной проверки нормальности распределения. Оба критерия могут быть легко реализованы с использованием калькуляторов.