Характеристики генеральной совокупности
Пусть ряд распределения дискретной генеральной совокупности
-
Х
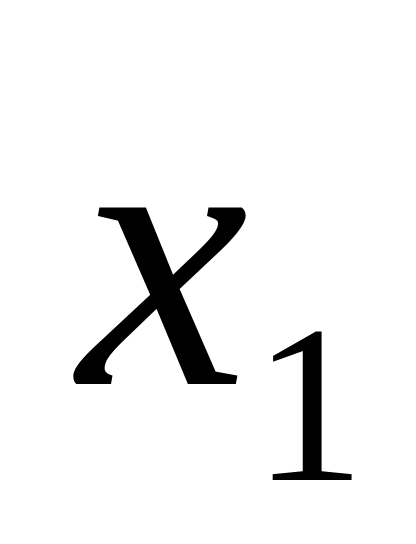
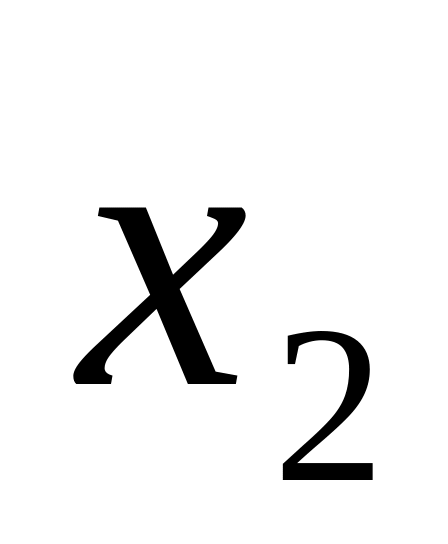
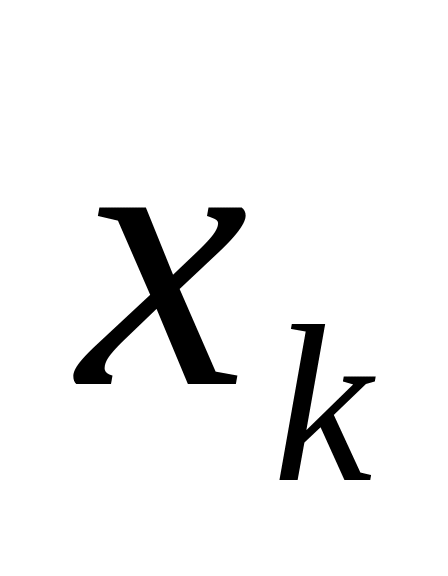
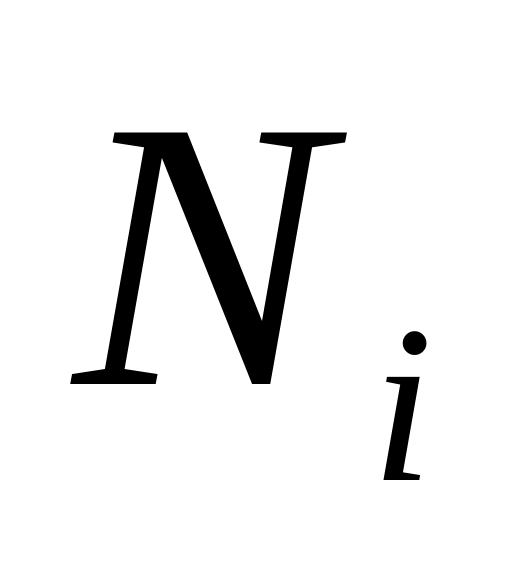
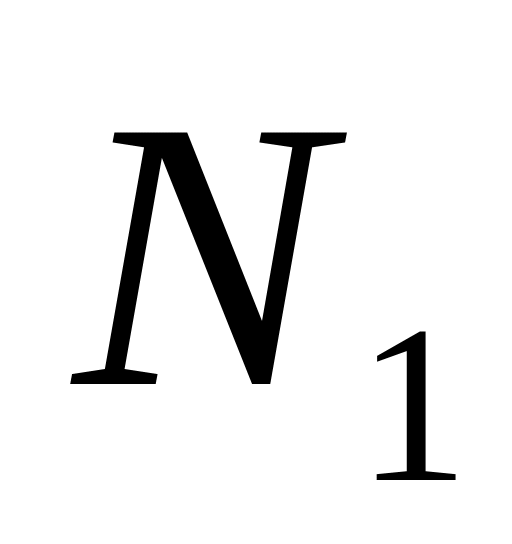
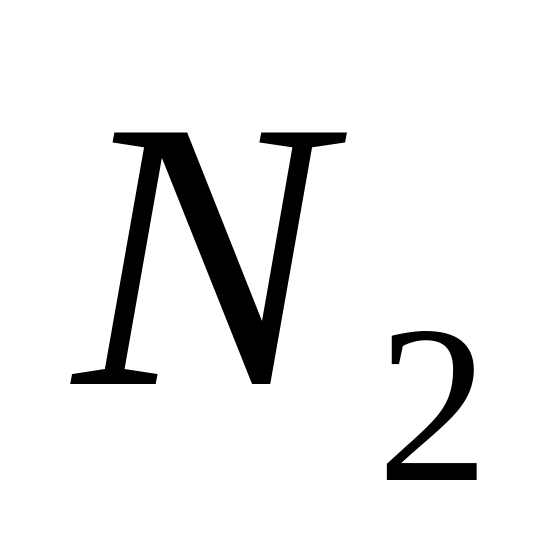
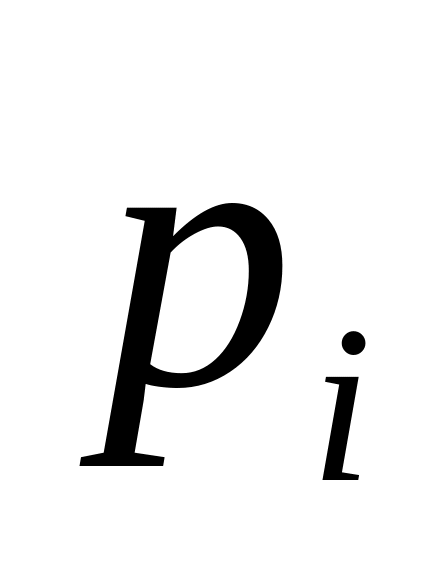
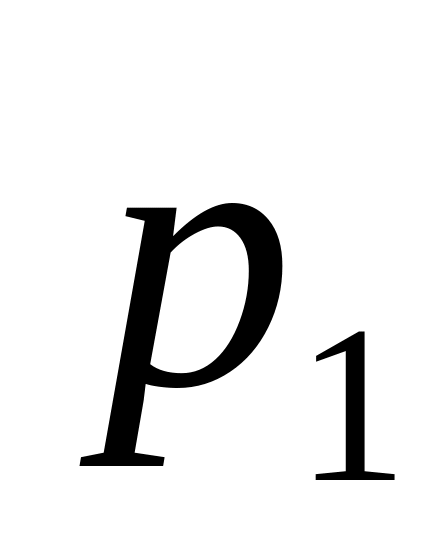
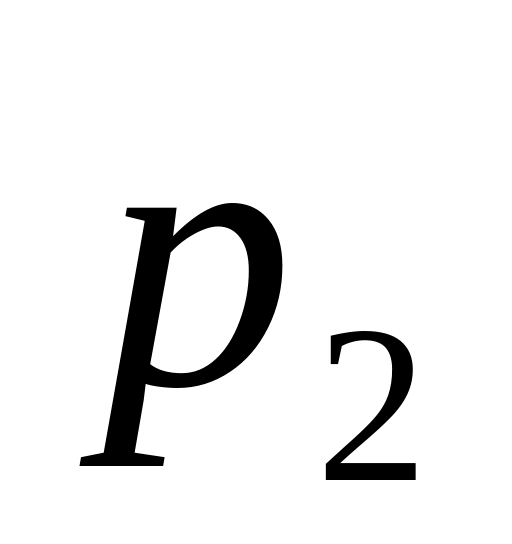
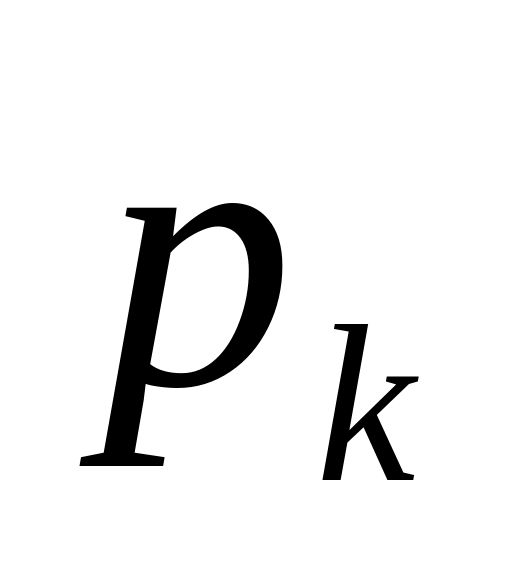
где
-
число значений
,
принятых случайной величиной Х,
- вероятность появления признака
,
- объем генеральной
совокупности.
Математическое ожидание генеральной совокупности:
.
Дисперсия генеральной совокупности:
.
Среднее
квадратическое отклонение
генеральной
совокупности (стандарт):
.
Характеристики статистического ряда
Пусть из генеральной совокупности сделана выборка объема n и ее статистический ряд:
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
Здесь - значение величины Х, наблюдаемое в i – том опыте, n – число опытов.
Математическое
ожидание (выборочная средняя)
случайной величины Х:
.
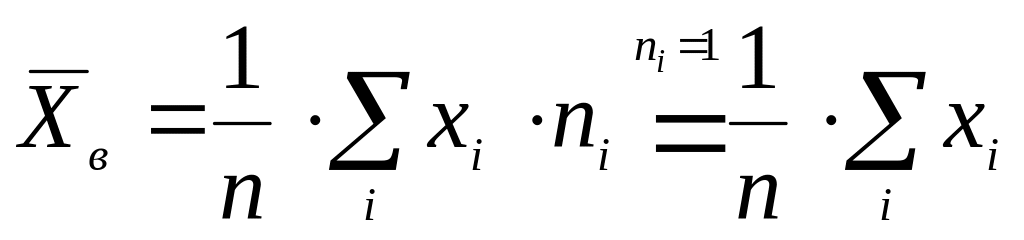Дисперсия выборки:
.
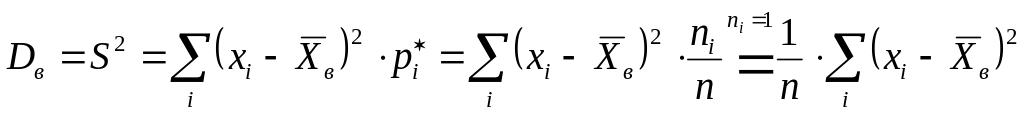Выборочное
среднее квадратическое отклонение:
.
Размахом
вариации (размахом вариационного ряда)
называется число
,
где
и
-
соответственно наибольший и наименьший
варианты ряда.
Модой вариационного ряда называется вариант ряда имеющий наибольшую частоту.
Медианой вариационного ряда называется значение признака (СВ Х), приходящееся на середину ряда.
Статистические оценки параметров распределения
Требуется
изучить некоторый количественный
признак генеральной совокупности.
Предположим, что удалось установить
каков закон распределения исследуемого
признака. Возникает задача оценки
параметров (мат. ожидания - а
и с.к.о. -
в случае нормального распределения СВ
Х, параметра-
в случае закона Пуассона
),
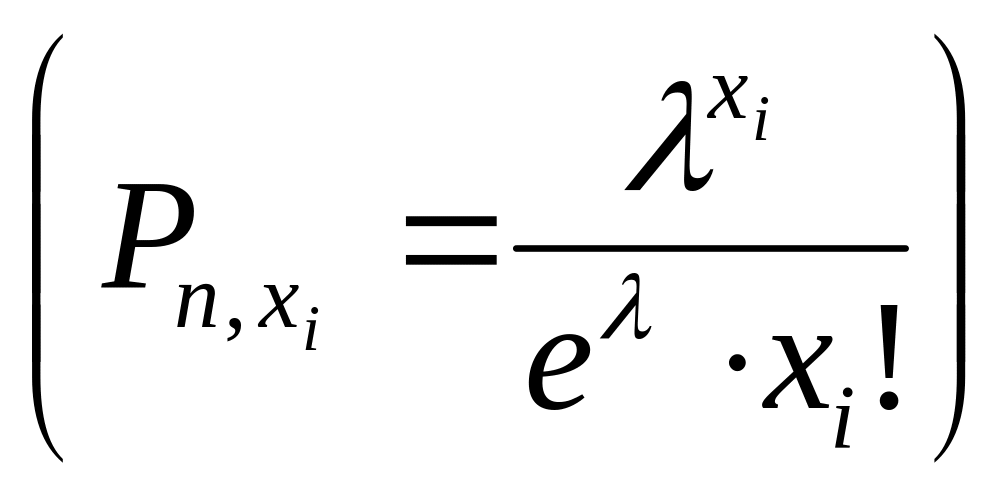которыми определяется
распределение генеральной совокупности.
Для того чтобы правильно был подобран теоретический закон распределения, необходимо иметь большой статистический материал (порядка нескольких сотен опытов). На практике не всегда можно иметь такой материал и приходится ограничиваться несколькими десятками опытов. На основе этого ограниченного по объему материала можно хотя бы ориентировочно определить характеристики случайной величины Х.
Оценить
некоторый параметр
генеральной совокупности (математическое
ожидание, дисперсию, среднее квадратическое
отклонение и т.д.) случайной величины
Х это
значит найти его приближенное значение
по данным
наблюдения и определить вероятность
того, что
отклонится от
не более чем
на
.
Пусть исследуется некоторая случайная величина Х. Требуется найти оценку для параметра случайной величины по результатам n независимых наблюдений. Что бы оценка была «доброкачественной» к ней предъявляется ряд требований: она должна быть состоятельной, несмещенной и эффективной.
Оценка
называется состоятельной,
если при увеличении числа опытов n
она сходится
по вероятности к параметру
:
.
Т.е., если по мере роста
числа наблюдений n
(при
в случае конечной генеральной совокупности
объема N и при
в случае бесконечной генеральной
совокупности) эта оценка стремится к
оцениваемому параметру
.
Свойство состоятельности обязательно для любого правила оценивания (не состоятельные оценки не используются)
Оценка называется несмещенной, если ее математическое ожида-
ние
равно
:
.
Требование
несмещенности особенно важно при малом
количестве наблюдений. Так из двух
оценок дисперсии
и
обе оценки состоятельны, но только
вторая из них является несмещенной,
т.к. первая содержит систематическую
отрицательную погрешность
,
которая с ростом n
убывает.
Оценка
называется эффективной,
если она по сравнению с другими оценками
имеет наименьшую дисперсию:
.
Так
если имеется выборка из нормально
распределенной генеральной совокупности
,
,
…,
,
то среднее (математическое ожидание)
можно оценить двумя способами:
;
.
Обе эти оценки будут
близки, они обе обладают свойствами
состоятельности и несмещенности, однако
можно показать, что дисперсия при первом
способе оценки равна
,
а при втором равна
,
что существенно больше, чем
.
И здесь первый способ оценки теоретического
среднего является состоятельным,
несмещенным и эффективным, а второй –
только состоятельным и несмещенным.