1.3.7. Упрощение вычисления выборочного коэффициента корреляции.

Процедура вычисления выборочного коэффициента корреляции довольно громоздкая, в вычислительном плане, процедура. Ее можно значительно упростить, если перейти к условным вариантам:

, ,

где и ложные нули. В этом случае вычисляется по формуле

.

Повторим здесь вычисления (для корреляционной таблицы 15), пользуясь понятием ложного нуля и условных вариант. Перейдем к условным вариантам. (в качестве ложного нуля взята варианта , имеющая наибольшую частоту , шаг - разность между двумя соседними вариантами), .

Составим теперь корреляционную таблицу 18 в условных вариантах.

Таблица 18.

U V	-2	-1	0	1	2
-2	10	8	-	-	-	18
-1	-	12	7	-	-	19
0	-	-	28	6	-	34
1	-	-	-	8	9	17
2	-	-	-	-	12	12
	10	20	35	14	21

Если значения и равноотстоящие и возможно дробные, то и - целые малые числа. Выигрыш в вычислительной работе будет наибольшим, когда именно и - дробные.

Теперь

.

Найдем вспомогательные величины.

,

.

Теперь.

,

.

Следовательно

.

1.3.8. Выборочное корреляционное отношение

Для оценки тесноты линейной корреляционной связи между признаками в выборке служит выборочный коэффициент корреляции . Если же корреляционная связь не является линейной, то для оценки тесноты такой корреляционной связи вводятся другие характеристики:

- выборочное корреляционное отношение Y к X;

- выборочное корреляционное отношение Х к Y.

Выборочным корреляционным отношением Y к X называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:

,

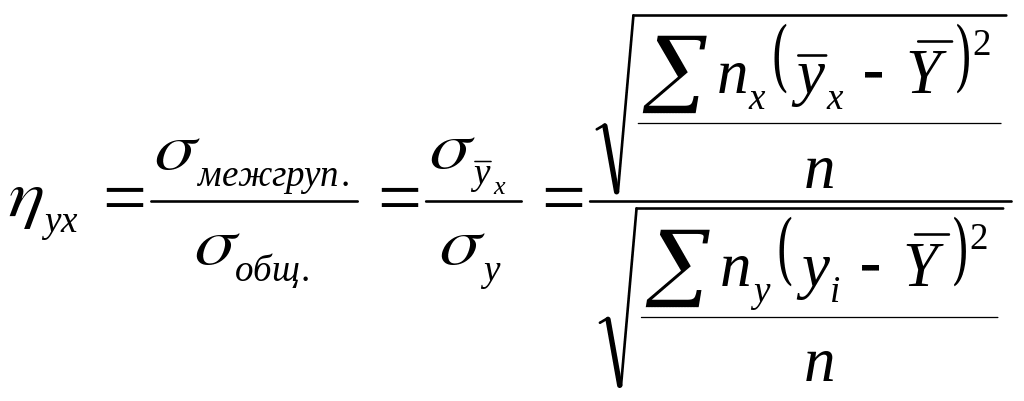где n – объем выборки (сумма всех частот), - частота значения х признака Х, - частота значения y признака Y, - общая средняя признака Y, - условная средняя признака Y.

Выборочное корреляционное отношение Х к Y определяется аналогично:

.

Путь отыскания рассмотрим на примере.

Пусть дана корреляционная таблица 19 признаков Х и Y.

Таблица 19.

Х Y	10	20	30
15	4	28	6	38
25	6	-	6	12
	10	28	12

Р е ш е н и е.

Общая средняя: .

Среднее квадратическое отклонение:

.

Межгрупповое среднее квадратическое отклонение:

Теперь искомое корреляционное отношение .

Выборочные корреляционные отношения и обладают одинаковыми свойствами выборочного корреляционного отношения .

Основные свойства выборочного корреляционного отношения .

1. .

2. Если , то признак Y с признаком Х корреляционной зависимостью не связан.

3. Если , то признак Y связан с Х функциональной зависимостью.

4. Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции, т.е. .

5. Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место точная линейная корреляционная зависимость. Т.е., если , то точки , , …, лежат на прямой регрессии, найденной способом наименьших квадратов.

Из приведенных свойств для видно, что с возрастанием корреляционная связь между признаками Y и Х становится более тесной и т.о. служит мерой тесноты корреляционной связи между признаками Y и Х любой формы (в том числе и линейной). В этом состоит преимущество корреляционного отношения перед коэффициентом корреляции , который оценивает тесноту лишь линейной зависимости. Вместе с тем, корреляционное отношение обладает недостатком: оно не позволяет судить, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т.д., что объясняется тем, что при определении корреляционного отношения форма связи во внимание не принималась.

П р и м е р.

Найдем значение для рассмотренной ранее задачи (таблица 20).

Таблица 20.

Х Y	1	2	3	4	5
14	10	8	-	-	-	18
15	-	12	7	-	-	19
16	-	-	28	6	-	34
17	-	-	-	8	9	17
18	-	-	-	-	12	12
	10	20	35	14	21
	14	14,6	15,8	16,57	17,57

, , , , ,

, .

.

Следовательно, . Поскольку близко к единице, то Y связано с Х почти функциональной зависимостью (т.е. Y связано с Х тесной корреляционной связью). Поскольку , то связь линейная.