Свойства коэффициента корреляции

Выборочный коэффициент корреляции имеет важное самостоятельное значение и обладает следующими свойствами.

1. Абсолютная величина выборочного коэффициента корреляции не превосходит единицы, т.е. .

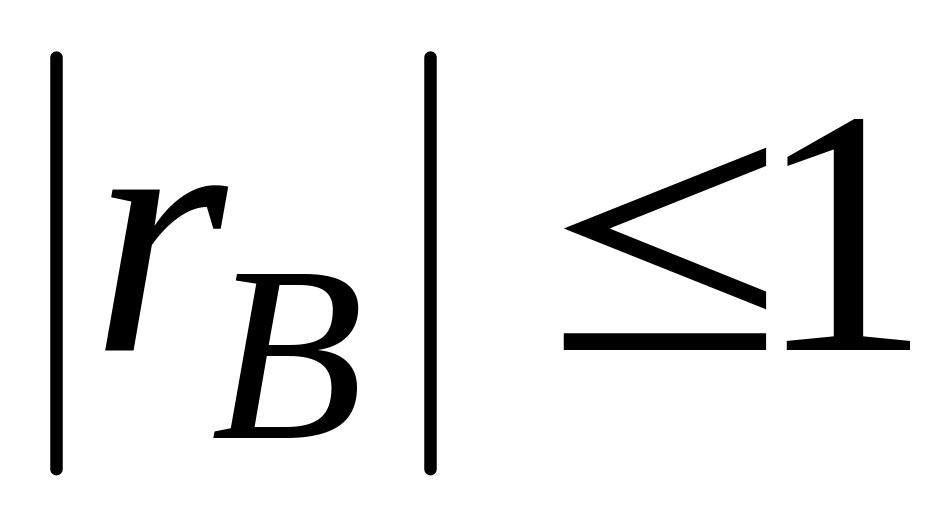2. Если 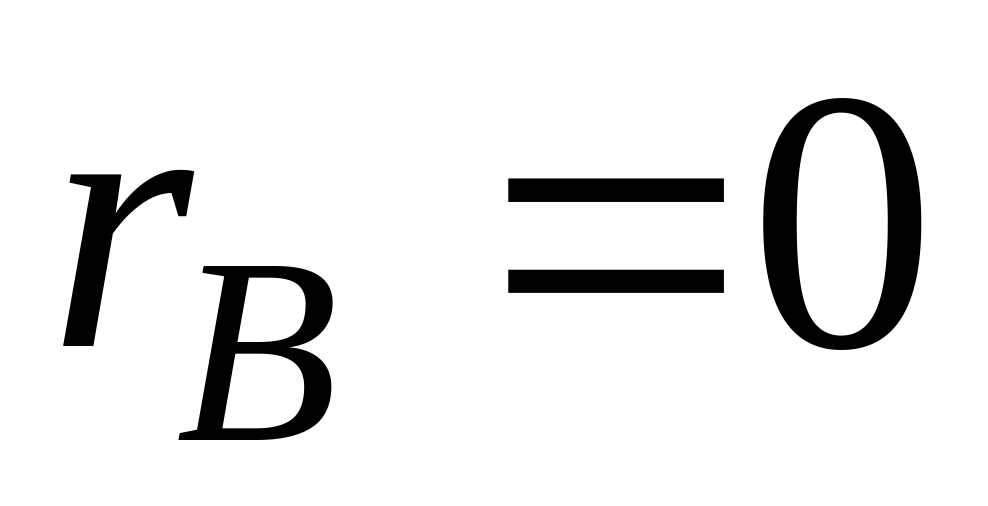и выборочные линии регрессии – прямые, то Х и Y не связаны линейной корреляционной зависимостью. В этом случае признаки Х и Y могут быть связаны или нелинейной корреляцией или даже функциональной зависимостью.

3. Если абсолютная величина 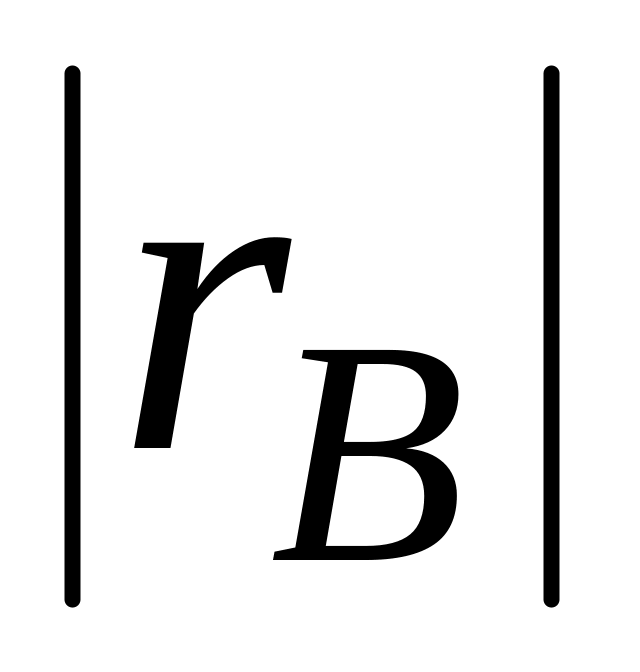равна единице, то наблюдаемые значения признаков связаны линейной функциональной зависимостью.

4. С возрастанием абсолютной величины линейная корреляционная зависимость становится более тесной и при 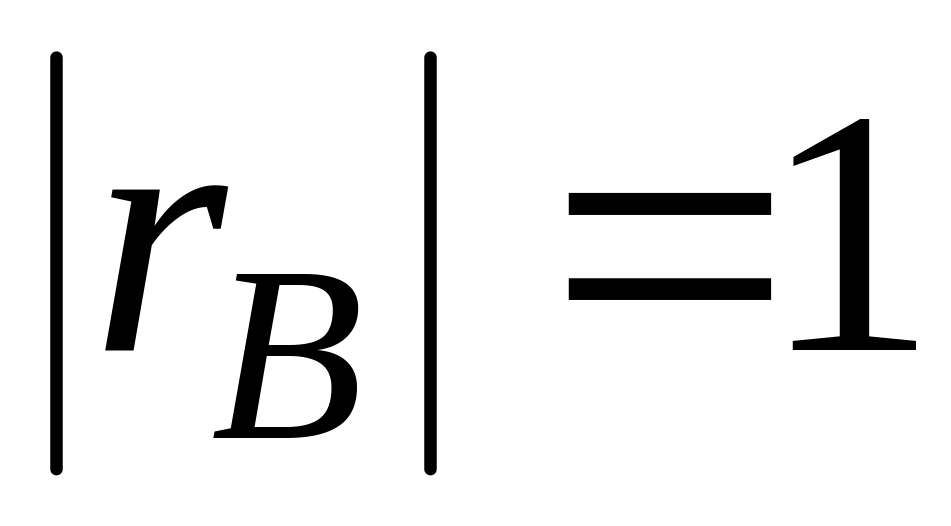переходит в функциональную зависимость.

Таким образом, выборочный коэффициент корреляции характеризует тесноту линейной связи между количественными признаками в выборке: чем ближе он к единице, тем связь сильнее, чем ближе к нулю, тем связь слабее.

П р и м е р

Найдем уравнения прямых (прямой и обратной) регрессии по сгруппированным данным приведенной корреляционной таблицы 15.

Будем оперировать формулами:

, ,

.

.

.

.

,

,

.

,

.

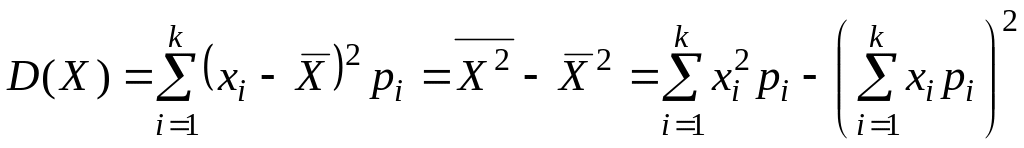Следовательно

.

Отмечаем, что коэффициент корреляции здесь близок к единице, что говорит в пользу тесной линейной корреляционной связи между величинами Х и Y. Теперь уравнение прямой линии для прямой регрессии имеет вид

( ): или

Уравнение для прямой линии обратной регрессии имеет вид

( ): или .

Найдем угол между прямыми и . Разрешим уравнение относительно y.

.

Теперь . Малость угла между прямыми и так же говорит о сильной связи Х и Y.

Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между признаками Х и Y, полученное по данным выборки, может быть распространено и на генеральную совокупность. Для оценки коэффициента корреляции нормально распределенной генеральной совокупности (при ) можно воспользоваться формулой

.

В нашем случае ряд распределения СВ X (Таблица 16)

Таблица 16.

Х	1	2	3	4	5
	10	20	35	14	21
	0,1	0,2	0,35	0,14	0,21

дает , , .

Ряд распределения СВ Y (Таблица 17)

Таблица 17.

Y	14	15	16	17	18
	18	19	34	17	12
	0,18	0,19	0,16	0,17	0,12

дает , , .

Критические границы отношения по таблице приложения 2 с вероятностью нулевой ошибки , , . Т.е. в этом случае воспринимаем совокупность случайных величин Х и Y как единую двумерную нормально распределенную случайную величину.

,

.