Парная корреляция Статистическое оценивание парной корреляции и регрессии

Если переменные х и y представляют двумерную нормально распределенную случайную величину, то существует две регрессии (две прямые регрессии). Одна определяет зависимость y от х, другая - х от y.

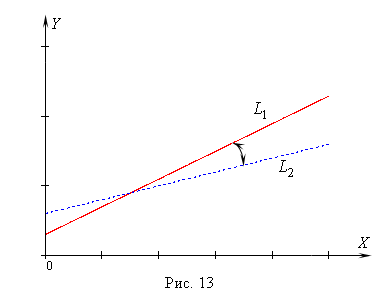
Условно модель называют прямой регрессией, а модель - обратной регрессией. В общем случае и - разные прямые. Они пересекаются в центре тяжести и образуют «ножницы» (Рис. 13). Чем уже «ножницы», тем ближе стохастическая связь к функциональной. При функциональной же связи обе прямые сливаются. Таким образом, уравнение не является алгебраическим, т.е. из него нельзя получить х как функцию y, т.к. эта модель полу-

чена путем минимизации суммы квадратов отклонений вдоль оси ОХ. Т.е., при построении прямых линий прямой и обратной регрессии минимизируются разные величины.

Формулы для вычисления коэффициентов и в случае прямой регрессии имеют вид:

;

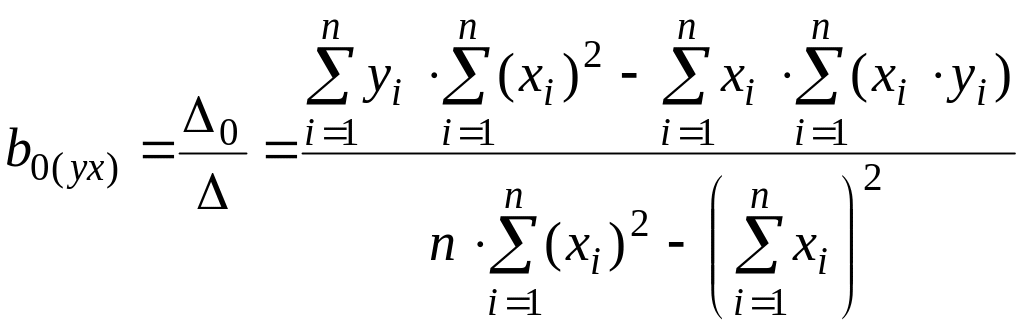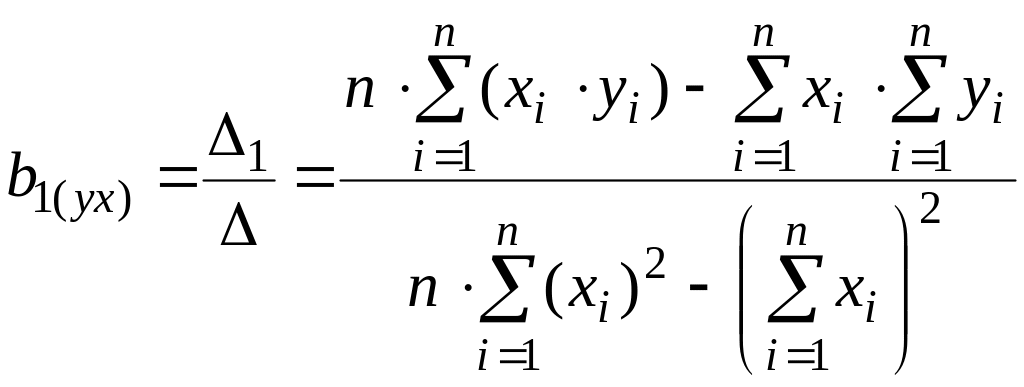. (7)

При обратной регрессии коэффициенты вычисляются по формулам:

;

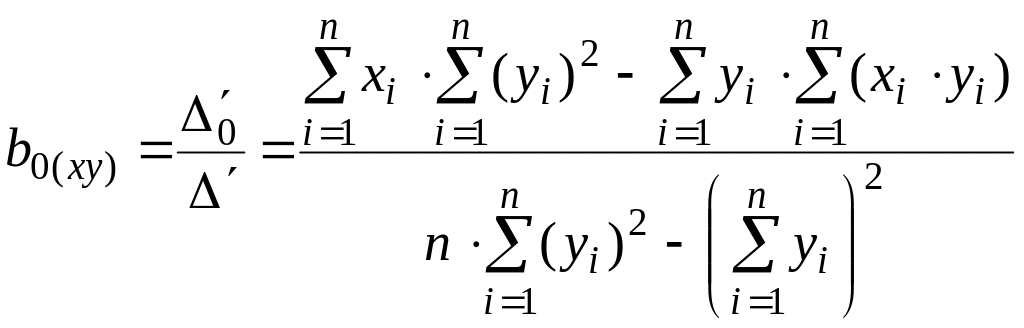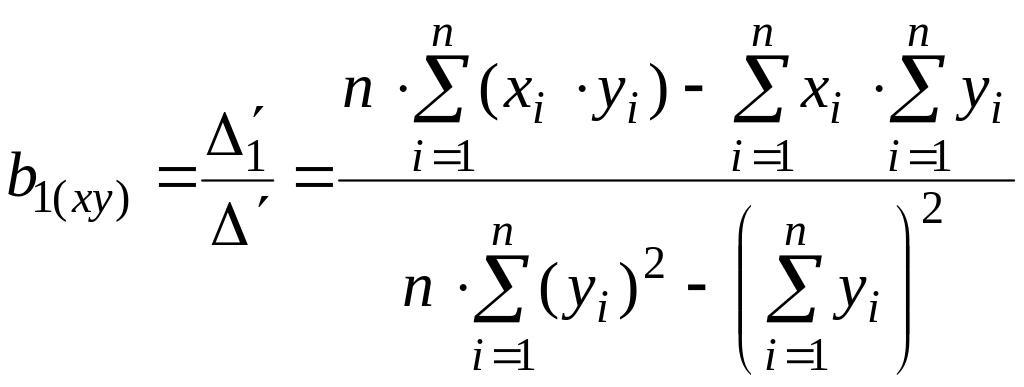. (8)

1.3.4. Корреляционная таблица

При большом числе наблюдений одно и то же значение х может встретиться раз, одно и то же значение y - раз, одна и та же пара чисел может наблюдаться раз. Данные наблюдений группируются и записываются в таблицу, которая называется корреляционной.

Рассмотрим последующие выкладки на примере.

П р и м е р

На 100 участках земли площадью 0,3 га каждый с разным количеством x (т.) внесенных удобрений произведено обследование урожайности y (ц.). Результаты обследования представлены (сгруппированы) в таблице.

Таблица

Х Y	1	2	3	4	5
14	10	8	-	-	-	18
15	-	12	7	-	-	19
16	-	-	28	6	-	34
17	-	-	-	8	9	17
18	-	-	-	-	12	12
	10	20	35	14	21

Здесь на пересечении строк и столбцов вписаны частоты наблюдаемых пар значений признаков. Например, частота 12 указывает, что пара чисел наблюдалась в эксперименте 12 раз. означает, что значение признака , в сочетании с различными значениями признака Y, наблюдалось 20 раз, а - значение , в сочетании с различными значениями Х, наблюдалось 34 раза.

Построение прямых линий регрессии по сгруппированным данным

Для определения параметров уравнения прямой регрессии y на х имеем систему уравнений (7). Здесь предполагалось, что значение х и соответствующие им значения у наблюдались по одному разу. Теперь запишем систему (7) так, чтобы она отражала данные корреляционной таблицы. Воспользуемся тождествами:

(т.к. ), ,

(т.к. ),

(учтено, что пара чисел наблюдалась раз).

Тогда из системы (7) имеем:

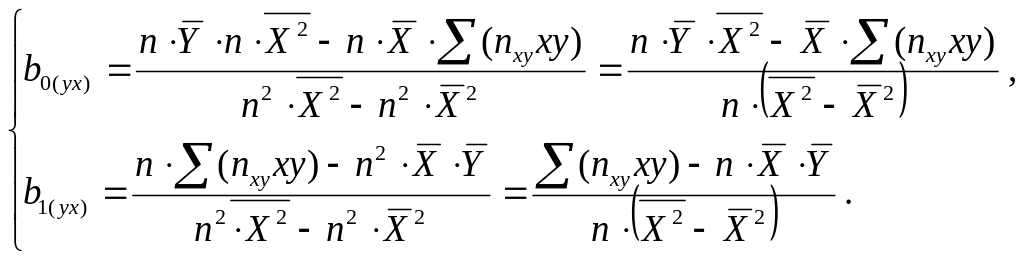
Поскольку же , то .

Если умножить теперь обе части последнего равенства на дробь , то получим .

Обозначим в последнем соотношении правую часть через - выборочный коэффициент корреляции. Теперь или .

Теперь, используя понятие коэффициента корреляции, легко запишутся уравнения прямых линий, как прямой регрессии:

,

так и обратной регрессии:

.