Методы построения, преобразования и оценки парных зависимостей по экспериментальным данным
Пусть
имеется n
пар наблюдений значений функции
,
полученных при фиксированных значениях
независимой переменной
(Таблица):
Таблица
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
х |
1,5 |
4,0 |
5,0 |
7,0 |
8,5 |
10,0 |
11,0 |
12,5 |
y |
5,0 |
4,5 |
7,0 |
6,5 |
9,5 |
9,0 |
11,0 |
9,0 |
Расположение точек на плоскости в прямоугольной системе координат приведено на рис. 11. Представленная система точек часто получается в эксперименте, когда значение аргумента (фактора) мы фиксируем сами.
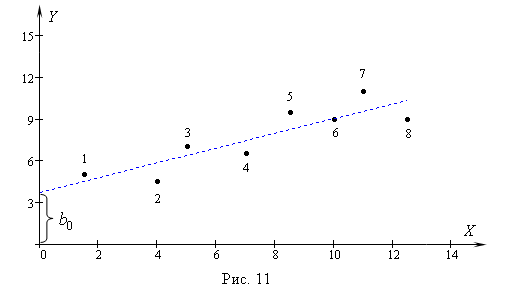
Задача
линейного
регрессионного анализа состоит в том,
чтобы, зная положение точек на плоскости,
так провести прямую линию (линию
регрессии), чтобы сумма квадратов
отклонений
вдоль оси OY
этих точек от проведенной прямой была
наименьшей.
Будем
считать, что рассматриваемая линия –
прямая линия с уравнением
.
В этом случае
сумма квадратов отклонений:
.
-
функция двух переменных, которая
достигает минимума (экстремума) в точках,
в которых частные производные по
переменным
и
обращаются в ноль:
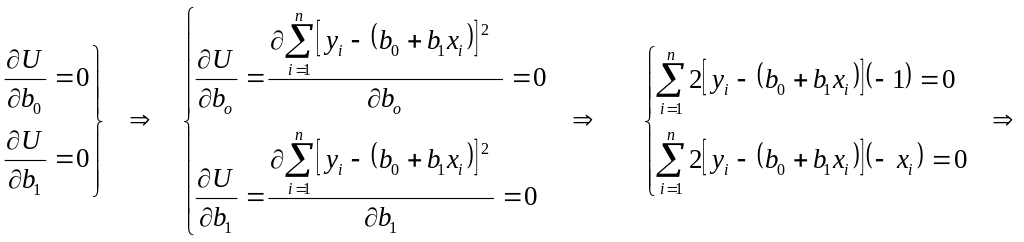
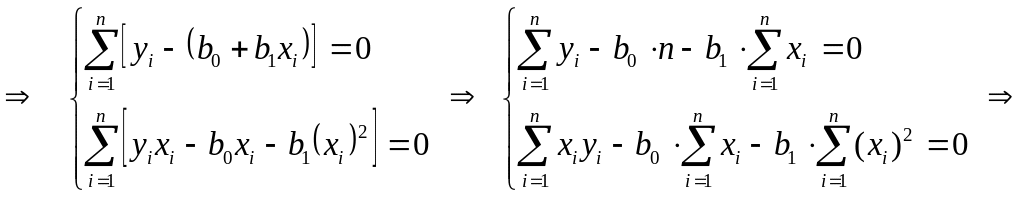
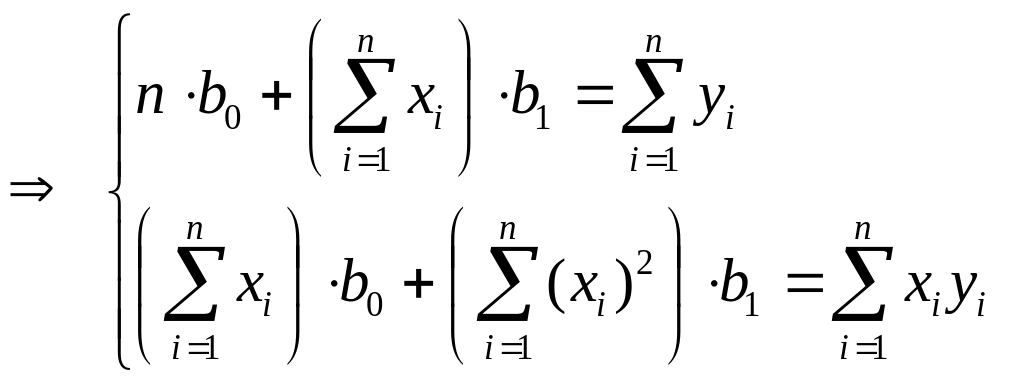(6)
Решая систему (6) методом Крамера, получаем
;
;
.
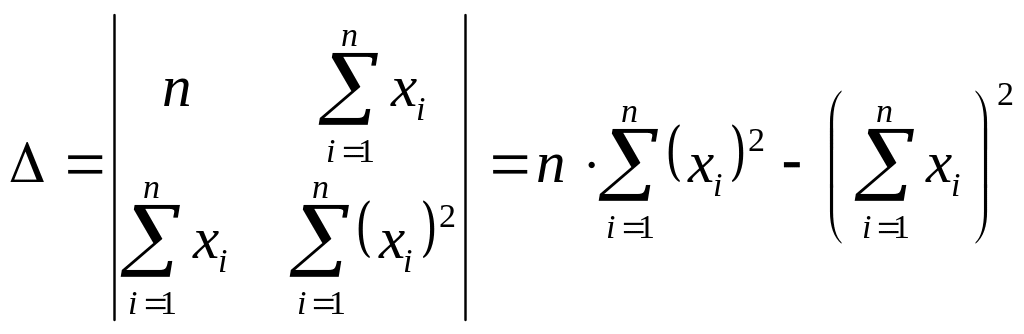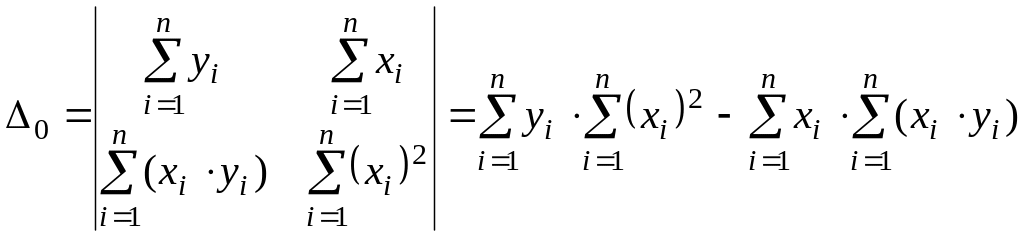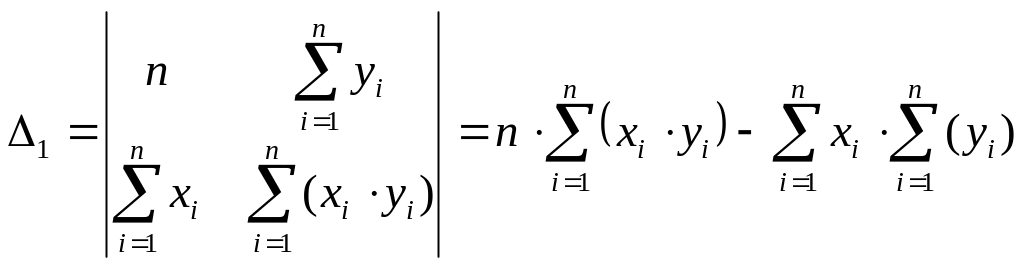Следовательно
;
.
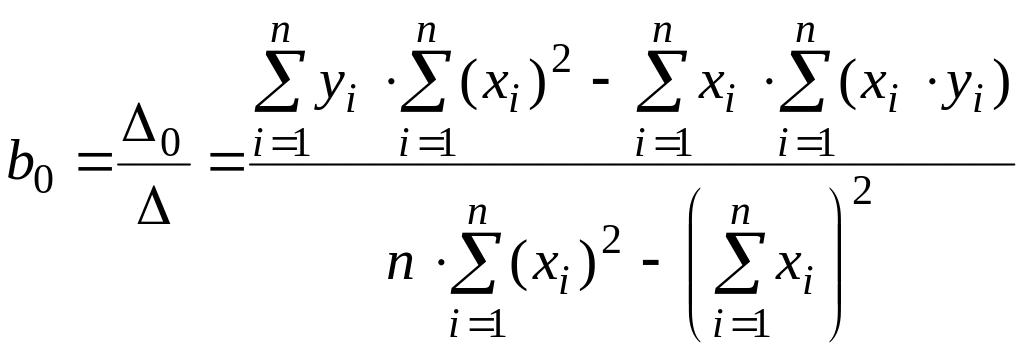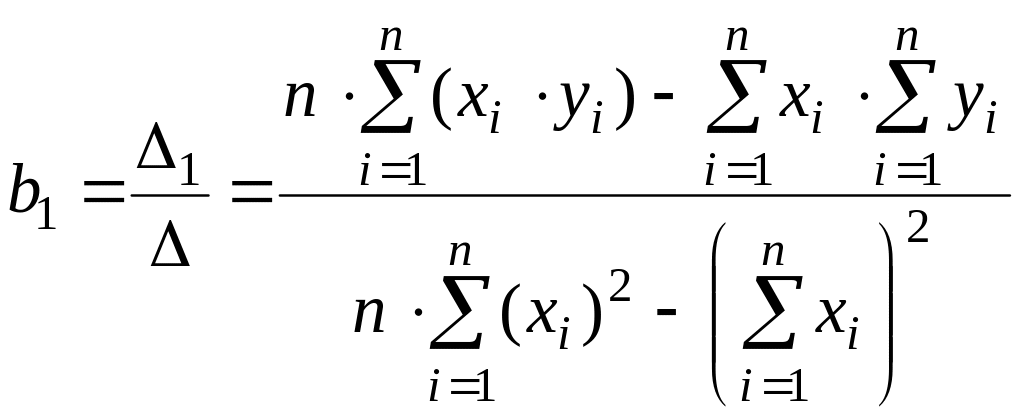Для построения линии регрессии по приведенным числовым данным сведем расчетные данные в следующую таблицу.
Таблица
-
№ п/п
1
1,5
5,0
2,25
7,50
2
4,0
4,5
16,0
18,00
3
5,0
7,0
25,0
35,00
4
7,0
6,5
49,0
45,50
5
8,5
9,5
72,25
80,75
6
10,0
9,0
100,0
90,00
7
11,0
11,0
121,0
121,00
8
12,5
9,0
156,25
112,50
59,5
61,5
541,75
510,25
Теперь:
,
.
Следовательно,
уравнение регрессии, т.е. формула, которая
отображает с некоторой вероятностью
зависимость y
от х,
построенная по экспериментальным
точкам, имеет вид
.
Различают два вида связи: функциональную и стохастическую. Линейная функциональная связь, в данной задаче, имела бы место, если бы все точки эксперимента располагались на прямой регрессии. При наличии же погрешностей измерения связь между х и y является стохастической (вероятностной). В случае стохастической связи функцию y называют функцией отклика, зависимой переменной, предикатом, а независимую переменную х - входной переменной, фактором, регрессором.
Л-7