Курс «Математическая статистика»
ПМИН-III (февраль-май 2013)
Л-1
Законы теории вероятности представляют собой закономерности, существующие в массовых случайных явлениях. Предполагается, что вероятность Р случайного события А или закон распределения случайной величины известны. На практике с таким положением встречаются редко. Все необходимые характеристики случайного события или случайной величины находятся из специально поставленных опытов или из систематических наблюдений за течением явления.
Предмет математической статистики состоит в разработке методов регистрации, описания и анализа опытных данных, полученных в результате изучения массовых случайных явлений.
Типичными задачами математической статистики являются:
- нахождение неизвестной вероятности Р случайного события А на основании наблюдений;
- определение вида закона распределения случайной величины Х на основании физической сущности Х или опыта. То есть определяется, подчиняется ли Х
закону
Бернулли -
,
закону
Гаусса -
,
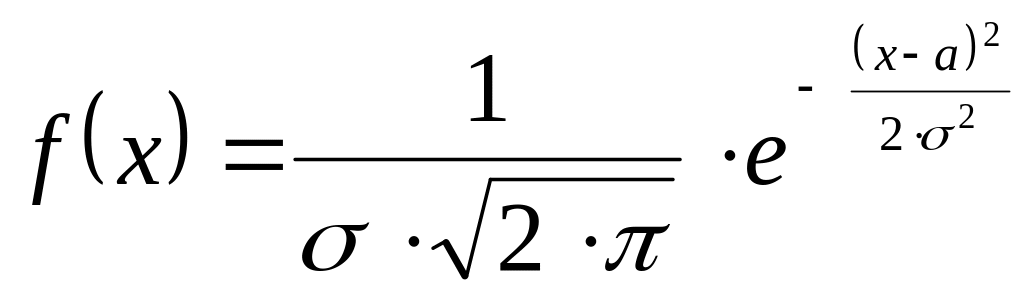закону
Коши -
или какому-либо другому закону;
-
нахождение неизвестных параметров
принятого закона распределения (например,
а и
);
- проверка правдоподобия гипотез, то есть того насколько принятый закон вероятен.
Генеральная и выборочная совокупности
Генеральной совокупностью называется масса всех N изучаемых объектов.
Выборкой называется совокупность n случайно отобранных объектов из изучаемых N объектов.
Объемом генеральной совокупности или выборки называется число объектов этих совокупностей. Например, N=1000, n=100.
Выборка называется повторной или бесповторной в зависимости от того возвращается или не возвращается отобранный объект перед отбором следующего в генеральную совокупность. Обычно пользуются бесповторным случайным отбором. Всегда выборка должна быть случайной.
Статистический ряд
Пусть
произведено
наблюдений случайной величины Х
(отклонение
длины детали от проектной) и получен
ряд значений, записанных в порядке
наблюдений:
.
Написанный
ряд – простая
статистическая совокупность,
являющаяся первичным статистическим
материалом, который подлежит обработке
и анализу. Наблюдаемое в i-том
опыте значение
называется вариантой
случайной
величины Х.
Простая статистическая совокупность
подвергается обработке. Строится
статистический
ряд.
Статистическим
рядом случайной
величины Х
называется
совокупность ее значений
, записанных в порядке возрастания их
численных значений, и их частостей
или частот
.
Для рассмотренного примера статистический ряд имеет вид
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
3 |
4 |
3 |
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Здесь
n=20
– количество
испытаний,
- частость значения случайной величины
,
- частота (статистическая вероятность).
Очевидно
и
.
При
большом числе наблюдений n
(выборке
большого объема) и большом числе k
различных
значений
статистический ряд становится громоздким
и мало удобным для исследования. В этом
случае строится
интервальный статистический ряд.
Для чего размах статистического ряда
делится на 10-20 интервалов (разрядов).
Подсчитывается число значений
величины Х,
приходящихся на каждый i-тый
интервал. Статистическая вероятность
(частота) попадания величины Х
в i-тый
интервал равна
.
Интервальный статистический ряд будет:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В
свою очередь интервальный статистический
ряд можно преобразовать в точечный,
если каждый интервал
заменить его серединой
,
тогда точечный
статистический ряд
будет:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
