МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ДВНЗ «КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

ІМЕНІ ВАДИМА ГЕТЬМАНА»

Факультет інформаційних систем і технологій

Кафедра інформатики

Звіт

з лабораторної роботи

З дисципліни “Економічна кібернетика”

Тема:

Дослідження моделей хаотичних систем

Модель Ресселера

Виконав: Авесідіс Іоанніс,

Студент 3-го курсу

групи ЕК-02

Перевірив: викладач

Овчаренко Андрій Анатолійович

Київ – 2013

Стислі теоретичні відомості:

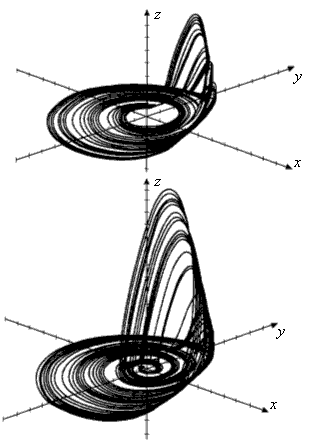
Дивний аттрактор в моделі Ресслера

     Розглянемо модель хаотичного поведінки, запропоновану О.Ресслером:

(1)

де а , b , з - позитивні постійні.       Система (1) описує динаміку абстрактної хімічної реакції. Вона має дві нерухомі точки :

Надалі будемо розглядати явища, що відбуваються тільки в околиці першої нерухомої точки, яку позначимо Р ₀ . 

     Лінійний аналіз стійкості точки Р ₀ показує, що в широкому діапазоні значень параметрів моделі а , b , з вона нестійка . У її околиці поведінку системи має такі особливості: траєкторії відштовхуються від Р ₀ вздовж двовимірної поверхні в фазовому просторі, на якій нерухома точка виглядає як нестійкий фокус , і притягаються вздовж одновимірної кривої (такий тип нерухомої точки відповідає сідла-фокусу в тривимірному фазовому просторі). Дана конфігурація призводить до нестійкості - основний особливості хаотичного руху. Одночасно не виключається і повернення нестійких траєкторій в околицю точки Р ₀ , що в результаті і обумовлює формування дивного аттрактора . 
     Дивні атрактори, що виникають в системі (4.15) при b = 0,3, з = 4,5 і різних значеннях параметра а показані на малюнку. При а = 0,32 (малюнок угорі ) усі траєкторії повертаються до Р ₀ з одного боку площини ХZ , однак при збільшенні а до 0,38 ( малюнок унизу ) з'являються траєкторії, що повертаються і з іншого боку. Ці два види руху зазвичай називаються спіральним і гвинтовим типами хаосу, відповідно.

Дисипати́вна систе́ма (або дисипати́вна структу́ра) — відкрита нелінійна система, яка є далекою від стану термодинамічної рівноваги. Така система є нерівноважною завдяки розсіянню енергії, одержуваної ззовні. Внаслідок самоорганізації у таких системах можуть виникати стійкі структури, які існують за умови постійної дисипації, тобто втрати системою енергії. З появою складної впорядкованої структури в системі зростає ентропія, яка компенсується негативним потоком ентропії зовні.

Консервативна система (від  conservo - Зберігаю) - фізична система, робота неконсервативних сил якої дорівнює нулю і для якої має місце закон збереження механічної енергії, тобто сума кінетичної енергії і потенційної енергії системи постійна

Дивергенція векторного поля

Розглянемо деяку точку P векторного поля A(P) і оточимо її замкнутою поверхнею S, що повністю знаходиться у полі. Обчислимо потік вектора через поверхню S і візьмемо відношення цього потоку до об’єму V області Ω, обмеженою поверхнею S:

An(P) – проекція векторного поля на нормаль n до поверхні S в будь-якій її точці

В полі швидкостей рідини це відношення визначає кількість рідини, що виникає за одиницю часу в області Ω, віднесене до одиниці об’єму, тобто середню об’ємну потужність джерела, а якщо потік зсередини поверхні S менше нуля, то говорять про потужність стоку.

Знайдемо тепер границю відношення:

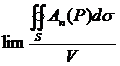
при умові, що область Ω стягується в точку P, тобто V прямує до нуля.

Якщо ця границя додатна, то точка P називається джерелом, а якщо від’ємна, то стоком. сама величина границі характеризує потужність джерела чи стоку.

Дивергенцією (розбіжністю) векторного поля A(P) в точці P називається границя відношення потоку вектора через поверхню, що оточує точку P, до об’єму, обмеженого цією поверхнею, за умови, що вся поверхня стягується в точку P:

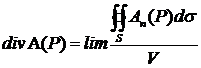
при чому границя обчислюється за умови, що поверхня стягується в точку P.

Дивергенція векторного поля A(P)=Axi+Ayj+Azk виражається формулою:

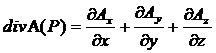
де значення частинних похідних беруться в точці P.

Якщо divA(P)=0, то поле A(P) називається соленоїдальним.

Система рівнянь Лоренца - це тривимірна система нелінійних автономних диференціальних рівнянь першого порядку виду

Ц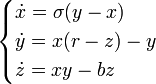 я система виникла в задачі про моделювання конвективного течії рідини, що підігрівається знизу. Таке протягом описується системою диференціальних рівнянь в приватних похідних. Система (1) виходить з неї проектуванням на спеціальне тривимірне підпростір.

при наступних значеннях параметрів: σ = 10, r = 28, b = 8/3. Ця система спочатку була введена як перше нетривіальне галеркінское наближення для задачі про конвекції морської води в плоскому шарі, ніж та мотивувався вибір значень σ, r і b, але вона виникає також і в інших фізичних питаннях і моделях:

• конвекція в замкнутій петлі;

• обертання водяного колеса;

• модель одномодового лазера;

• дисипативний осцилятор з інерційною нелінійністю.

Поведінка рішення системи

При r < 1 система Лоренца (1) має єдину стаціонарну (нерухому) точку — початок координат, до якого притягуються всі траекторії (р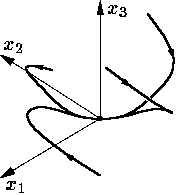ис. 4).

Рис. 4.

При r > 1 початок координат вже нестійкий, бо відповідна матриця ∂ f (x) / ∂ x має одне додатне і два від’ємних власних числа. Крім початку координат при r > 1 існує ще дві стаціонарні точки:

X₁ = ( + (b · (r – 1))^1/2 ; + (b · (r – 1))^1/2; (r – 1)) ; X₂ = ( – (b · (r – 1))^1/2 ; – (b · (r – 1))^1/2; (r – 1)) .

Спочатку всі власні числа λ матриці ∂ f /∂ x у двох нових стаціонарних точках від’ємні (рис. 5).

Рис. 5.

Згодом при зростанні r пара від’ємних власних чисел перетворюється на пару комплексно спряжених чисел з від’ємною дійсною частиною. Кожна з двох траекторії G₁ і G₂ , що "виходять" з початку координат у напрямках власного вектора матриці ∂ f (0) /∂ x з додатним власним числом, і "входили" у стійку стаціонарну точку X₁ чи X₂, починають закручуватися спіраллю навколо цієї стаціонарної точки (р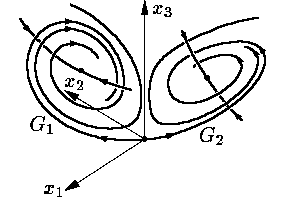ис. 6).

Рис. 6.

При r ≈ 13,92 траекторії Г₁ і Г₂ "входять" у початок координат у напрямку у напрямку власного вектора матриці ∂ f (0) /∂ x з від’ємним власним числом (рис. 7).

Рис. 7.

При подальшому зростанні r в околі ще стійких стаціонарних точок з’являються два нестійкі цикли Ф₁ і Ф₂. Лінійні частини операторів слідування для цих циклів мають по два власних значення, що лежать по різні боки від 1. Інакше кажучи, по одному напряму тракторії притягуються до цих циклів, а по іншому — відштовхуються. При цьому дві траекторії G₁ і G₂ притягуються вже до інших стаціонарних точок, ніж до появи нестійких циклів, і закручуються спіраллю навколо них (рис. 8).

Рис. 8.

При r ≈ 24,06 траекторії G₁ і G₂ потрапляють на многовиди притягування до нестійких циклів Ф₁ і Ф₂.

При r = r₀ = σ(σ + b + 3)/(σ – b – 1) ≈ 24,74 матриця ∂ f (X_j) /∂ x (j = 1, 2) має два комплексно спряжених власних числа на уявній осі. Дійсні частини цих власних чисел зростають при зростанні r. Стаціонарні точки X₁ та X₂ гублять свою стійкість, поглинаючи нестійкі цикли (так звана біфуркація Пуанкаре — Андронова — Хопфа). Вже при r > 13.92 система Лоренца має граничну інваріантну множину, яка при r < r₀ не є стійкою, тобто не притягує траекторії. При r ∈ (r₀; 50] ця множина стає стійкою. Її називають аттрактором Лоренца. На рис. 9 подано двовимірну проекцію траекторії в околі аттрактора Лоренца. Траекторія робить кілька обертів навколо однієї стаціонарної точки, потім — навколо іншої і т.і. Кількість таких послідовних обертів навколо стаціонарної точки настільки суттєво залежить від координат початкової точки, що виникає враження хаотичності руху і, навіть, випадковості такого руху.

Рис. 9.

Аттрактор Лоренца A має такі властивості (обґрунтування цих властивостей полягає у тлумаченні результатів числових розрахунків).

1. A є аттрактором у тому розумінні, що існує відкрита в R³ множина B, при якій A = ∩_t≥0 T_tB. Тут T_t — оператор зсуву вздовж траекторій системи на час t. Інакше кажучи, всі траекторії, що мають початок у B (для системи Лоренца за B можна взяти все R³ без стаціонарних точок), притягуються до A.

2. A містить всюди щільну множину періодичних траекторій, кожна з яких є нестійкою.

3. Для довільної траекторії в A з трьох різних характиристичних показників Ляпунова один дорівнює 0 (для напряму потоку f ), один — від’ємний (вздовж відповідного напряму відбувається притягування траекторій), а ще один — додатний (вздовж відповідного напряму відбувається експотенціалльне "розбігання" траекторій навіть при як завгодно малих відхиленнях початкових значень).

4. Локально аттрактор Лоренца має структуру добутку інтервалу на досконалу канторову множину.