12. Реальный газ.
Идеальный газ – есть некоторая идеализация, где не учитываются собственные объёмы молекул и взаимодействия молекул друг с другом (притяжение и отталкивание). Этой идеализацией можно пользоваться когда газ достаточно разрежен. В реальном газе надо учитывать собственные объёмы молекул и взаимодействия между молекулами.
Учёт собственных объёмов молекул сводится к учёту сил отталкивания между молекулами, поскольку именно силы вотталкивания препятствуют проникновению одной молекулы в объём, занимаемый другой молекулой.
Минимальное расстояние, на которое две молекулы могут подойти друг к другу – есть их диаметр. Поэтому, для молекулы не доступен объём, равный:
Тогда
в расчёте на одну молекулу, недоступен
объём, равный учетверённому объёму
одной молекулы (
).
Значит,
Учёт сил притяжения сводится к тому, что на газ оказывается дополнительное давление:
Следовательно:
Тогда уравнение состояния реального газа для одного моля:
- уравнение
Ван-дер-Ваальса
Поправки
и
,
характеризующие данное вещество, можно
определить из уравнения, записав его
для 2-ч разных состояний.
Уравнение Ван-дер-Ваальса для произвольного количества вещества:
13. Изотермы Ван-дер-Ваальса и их анализ.
Для
исследования поведения реального газа
используются изотермы Ван-дер-Ваальса
– кривые зависимости
от
при заданных
,
определяемые уравнением Ван-дер-Ваальса
для моля газа:
.
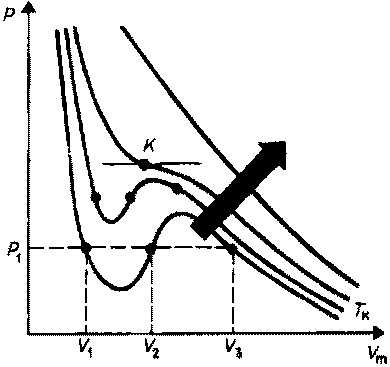
При
изотерма реального газа отличается от
изотермы идеального газа только некоторым
искажением её формы, оставаясь монотонно
спадающей кривой.
При
некоторой температуре
на изотерме имеется лишь одна точка
перегиба
.
Эта изотерма называется критической,
соответствующая ей температура –
критической температурой.
При
изотермы имеют волнообразный характер,
сначала монотонно опускаясь вниз, затем
монотонно поднимаясь вверх и снова
монотонно опускаясь.
Для пояснения характера изотерм, преобразуем уравнение Ван-дер-Ваальса:
Уравнение
третьей степени относительно
может иметь либо три вещественных корня,
либо один вещественный и два мнимых.
Физический смысл имеют лишь вещественные
корни. Поэтому, первому случаю соответствуют
изотермы при низких температурах (
),
т.е. три значения объёма газа
,
,
отвечают одному значению давления.
Второму случаю отвечают изотермы при
высоких температурах.
Рассматривая
различные участки изотермы при
,
видим, что она на участках
и
при уменьшении объёма
давление возрастает, что естественно.
На участке
сжатие приводит к падению давления,
чего не бывает. Наличие этого участка
означает, что при изменении объёма
вещество не может долго оставаться всё
время в виде однородной среды; в некоторый
момент должно наступить скачкообразное
изменение состояния и распад вещества
на две фазы. Таким образом, истинная
изотерма будет иметь вид ломанной линии
.
Часть
отвечает газообразному, а часть
- жидкому состояниям. В состояниях,
соответствующих горизонтальному участку
изотермы
,
наблюдается равновесие жидкой и
газообразной фаз вещества. Вещество в
газообразном состоянии при температуре,
ниже критической, называется паром, а
пар, находящийся в равновесии со своей
жидкостью, называется насыщенным.
Выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами Эндрюса. Отличие экспериментальных данных от теоретических заключается в том, что превращению газа в жидкость в первом случае соответствуют в первом случае горизонтальны участки а во втором – волнообразные.
Для
нахождения критических параметров
подставим их значения в уравнение
:
(1). Поскольку в критической точке все
три корня совпадают и равны, то:
или
(2).
Из того, что уравнения 1 и 2 тождественны,
следует, что в них должны быть равны и
коэффициенты. Поэтому:
,
,
.
Таким образом, критические параметры:
,
,
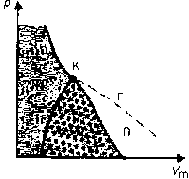
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму на три части.
Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает сжижение. Газ же при температуре выше критической не может быть превращён в жидкость ни при каком давлении.
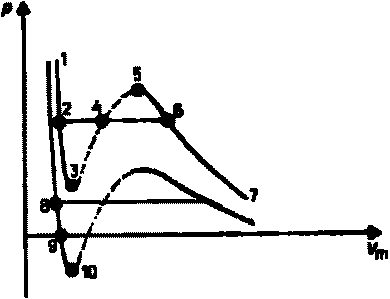
Сравнивая
изотермы Ван-дер-Ваальса и Эндрюса,
видно, что последняя имеет прямолинейный
участок
,
соответствующий двухфазным состояниям
вещества. Правда, при некоторых условиях
могут быть реализованы такие состояния,
изображаемые на кривой Ван-дер-Ваальса
участками
и
.
Эти неустойчивые состояния называют
метастабильными. Участок
изображает перегретую жидкость, а
- перенасыщенный пар.
При
достаточно низких температурах изотерма
пересекает ось
,
переходя в область отрицательных
давлений. Вещество под отрицательным
давлением находится в состоянии
растяжения. При некоторых условиях
такие состояния также реализуются.
Участок
на нижней изотерме соответствует
перегретой жидкости, а участок
- растянутой жидкости.