2 .2. Решение задач о простейших одномерных установившихся течениях вязкой жидкости и их практическое значение.

Одномерное напорное течение между параллельными твердыми неподвижными плоскостями

Постановка задачи.

Между двумя параллельными неподвижными плоскими твердыми стенками течет жидкость под действием постоянного напора. Определить распределение скоростей в потоке и массу жидкости, протекающей через зазор в единицу времени. Принимаем поток плоскопараллельным, ось Oz направляем вдоль нижней плоскости в направлении потока, ось Ox располагаем в плоскости потока. Пусть h - расстояние между плоскостями, – протяженность участка потока.

Сформулируем математическую задачу. Принимаем в соответствии с общей постановкой задачи

,

Подставляем эти выражения в уравнения Навье-Стокса (1.26) и записываем условия прилипания жидкости к твердым границам области течения. Имеем

, (2.13)

(2.14)

Интегрируем уравнение (2.13). Находим

Выполняем граничные условия (2.14), имеем

,

что дает

При этих значениях постоянных получаем

(2.15)

что означает, что распределение скоростей в сечении потока параболическое и симметричное относительно оси потока.

Найдем расход жидкости через сечение потока по формуле

имеем

(2.16)

Эта формула находит большое практическое применение. Прежде всего, имеем качественный результат: расход жидкости через щель пропорционален кубу ее толщины . Это справедливо не только для жидкостей, но и для газов, и подтверждено экспериментом для тонких щелей. Однако, с увеличением толщина щели , справедливость формулы (2.16) нарушается, что может быть связано только с невыполнением принятого нами допущения об одномерности потока. В реальных турбинах, компрессорах, цилиндрах внутреннего сгорания и т.п. стремятся к уменьшению утечек жидкостей и газов из рабочих зон, что достигается уменьшением зазоров в уплотняющих устройствах до таких размеров, при которых формула (2.16) становится справедливой, что позволяет пользоваться этой формулой при расчетах на стадии проектирования соответствующих машин.

Одномерное напорное течение в круглой трубе

Постановка задачи/

В круглой цилиндрической трубе радиуса течет жидкость под действием постоянного напора. Определить распределение скоростей в потоке и массу жидкости, протекающей через сечение трубы в единицу времени.

Для математической формулировки задачи введем в рассмотрение декартову систему координат Oxyz, ось Oz которой направлена по оси цилиндра. Принимаем

Запишем уравнения и граничные условия для такого потока

(2.17)

при (2.18)

Ищем решение задачи (2.17)- (2.18) в таком виде

(2.19)

При этом скорость потока автоматически удовлетворяет граничным условиям (2.18). Постараемся подобрать постоянный множитель А так, чтобы выполнилось тождественно равенство (2.17). Учитываем, что

Уравнение (2.17) приводит к равенству

Следовательно, искомое решение задачи имеет вид

(2.20)

Как видно, эпюра скоростей - параболоид вращения с, осью симметрии,

совпадающей с осью Oz.

Найдем расход жидкости через трубу, пользуясь формулой

Для вычисления интеграла перейдем к полярным координатам. Положим

Имеем

Простые вычисления дают

(2.21)

Это знаменитая формула Гагена-Пуазейля, установленная экспериментально в начале 40-х годов 19 века для трубок малого диаметра Г. Гагеном и Ж. Пуазейлем. С ростом диаметра трубы, или перепада давлений, справедливость формулы (2.21) нарушается. Это означает, что основные допущение, использованное при постановке математической задачи, – допущение об одномерности потока жидкости в трубе и его установившемся характере не всегда соответствует действительности. Как позднее показал Осборн Рейнольдс (конец 19 века), допущение об одномерности потока жидкости в трубе длины L реально выполняется лишь для сравнительно малых чисел параметра

(2.22)

названного числом Рейнольдса ( ).

Опытным путем установлено, что при поток в трубе сохраняется одномерным, жидкость течет слоями - ламинарно. При ламинарный характер течения нарушается, поток становится неодномерным, неустановившимся и неупорядоченным – турбулентным.

Перепад давлений в трубе необходим для преодоления сопротивления, которое стенка трубы оказывает потоку. При установившемся течении силы трения и силы давления образуют уравновешенную систему сил. Силы давления на участке протяженности имеют равнодействующую, равную

Силы трения потока о стенку имеют равнодействующую

Составляем равенство

Отсюда находим силу трения жидкости, приходящуюся на единицу площади стенки трубы.

(2.23)

Коэффициент сопротивления трубы

Для оценки силовых и энергетических потерь на трение в технике используется коэффициент трения, определяемый по формуле

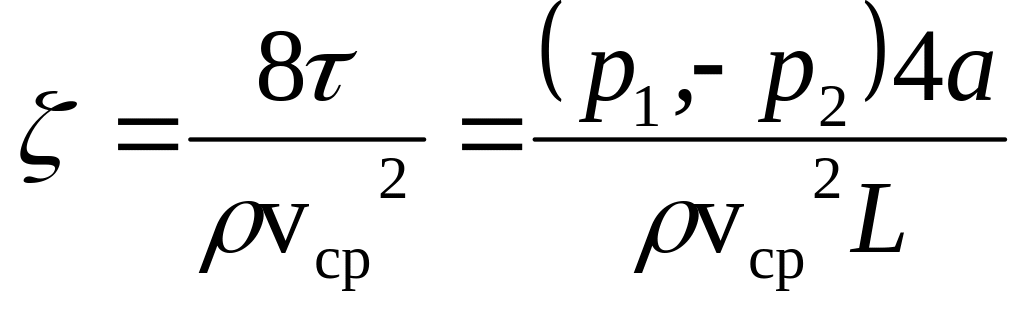(2.24)

Этот коэффициент можно определить теоретически на основе формулы Пуазейля, а также и экспериментально по расходу жидкости через трубу при заданном перепаде давлений.

В случае течения в круглой трубе имеется возможность найти теоретическое значение коэффициента трения, используя формулу (2.21),

согасно которой теоретическое значение скорости равно

При этом откуда следует, что

И поэтому теоретическое значение коэффициента трения для круглой трубы равно

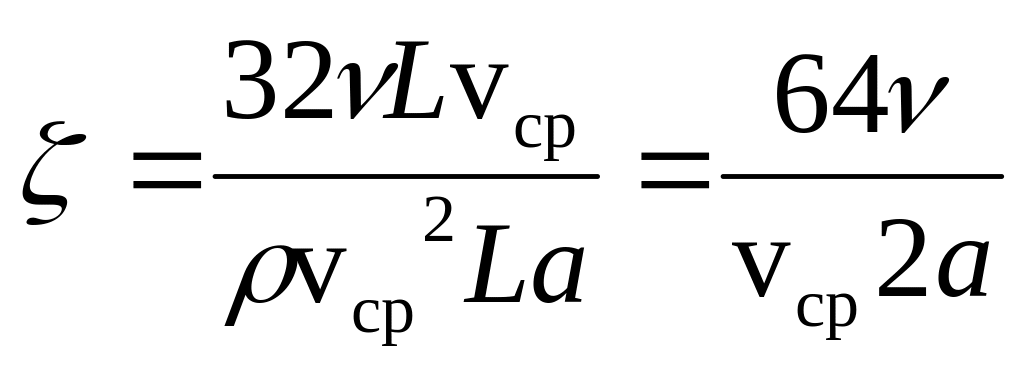
Или

(2.25)

Эта формула экспериментально подтверждается только при . Для диапазона чисел Рейнольдса экспериментально установлена формула Блазиуса

(2.26)

Для диапазона чисел Рейнольдса пригодна экспериментальная формула Никурадзе

(2.27)

Потоки жидкостей (и газов), для которых справедлива формула (), являются слоистыми - ламинарными. Они, как правило, реализуются в тонких каналах – капиллярных трубках. В трубах большого диаметра реализуются не ламинарные потоки, а турбулентные, не обладающие слоистым характером. Распределение скоростей в таких потоках резко отличается от представленного выше. В расчетах используются формулы ().

и гидродинамические модели турбулентных потоков.

Так как трубопроводный транспорт жидкостей и газов широко используется, то высокоточное установление закономерностей потоков этих сред в трубах было и остается одной из центральных задач динамики вязких жидкостей и газов. Неточности формул даже в долях процентов могут приводить к реальным потерям доходов в миллиарды долларов, так как торговля газом и нефтью совершается на сотни миллиардов долларов.

Ламинарные течения реализуются в капиллярных трубках, например, в капиллярах кровеносной системы человека и животных, в технических устройствах типа струйных принтеров и.т.п. Здесь важно отметить, что кровеносные капилляры не являются жесткими и прямолинейными, характер течения в них не является установившимся, а кровь не всегда можно рассматривать как однородную среду. Наука, изучающая механику биологических процессов (биомеханика) сейчас бурно развивается.