1. . Векторно-тензорная форма записи уравнений движения вязких жидкостей и газов

Основные соотношения и допущения для вязкой жидкости и вязкого газа изложены в работе [3]. Это

уравнение неразрывности

(1.1)

уравнение движения в напряжениях (уравнение Коши)

(1.2)

закон сохранения энергии (первый закон термодинамики)

(1.3)

Здесь – тензор напряжений, – тензор скоростей деформаций, плотность, вектор скорости, температура, - тепловая энергия, - коэффициент теплопроводности частицы, – приток тепла к частице в единицу времени (при ), массовая сила, действующая на частицу.

Принимается обобщенная гипотеза Ньютона о линейной зависимости тензора напряжений от тензора скоростей деформаций

(1.4)

где – давление, - единичный тензор - тензор вязких напряжений, имеющий вид

(1.5)

где - коэффициент динамической (сдвиговой) вязкости газа, - коэффициент объемной вязкости газа.

Учитываем, что

, (1.6)

Уравнение баланса энергии (1.3) приобретает вид

(1.7)

2. Уравнения движения вязких жидкостей и газов в декартовых координатах

В проекциях на оси декартовой системы координат x, y, z полная система уравнений, описывающих движение и термодинамику вязкого газа, как нетрудно установить, принимает вид

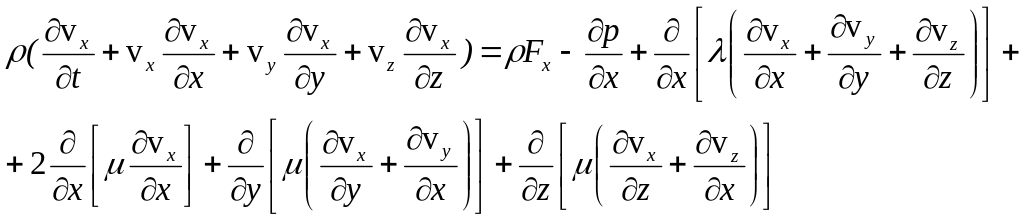
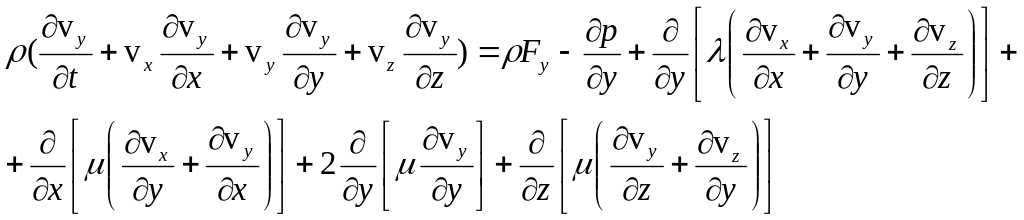(1.8)

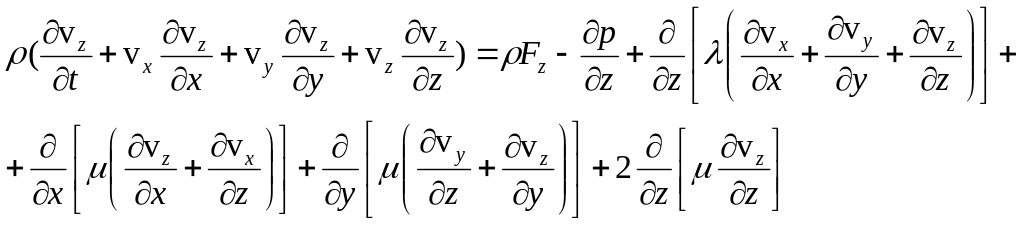
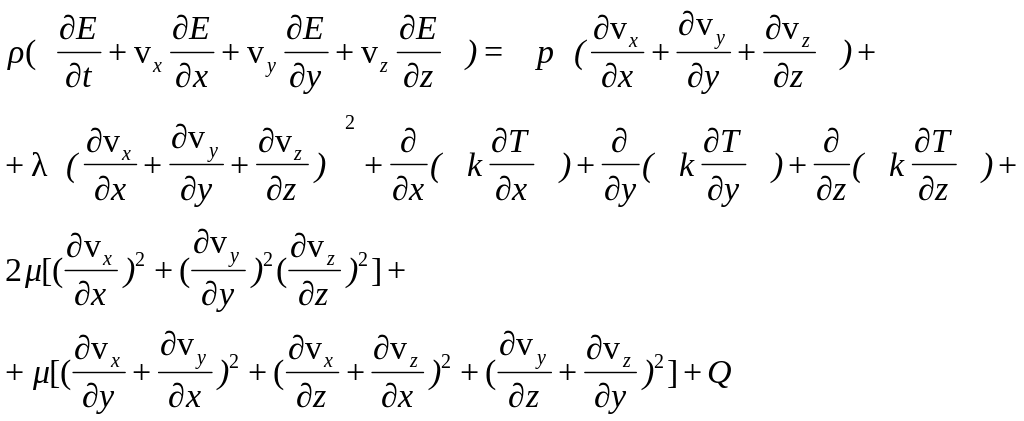
_{В случае вязких газов к записанным уравнениям необходимо добавить алгебраические соотношения состояния:}

, , , , , (1.9)

Здесь - газовая постоянная, и коэффициенты удельных теплоемкостей газа при постоянном давлении и постоянном объеме, соответственно.

Если течение вихревое, то проекции на декартовы оси вектора вихря скорости вычисляются по формулам

, , (1.10)

1.3. Уравнения движения вязкого газа в криволинейных ортогональных координатах

Уравнения движения вязкого газа в криволинейных ортогональных координатах выведены и записаны в книге [7], а метод их вывода кратко изложен также в книге [8]. Ограничимся ниже только записью этих уравнений.

При выборе конкретной криволинейной ортогональной системы координат надо предварительно убедиться в ее ортогональности, записать уравнения связи декартовых координат с криволинейными координатами

, k=1, 2, 3 (1.11)

и следовать предлагаемой ниже последовательности вычислений:

1) определение коэффициентов Ламе по формулам

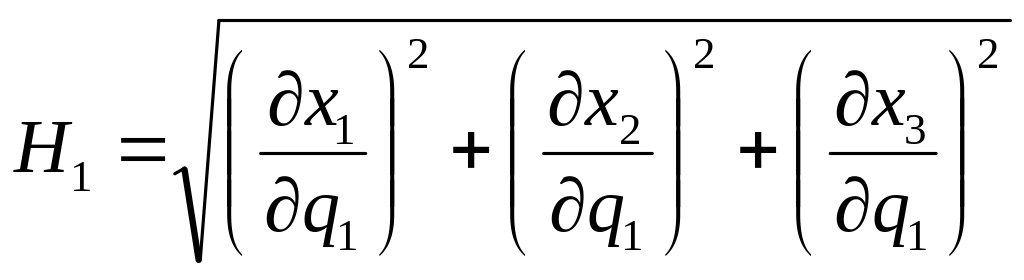
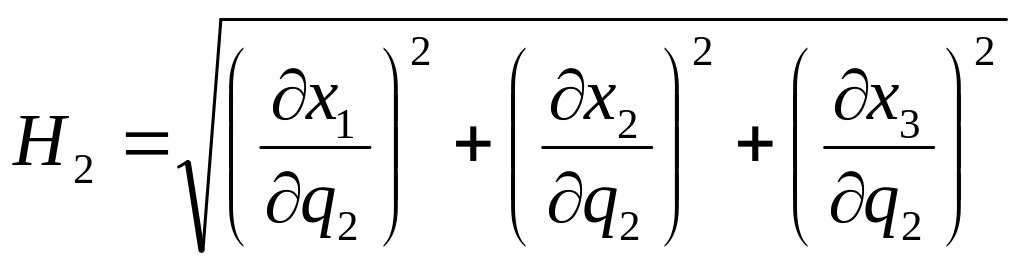(1.12)

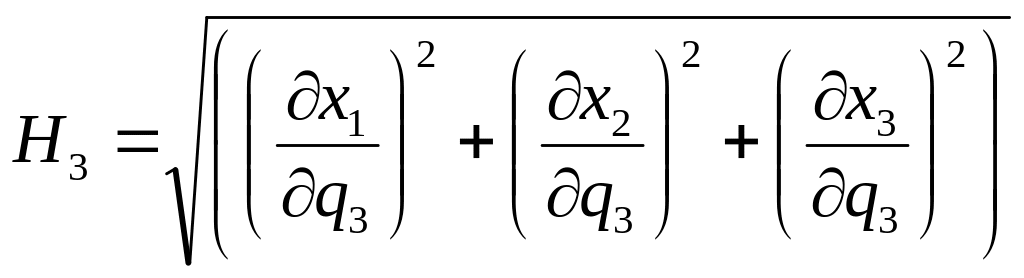
2) определение компонент тензора скоростей деформаций по формулам:

(1.13)

3) определение компонент тензора вязких напряжений

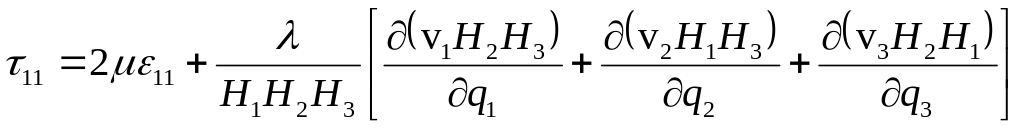
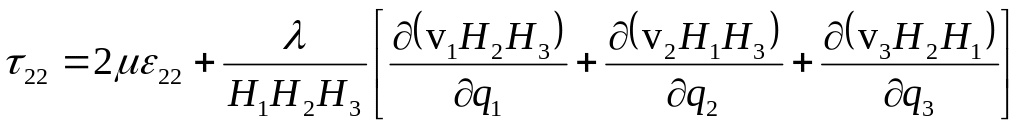_(1.14)

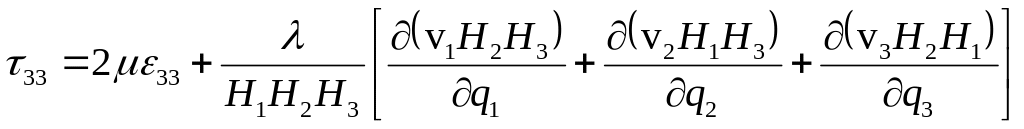
_{4) определение дивергенции вектора скорости}

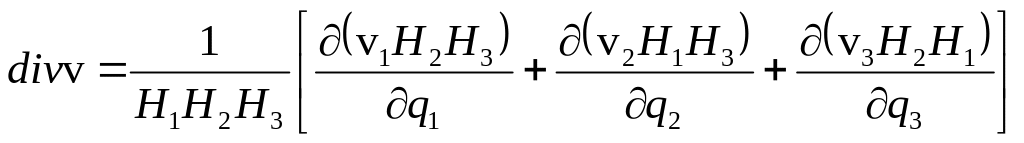(1.15)

5) запись уравнения неразрывности:

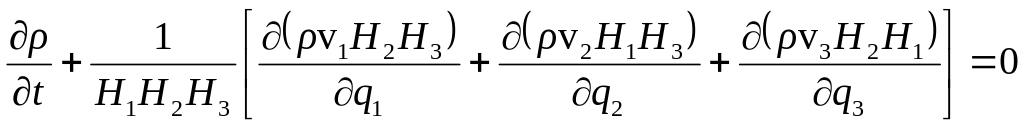, (1.16)

6) запись уравнений движения:

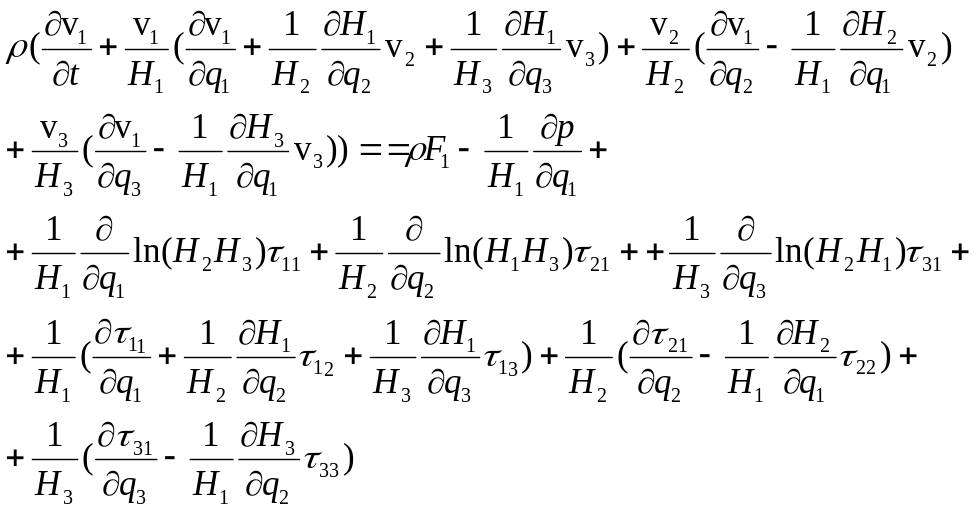
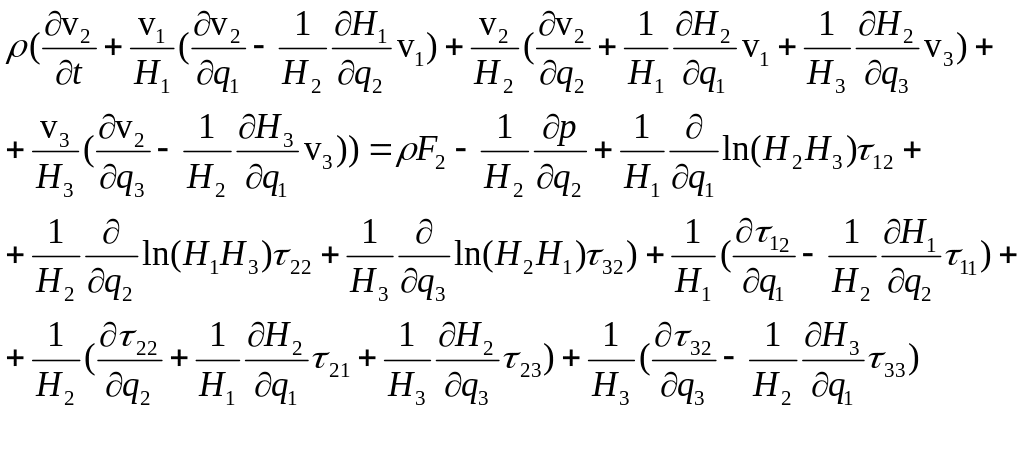
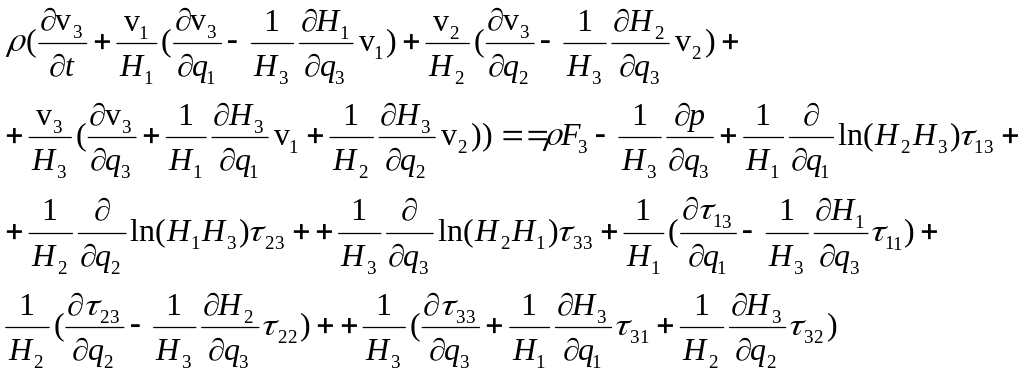
7) запись уравнения баланса энергии

:

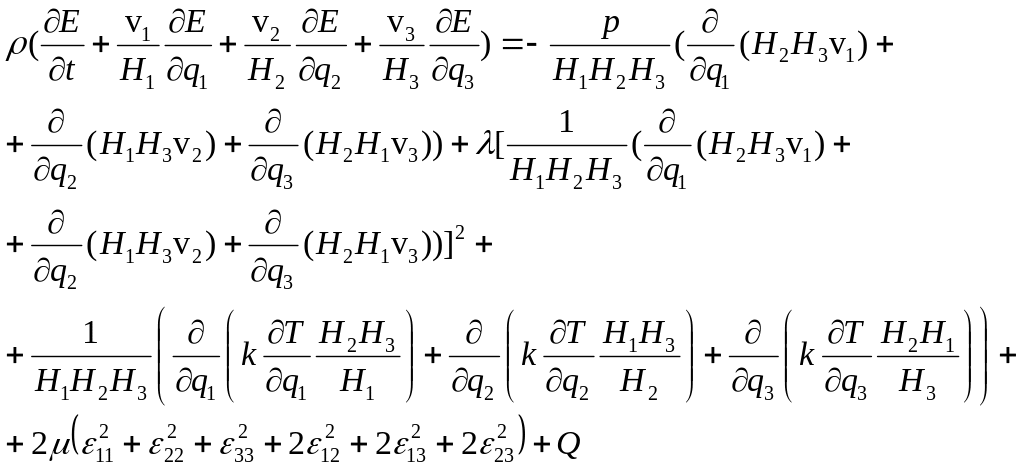
_(1.18)