4.5. Пограничный слой на пластине

Теория пограничного слоя возникла в начале 20 века и находит большое практическое применение в расчете сопротивления и теплообмена при взаимодействии тел с потоками жидкости и газа в энергетике, корабле-, самолето-, ракетостроении и других разделах науки и техники. Основным инструментом для решения соответствующих задач являются численные и аналитико-численные методы в связи с существенной нелинейностью уравнений пограничного слоя.

Рассмотрим в качестве примера простейшую задачу о пограничном слое на полубесконечной твердой пластине нулевой толщины, продольно обтекаемой безграничным потоком вязкой несжимаемой жидкости с постоянной скоростью U на бесконечности, решенную Блпзиусом в 1908 г.)

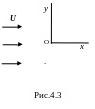Выберем начало координат в передней кромке пластины. В теории пограничного слоя принимается, что в связи с малой толщиной пограничный слой слабо влияет на внешний поток и можно наличием пограничного слоя пренебречь при определении внешнего потока. Поэтому вязкость жидкости проявляется только в пограничном слое, в рассматриваемой задаче можно принять, что пластина не оказывает никакого влияния на внешний поток и всюду вне пластины от имеет одну и ту же скорость U .

Внешний поток описывается уравнениями Эйлера. Величина производной определяется из уравнения в проекции на ось Ox .

(4.37)

В связи с тем, что в рассматриваемом случае , (на твердой границе), (в силу постановки задачи) левая часть уравнения Эйлера равна нулю и поэтому .

Учтем также, что уравнение неразрывности для пограничного слоя

допускает введение функции тока

(4.38)

,

В этом случае уравнение движения жидкости в пограничном слое принимает вид

(4.39)

Решение этого уравнения должно удовлетворять условиям прилипания на твердой границе погранслоя

(4.40)

,

Последнее условие эквивалентно равенству

(4.41)

На внешней границе погранслоя надо выполнить условия сопряжения потоков по скорости и ее производной по координате . Пусть

(4.42)

уравнение границы погранслоя, форма которой заранее неизвестна и подлежит определению в процессе решения задачи. На этой границе надо выполнит условия

, (4.43)

,

Выполнять условия на неизвестной границе сложно Эту проблему можно существенно упростить, если снести граничные условия с границы

на бесконечно удаленную границу. Такой пограничный слой называется асимптотическим пограничным слоем. При использовании модели асимптотического погранслоя вместо условий (4.43) используются условия

, (4.44)

,

За толщину пограничного слоя при этом можно принять те значения координаты , при которых скорость потока в погранслое мало отличается от скорости внешнего потока, например, на 0.01.

Пусть местная толщина погранслоя. Она имеет величину , как это было установлено, порядка

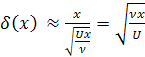(4.45)

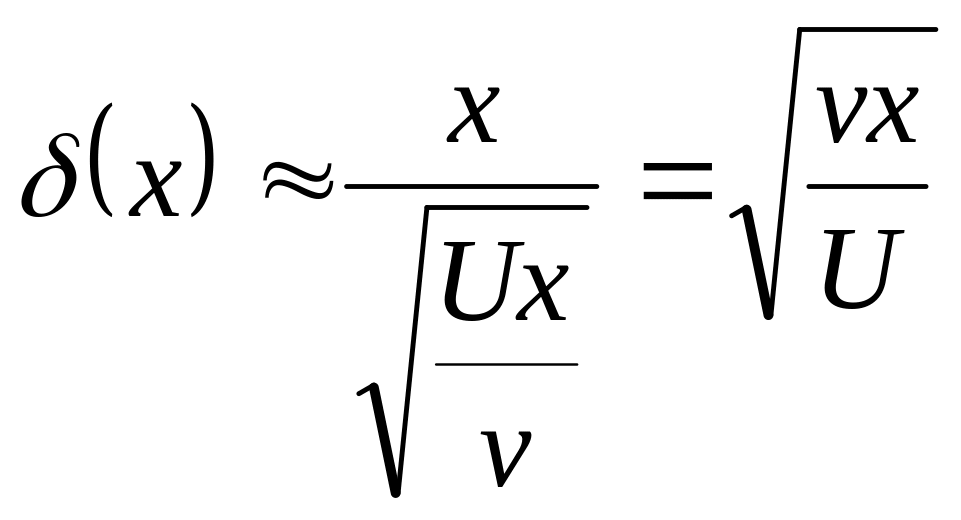
Сделаем замену переменных, положим

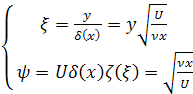(4.46)

Находим

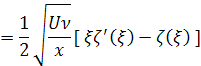
Подставляя вычисленные производные функции в уравнение получаем уравнение

которое после упрощений принимает вид

(4.47)

Граничные условия:

, (4.48)

, ,

Полученное уравнение для функции нелинейное и целесообразно построить его численное решение. Для этого следует свести уравнение(4.47) к системе уравнений первого порядка. Вводим обозначения

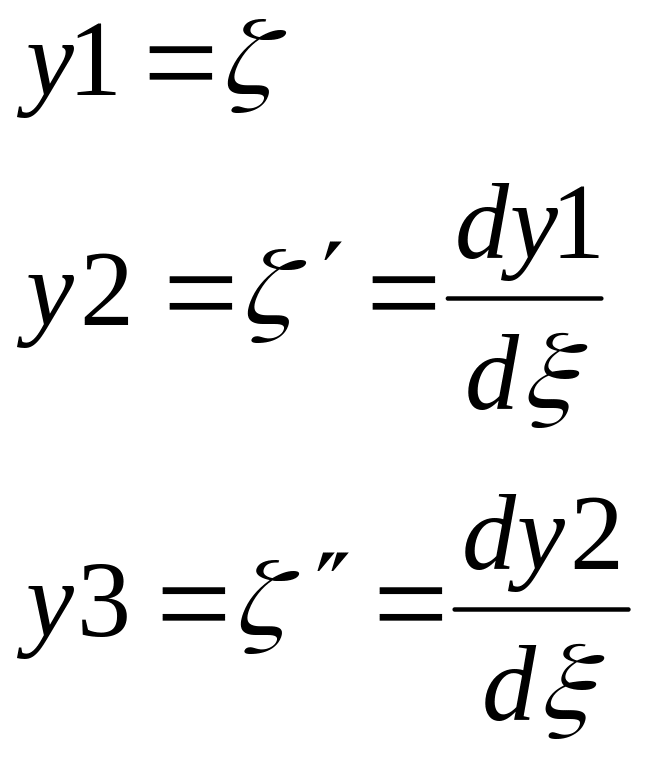
При этом получаем систему уравнений первого порядка

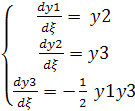(4.49)

Для решения этих уравнений необходимо задать начальные условия, следующие частично из условий (4.48)

, ,

Значение параметра надо подобрать так, чтобы выполнилось условие (4.48) на бесконечности. За бесконечность практически можно принять и удовлетворить условию . Вычисления удобно провести с помощью Maple-программы, приводимой ниже

>restart;

>alpha:=0.332:

>with(DEtools):

>sys := D(y1)(t)=y2(t),D(y2)(t)=y3(t),D(y3)(t)=-1/2.*y1(t)*y3(t);

DEplot([sys],[y1(t),y2(t),y3(t)],t=0..10,[[y1(0)=0,y2(0)=0,y3(0)=alpha]],

scene=[t,y2(t)],method=rkf45,stepsize=0.005,linecolor=black,thickness=1);

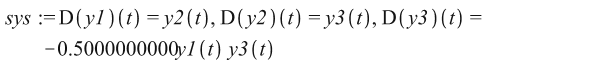
Как видно из полученного графика, при после точки скорость потока становится постоянной и равной , что означает выполнение граничного условия на бесконечности. Если учесть значение переменной . даваемое формулой (4.46), то границе погранслоя отвечает соотношение Следовательно, граница погранслоя описывается уравнением

(4.50)

Основной задачей теории пограничного слоя является определение взаимодействия между потоком жидкости (газа) и телом при больших числах Рейнольдса. Определим силу трения, с которой поток жидкости действует на пластину шириной протяженностью Так как поток плоский, то это взаимодействие определяется по формуле

Напряжение трения на пластине определяется так

Учитывая, что , получаем

Силу трения обычно выражают через коэффициент трения по формуле

где – площадь поверхности тела, соприкасающегося с жидкостью. В рассматриваемом случае пластина своими двумя сторонами соприкасается с жидкостью. Поэтому и легко устанавливается значение коэффициента трения

(4.51)

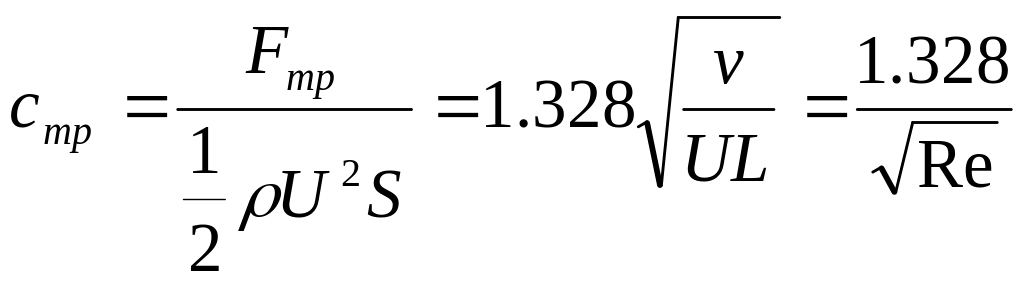
где

Формула (4.51) хорошо согласуется с экспериментальными данными для гладких пластин при .

113 – 122. Набрать формулы в ворде – 2003.

Старые не уничтожать!