3.4. Сходящееся течение в диффузоре при больших числах Рейнольдса
В случае чисто сходящихся течений для решения задачи необходимо учесть, что все корни уравнения (3.21) вещественные, что
(3.31)
выполнить
соответствующие граничные условия
на стенках диффузора и учесть, что на
оси диффузора. При этом
,
,
,
(3.32)
Эти условия можно представить с учетом формулы (3.31) в таком виде
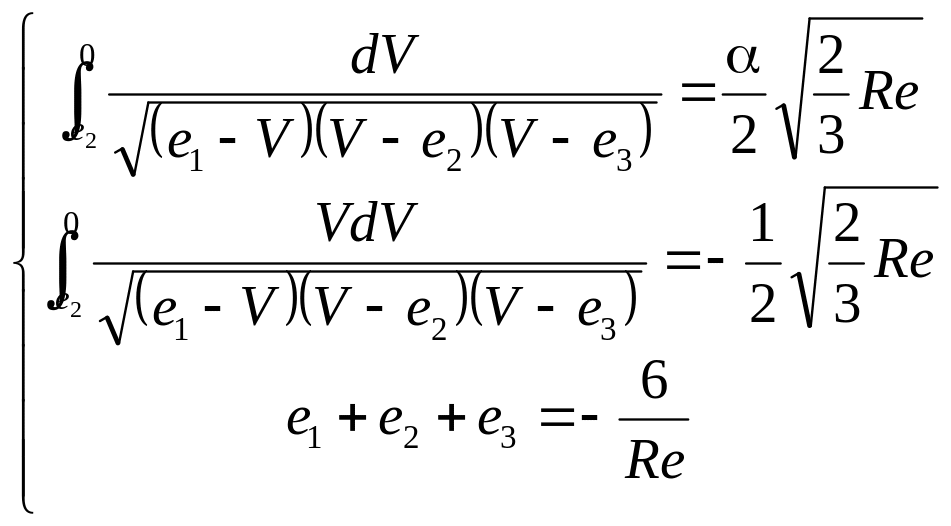(3.33)
Из этих трех
уравнений можно определить три
вещественные постоянные интегрирования
,
где, как ранее было показано, в
рассматриваемом случае
.
Исходя из анализа расходящегося потока интуитивно ясно, что неприятности с решением для сходящегося потока в диффузоре могут возникнуть при больших значениях числа Рейнольдса.
Поэтому покажем,
что система уравнений (3.33) для сходящегося
течения имеет решение и при больших
значениях числа Рейнольдса и найдем
приближенное аналитическое ее решение.
(асимптотическое решение при
).
Обратим внимание на то, что при
(3.34)
а интегралы,
входящие в левые части уравнений (3.33),
становятся расходящимися, что возможно
лишь при
.
В этом случае можно, пользуясь соотношением
(3.34), найти
(3.35)
Основной вклад в значение интегралов (3.33) дает нижний предел, что позволяет положить в числителе второго интеграла . В этом случае второе уравнение, с учетом первого уравнения, при больших числах Рейнольдса приводит к равенству
(3.36)
Это равенство позволяет записать значения всех постоянных интегрирования в случае больших чисел Рейнольдса
(3.37)
При этом уравнение
(3.31) для определения зависимости скорости
от угла 
приобретает вид
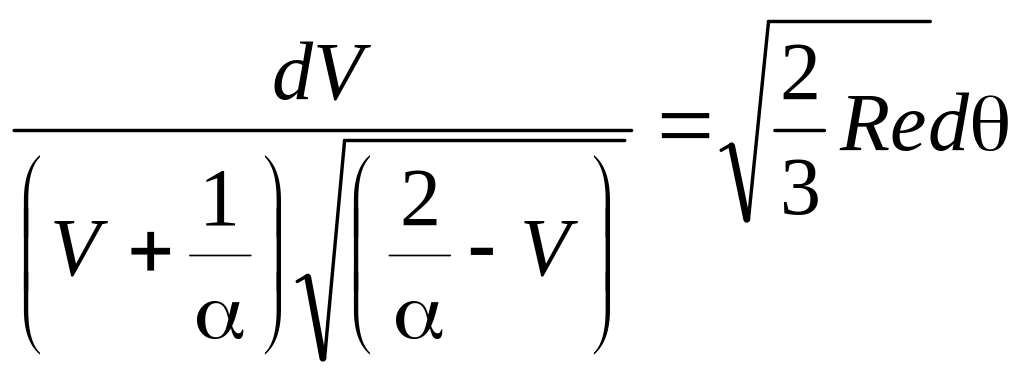(3.38)
Интегрируем полученное уравнение, учитывая граничные условия (3.32), Имеем
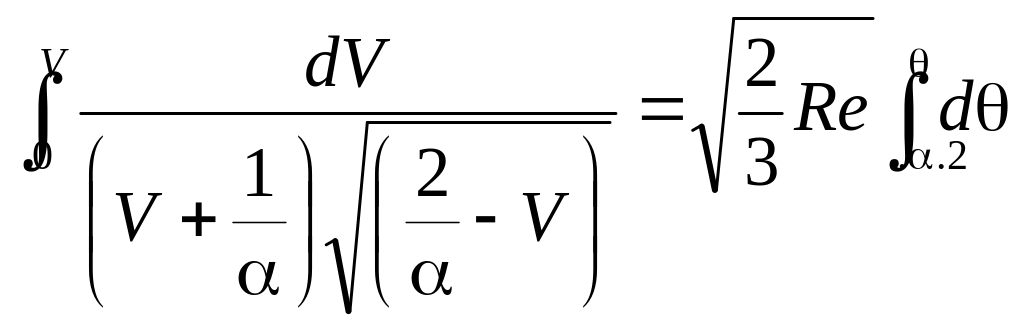(3.39)
Для вычисления интеграла слева используем замену переменной. Полагаем
,
(3.40)
При этом
,
и равенство (339) преобразуется к виду
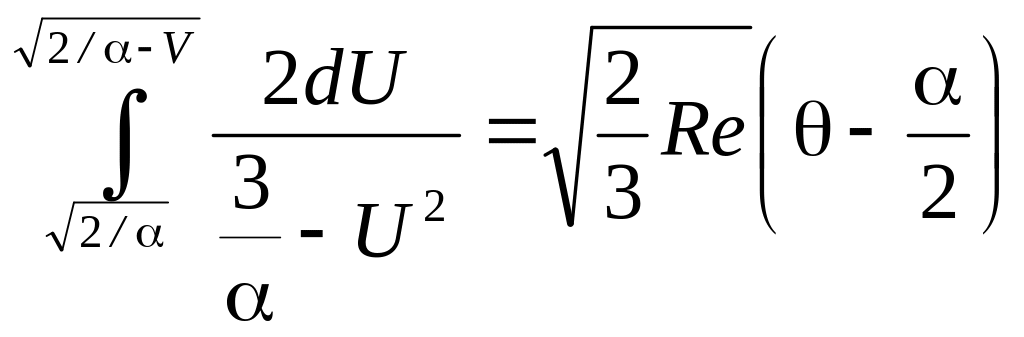(3.41)
Для вычисления интеграла разложим подынтегральную функцию на простые дроби, учитывая, что
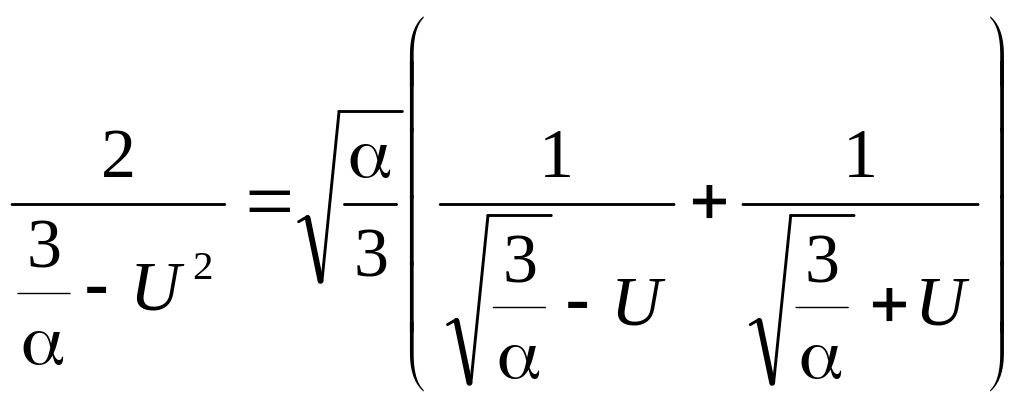
Теперь можно записать равенство (3.41) так
:
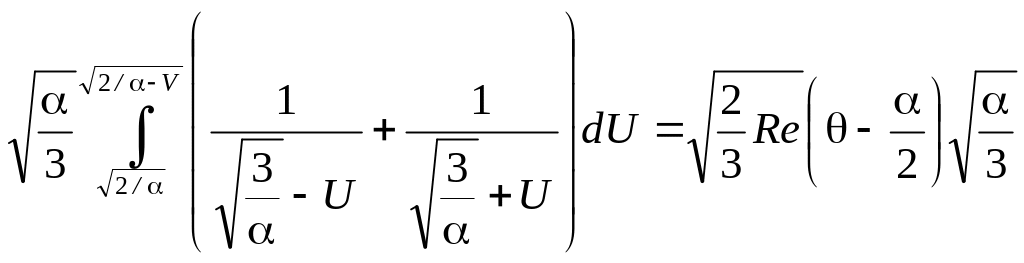
После вычисления интегралов и упрощений получаем равенство
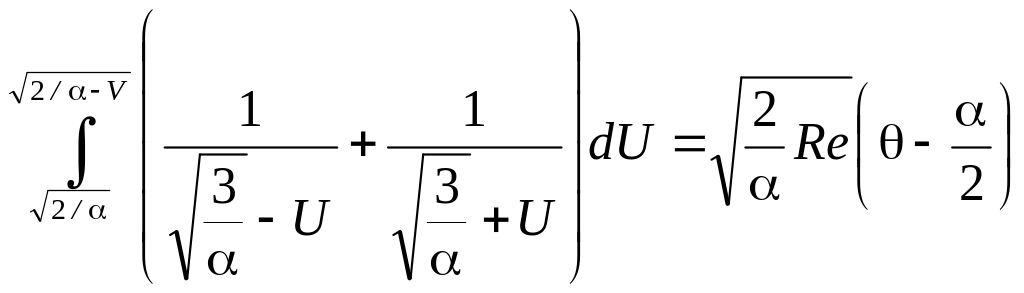
или
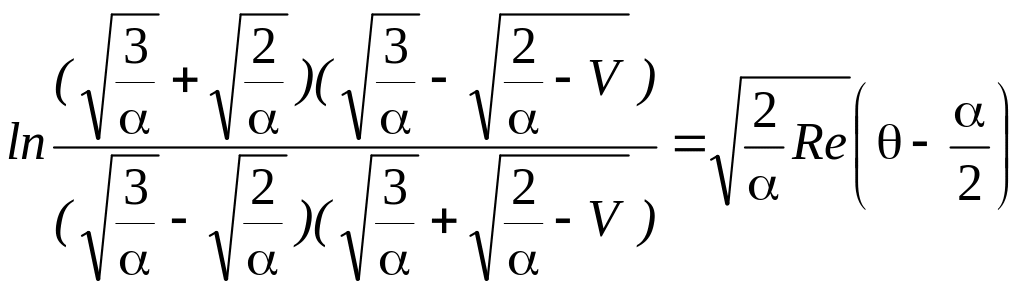
или
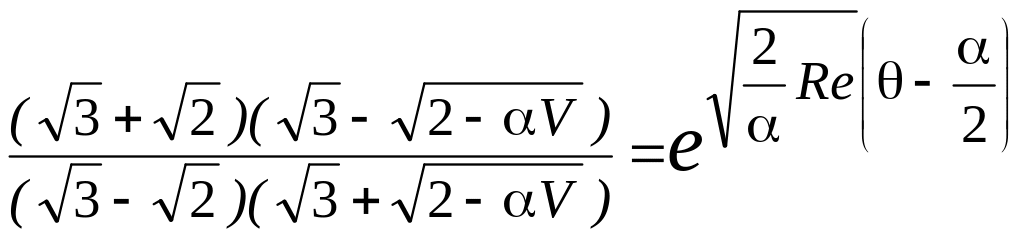(3.42)
Разрешим полученное уравнение относительно . Потенцируя равенство (3.42), находим
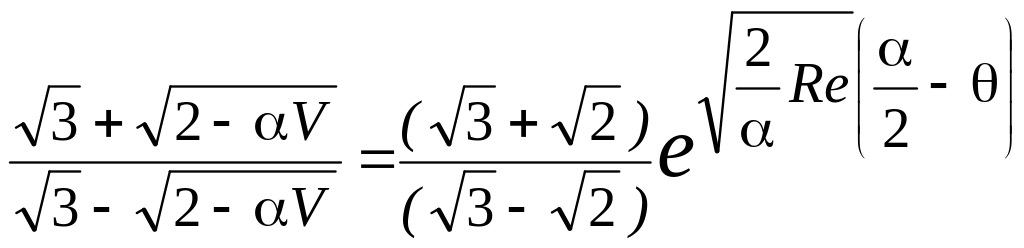
Введем обозначение
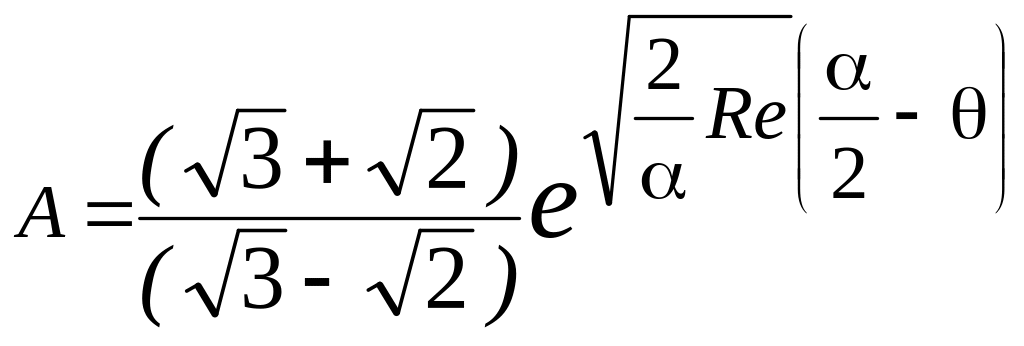(3.43)
получаем уравнение
Отсюда находим
Далее получаем
Это равенство можно записать так
Умножим числитель
и знаменатель дроби на
.
Получим
Совершив последовательно элементарные преобразования, устанавливаем
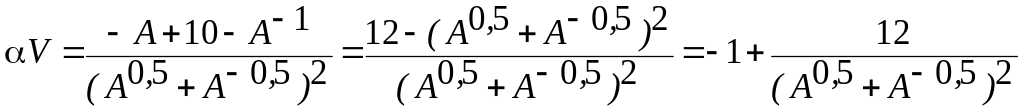
Полученная формула и формулы (3.5) и (3.14), позволяют записать решение задачи о сходящемся течении в диффузоре при больших числах Рейнольдса в таком размерном виде
(3.44)
где в соответствии с формулой (3.43)
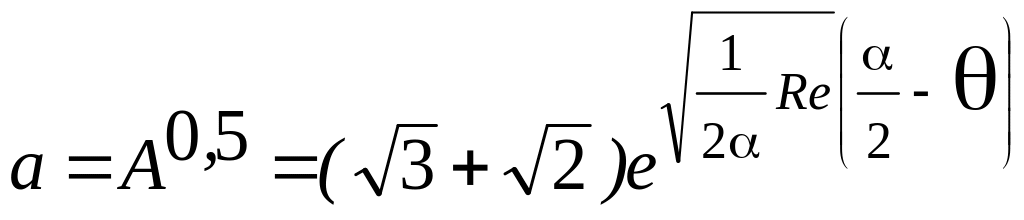
Подчеркнем, что
решение (3.44) получено для той части
диффузора, в которой
Анализировать
полученное решение удобно с помощью
пакета Maple
по приведенной ниже программе, изменяя
значения параметров
и Re.
>
restart: 
:=Pi/3:
Re:=1000:
> a:=(sqrt(3)+sqrt(2))*exp(sqrt(Re/2/α)*(α/2-θ) ):
> v:=-(1.-12/((a+1/a))^2):
plot(v(θ),θ=0..α/2,color=black,thickness=2);
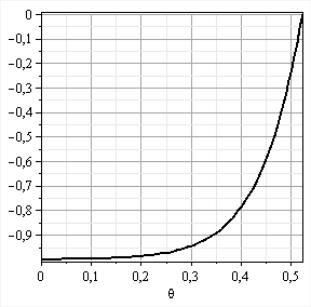
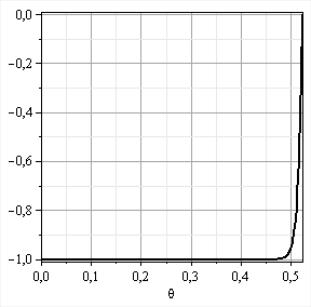
Рис. 3.4. Зависимость от числа Рейнольдса безразмерной скорости в диффузоре при сходящемся течении.
Анализ профилей скоростей, представленный на рис. 3.4, позволяет утверждать, что при больших числах Рейнольдса Re сходящийся поток в диффузоре имеет явно выраженное ядро потока, скорость течения в котором не зависит от угловой координаты и два тонких пристеночных слоя, в которых происходит резкое изменение скоростей от скорости в ядре потока до нуля на его стенках. Эти слои носят название пограничных слоев. Если в ядре потока вязкость жидкости практически не проявляется и жидкость ведет себя как идеальная, то в пограничных слоях вязкость жидкости проявляется существенно. Толщина пограничного слоя в диффузоре может быть оценена ина основе соотношения
~
или
(8.45)
Местная толщина пограничного слоя, оцениваемая по формуле
может быть установлена из условия (3.45). Имеем
(3.46)
Полученная оценка толщины пограничного слоя очевидно не должна зависеть от конкретного течения. Поэтому толщина пограничного слоя, возникающего на поверхности тела при больших скоростях (больших числах Рейнольдса), может быть оценена в общем случае по формуле
(3.47)
где L – характеная протяженнорсть пограничного слоя.
Вне пограничного слоя, в ядре течения, вязкостью жидкости можно пренебрегать и рассматривать ее течение на основе уравнений идеальной жидкости (уравнений Эйлера). При этом, учитывая малость толщины пограничного слоя, наличием пограничного слоя можно пренебрегать при расчете течения в ядре потока.
Течения в пограничном слое подлежит особому исследованию, основы которого излагаются в теории пограничного слоя.