3.2. Математический анализ задачи

При решении задачи обратим внимание на уравнение неразрывности, из которого следует, что

(3.5)

В этом случае уравнение неразрывности выполняется тождественно, а уравнения движения после перехода к функции принимают вид

(3.6)

Интегрируем последнее уравнение, получаем

(3.7)

где - некоторая функция, подлежащая в дальнейшем определению.

После подстановки найденного значения функции p в первое уравнение системы (3.6), получаем

(3.8)

Так как левая часть полученного равенства является функцией переменной , а правая его часть зависит только от r, то такое равенство возможно лишь в случаях, когда обе части уравнения являются постоянными величинами. Обозначим эту постоянную буквой с. Для определения функций u получаем уравнения

(3.9)

Второе уравнение легко интегрируется, в результате чего получаем

что позволяет записать общую формулу для давления

(3.10)

Постоянные c и могут быть найдены, если задать давления в двух точках границы, на которой скорость потока обращается в нуль. Однако при этом нельзя произвольно задать расход жидкости через диффузор, так как расход тесно связан с перепадом давлений вдоль потока, как это показано на примере течения Пуазейля в прямой трубе.

Для интегрирования первого уравнения системы (3.9) умножим его обе части на интегрирующий множитель , получим

После интегрирования этого уравнения находим

(3.11)

где - третья постоянная интегрирования, подлежащая определению.

Разрешая уравнение (3.11) относительно , получаем уравнение

Это уравнение с разделяющимися переменными, что дает возможность переписать его следующим образом

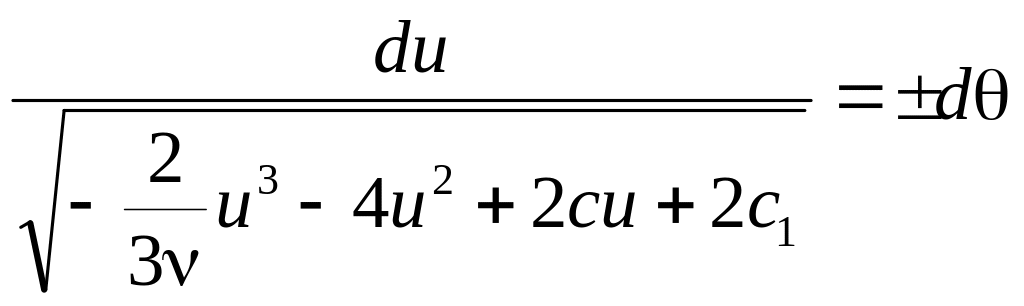(3.12)

Знак “+” здесь соответствует сходящемуся потоку, так как с ростом угла скорость потока в сечении растет (du>0), а знак “-” отвечает расходящемуся потоку (du<0). Дальнейшее аналитическое решение задачи связано с необходимостью интегрирования полученного уравнения. Однако неопределенный интеграл

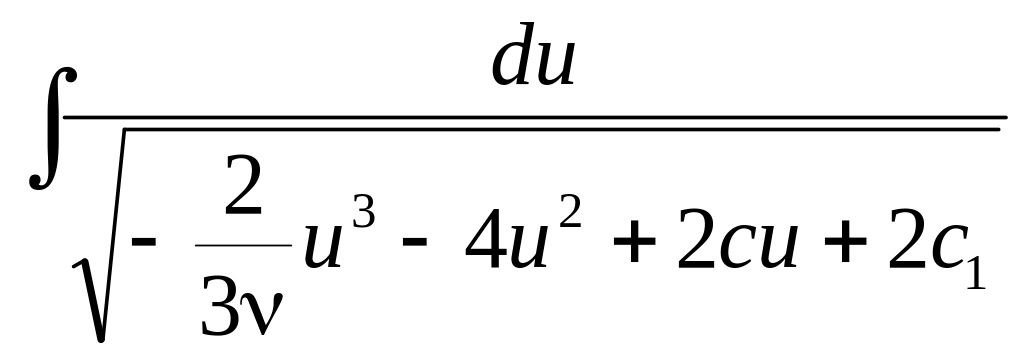, (3.13)

возникающий при таком интегрировании, не может быть определен аналитически при произвольных значениях постоянных и , так как подынтегральная функция содержит квадратный корень из полинома третьей степени, сводящийся к эллиптическому интегралу, квадратура которого, как это следует из теории неопределенных интегралов, не может быть осуществлена в аналитическом виде. Очевидно также, что не при всяких вещественных значениях постоянных и значение интеграла будет вещественным.

В связи со сказанным становится необходимым провести качественный анализ решаемой задачи, который удобно сделать, если предварительно перейти к безразмерным величинам. Положим

(3.14)

При этом исходное уравнение (3.9) преобразуется к виду

(3.15)

где .

Уравнение (3.12) приобретает вид

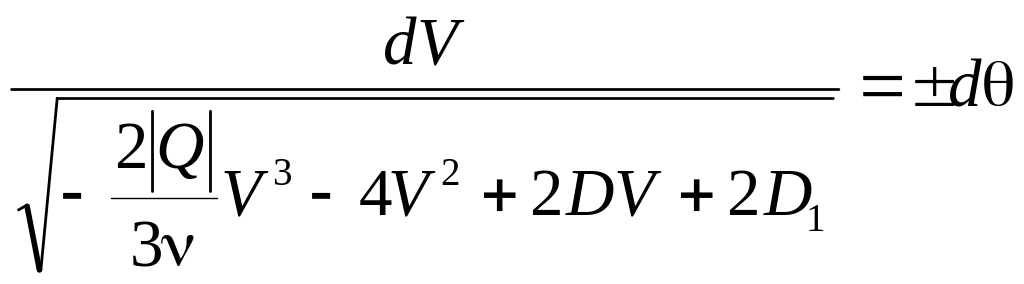(3.16)

где .

Величина есть не что иное, как число Рейнольдса потока жидкости в диффузоре. Поэтому введем обозначение

(3.17)

и перепишем уравнение (3.16) в такой форме

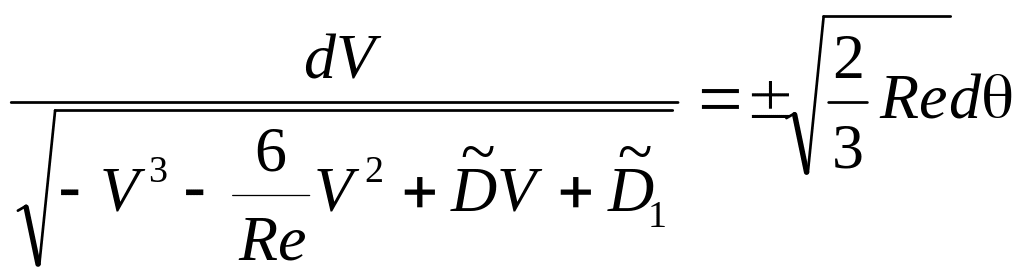(3.18)

где

произвольные постоянные.

Условия, которым должно удовлетворять решение задачи, переписываются в следующем виде

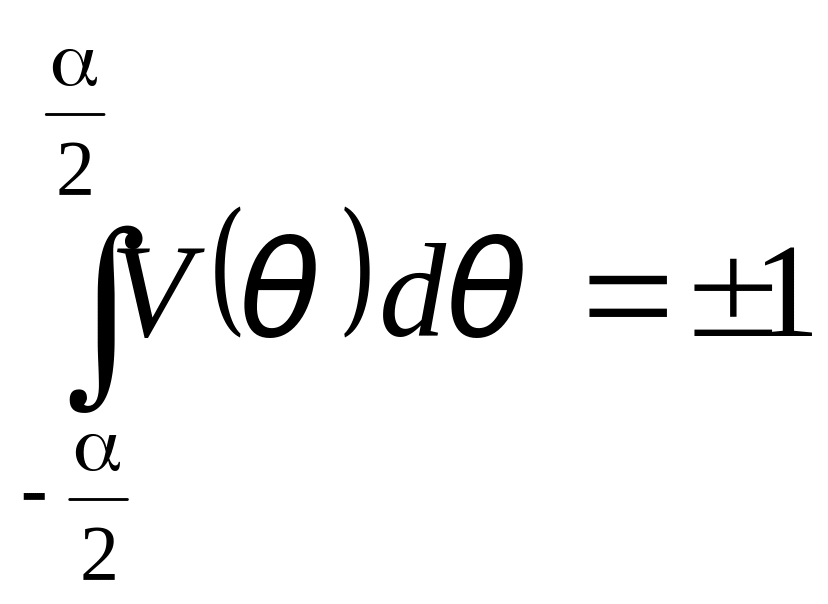, (3.19)

В последней формуле знак “плюс” отвечает расходящемуся течению, знак “минус” - сходящемуся.

Полином, стоящий под радикалом в формуле (3.18), по теореме Виета можно представить в виде произведения линейных множителей

.20)

где , , - корни уравнения

(3.21)

удовлетворяющие условию

, (3.22)

В области, отвечающей реальному течению, должно выполняться неравенство

Для полинома третьей степени с вещественными коэффициентами возможны два случая корней:

а) все корни вещественные. Пусть

б) один корень вещественен, два других – комплексно-сопряженные. Пусть - вещественный корень, а .

Так как и , то в случае а) график функции имеет вид, представленный на рис. 3.2, а в случае б) – на рис..3.3

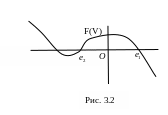
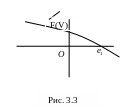
Так как точка должна принадлежать области решения, в которой , то эта точка, согласно рисункам 3.2 и 3.3, должна быть расположена левее точки , что означает, что в любых случаях корней существует область для которой возможно расходящееся течение в диффузоре. Сходящемуся течению отвечают только случаи вещественных корней у функции

Исследование расходящегося течения в диффузоре

В связи с невозможностью построить точное решение задачи ограничимся вначале качественным исследованием расходящегося течения,

для которого уравнение (3.18) принимает вид

(3.23)

причем

и

Для определения величин , , и постоянной интегрирования уравнения (3.23) служат условия

, , (3.24)

которые с учетом величины (3.23) принимают вид

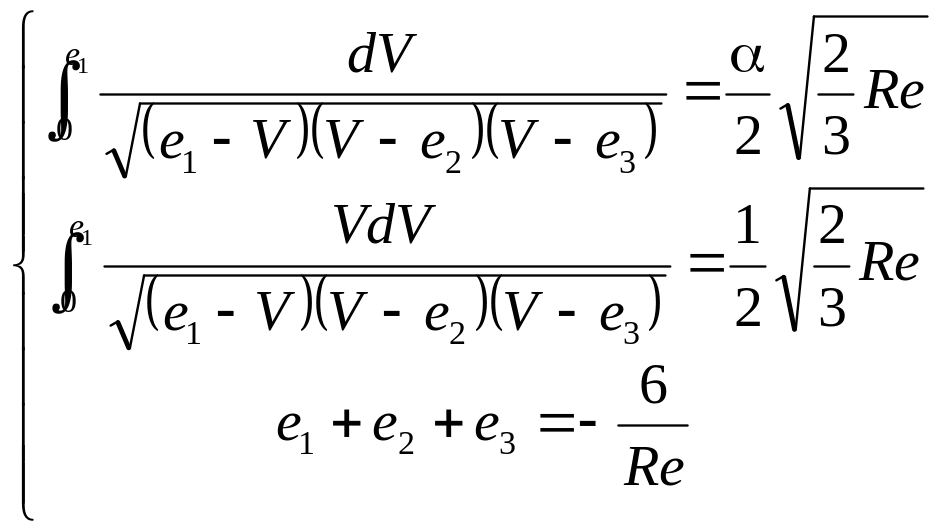(3.25)

Если во втором уравнении (3.25) величину , стоящую в числителе подынтегральной функции, заменить ее максимальным значением , то получим неравенство

(3.26)

Используя первое равенство системы (3.25), неравенство (3.26) можно преобразовать к виду

из которого следует, что при расходящемся течении должно выполняться неравенство

(3.27)

Еще одно условие, которое должно выполняться для реализации чисто расходящегося течения, можно получить, если оценить интеграл, входящий в первое уравнение системы (8.25), учитывая неравенство

Вследствие этого имеет место неравенство

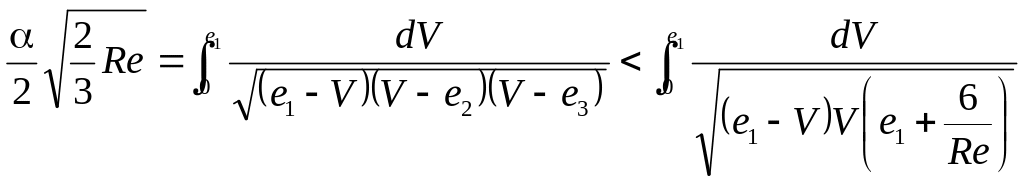(3.28)

Последний интеграл легко вычисляется, если учесть, что

При этом имеем

=

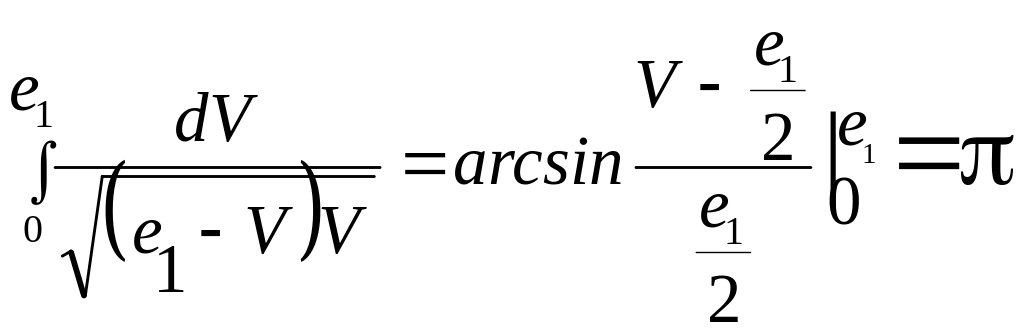Поэтому согласно (3.27) имеет место неравенство

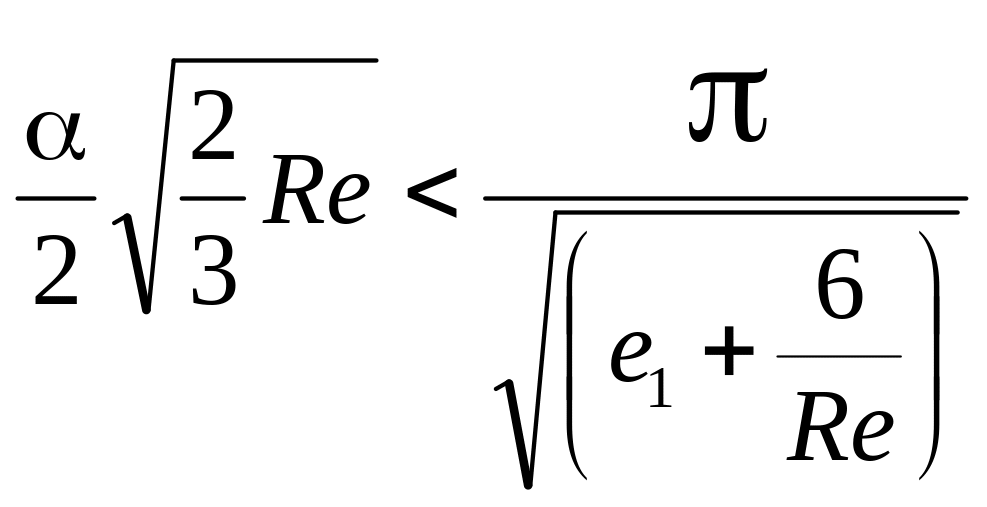
Откуда вытекает условие, налагаемое на угол раствора диффузора,

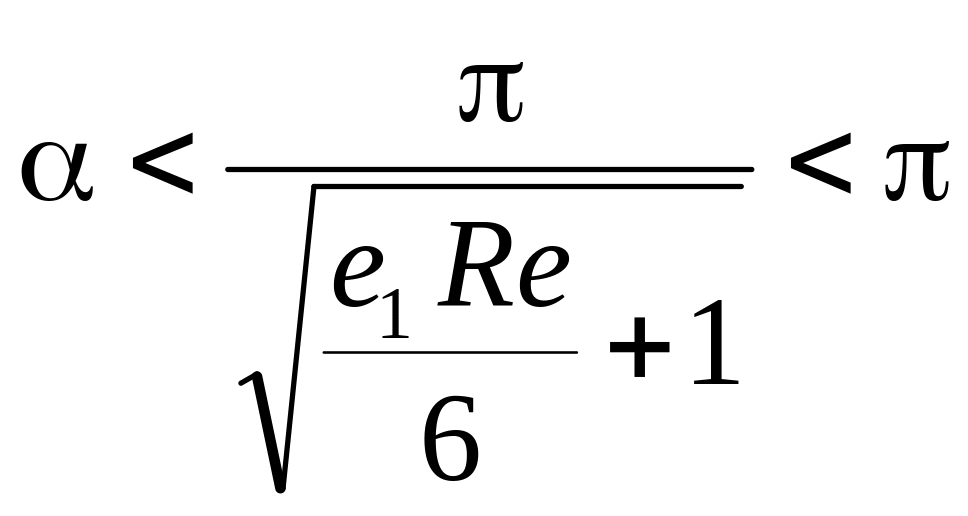(3.29)

из которого следует

Учет неравенства (3.27) при этом позволяет получить ограничение на значения чисел Рейнольдса, при которых возможно чисто расходящееся течение в диффузоре

(3.30)

Подводя итоги исследованию чисто радиальных расходящихся течений в плоском диффузоре, можно заключить, что они возможны только в случаях углов раствора меньших и при этом при малых числах Рейнольдса, значения которых должны удовлетворять неравенству (3.30). Если указанные ограничения нарушаются, то это означает, что допущение о чисто радиальном расходящемся течении неприемлемо и что расходящееся течение в диффузоре обязательно должно сопровождаться появлением зон поперечного течения, а поток становится двумерным.

.