2.5. Одномерное течение вязкой жидкости между вращающимися твердыми круглыми соосными цилиндрами

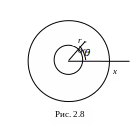Рассмотрим течение жидкости полностью заполняющей зазор между вращающимися бесконечно длинными цилиндрами (рис.2.8). Пусть a- радиус внутреннего цилиндра, _b – внешнего, a и , соответственно, постоянные угловые скорости вращения цилиндров. Такая задача частично моделирует явления, происходящие в смазочных слоях цилиндрических подшипников скольжения, и поэтому имеет большое практическое значение. В более общей постановке, учитывающей скольжение жидкости по поверхностям цилиндров, а не прилипание к ним, задача впервые была поставлена и решена Николаем Павловичем Петровым (1836 г.,— 1920 г.) — крупным российским ученым и инженером, профессором, инженер–генерал-лейтенантом, почетным членом Петербургской А.Н., основоположником гидродинамической теории смазки, впервые в истории применившим уравнения движения вязкой жидкости к решению технических задач.

Используем цилиндрические координаты . Допускаем, что линии тока частиц жидкости - окружности, лежащие в плоскостях перпендикулярных осям цилиндров. В этом случае из трех компонент скорости только одна ( ) отлична от нуля. Учитывая осевую симметрию потока., принимаем .. Записываем уравнения Навье-Стокса

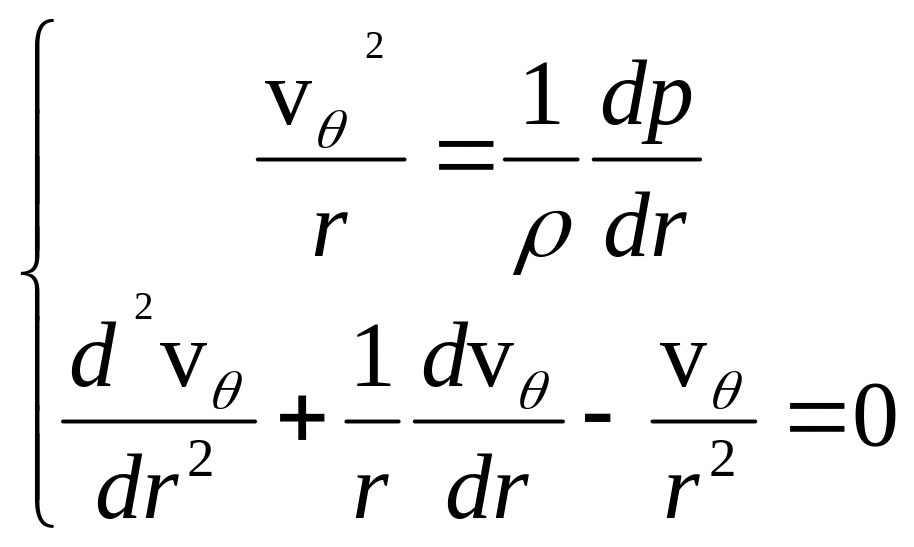(2.61)

и граничные условия:

Второе уравнение интегрируется независимо от первого. Оно для является однородным уравнением типа Эйлера, Его решения отыскиваются в виде

=

Подставляя это значение в уравнение () получаем характеристическое уравнение

решениями которого являются .и Поэтому общее решение уравнения имеет вид

(2.62)

Выполнение граничных условий приводит к системе уравнений

=

Находим

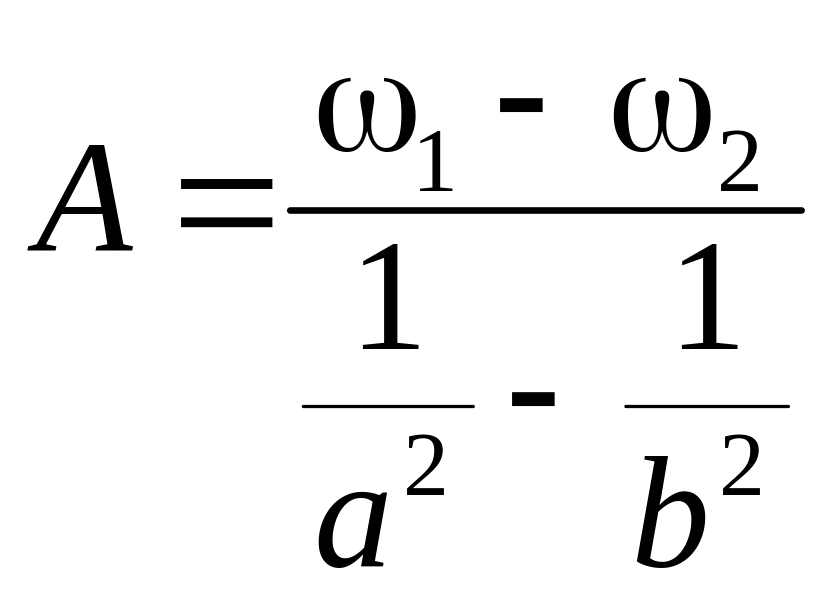
(2.63)

Важной характеристикой цилиндрических подшипников является момент сил трения, действующих на шип (внутренний цилиндр) и порожденных касательными напряжениями со стороны жидкости (см. (1.22))

Момент этих сил трения, приходящихся ,на единицу длины цилиндра, вычисляется по формуле

(2.64)

На внешний цилиндр действует такой же момент сил, но противоположного знака

(2.65)

На преодоление сил трения необходимо затратить энергию, вычисляемую за единицу времени на единицу длины цилиндров по формуле

Учитывая значение коэффициента , получаем

(2.66)

Проанализируем частные случаи полученного решения

1. Случай вращения цилиндра в безграничной жидкости.

Положим и устремим b к бесконечности. При этом получаем

(2.67)

Как нетрудно усмотреть, течение вязкой жидкости вне цилиндра является потенциальным, соответствующим прямолинейной вихревой нити с циркуляцией . Такие течения наблюдаются и в вязком газе, что подтверждается натурными наблюдениями над торнадо.

2. Случай малого зазора.

Полагаем , и проводим линеаризацию формулы (2.66). Получаем знаменитую формулу Петрова

(2.68)

По этой формуле рассчитываются потери энергии, расходуемой на поддержание вращения роторов турбин энергетики, самолетов, мореходной техники и т.п., в соответствии с чем устанавливаются потребности в изыскании и создании новых источников энергии и энергетических установок в государственных и мировых масштабах. Снижение потерь на трение является государственной и международной проблемой.

В заключение определим распределение давлений в зазоре. c учетом вида функции . Имеем

После интегрирования этого уравнения получаем

Как видим, за счет центробежного эффекта давление меняется вдоль радиуса. Оценим этот эффект для случая малого относительного зазора. Положим и примем при этом , а для упрощения вычислений рассмотрим случай, когда вращается только внутренний цилиндр. Вычисления осуществим с помощью пакета Maple по приводимой ниже программе

> restart:

> b:=a+delta:

> A:=(omega0-omega1)/(1/a^2 -1/b^2):

> B:=(omega1*b^2-omega0*a^2)/(b^2-a^2):

> omega1:=0:

> r:=a+delta*zeta:

> p:=ρ*series(-A^2/(2*r^2 )+2*A*B*ln(r/a)+B^2*r^2/2,delta,5)+C;

Как видим, изменения давления поперек слоя оказываются пренебрежимо малыми, имеющими порядок gо сравнению с главным (первым) членом разложения, не зависящим от переменной . Поэтому в случаях малых зазоров можно принять , что и используется в теории смазки.