МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

Факультет Прикладной математики и физики

Кафедра 801

Курсовая работа

по дисциплине физика

Тема: Электромагнитные колебания

Вариант №16

Студент: Ломакин Антон Подпись:

Группа: 4O – 109Б

Руководитель работы: Поярков И.В.

Оценка:

Дата:

Подпись преподавателя

Москва 2013

Содержание

1. Теоритический вопрос 3

   1. Электромагнитные колебания. 3

   2. Свободные затухающие электромагнитные колебания, уравнение затухающих колебаний, анализ его решения. Условие существования электромагнитных колебаний в реальном колебательном контуре. Частота затухающих колебаний. Критическое сопротивление контура. Характеристики затухающих колебаний (время затухания, логарифмический декремент затухания, добротность контура). 6

2. Задача №1 8

3. Задача №2 12

4. Задача №3 13

5. Задача №4 14

6. Задача №5 16

7. Задача №6 17

8. Задача №7 18

9. Задача №8 19

10. Задача №9 21

11. Список используемой литературы 22

1. Теоретический вопрос

1.1 Электромагнитные колебания

Колебания – повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Свободными колебаниями называются колебания, которые возникают в системе, не подверженной действию переменных внешних сил, в результате какого – либо однократного начального отклонения этой системы от состояния равновесия.

Затухающими называются колебания, энергия которых уменьшается с течением времени. Затухание свободных гармонических колебаний связано с убылью энергии колеблющейся системы за счет действия сил трения и других сил сопротивления.

Электромагнитные колебания - взаимосвязанные колебания электрического и магнитного полей.

Основная задача в теории электромагнитных колебаний заключается в нахождении закона изменения во времени какой-либо электрической или магнитной физической величины. При исследовании электромагнитных колебаний в физическую систему обычно включают электромагнитное поле и тела в которых оно локализовано. Электрические и магнитные колебания взаимосвязаны. Поэтому говорят об электромагнитных колебаниях.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

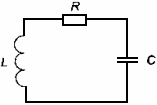Колебательным контуром называется электрическая цепь, состоящая из последовательно соединенного конденсатора с емкостью C, катушки с индуктивным сопротивлением L и электрического сопротивления R. (рис. 1)

В колебательном контуре могут происходить периодические изменения заряда q, разности потенциалов на обкладках конденсатора и электрического тока I в цепи. Если эти изменения вызваны тем, что на обкладки конденсатора однократно заряжаются, то в колебательном контуре (рис.1) возникают свободные электромагнитные колебания.

В реальном колебательном контуре (R≠0) свободные электромагнитные колебания являются затухающими. Например, изменение заряда q на обкладках конденсатора описывается формулой, аналогичной уравнению затухающих механических колебаний

(рис. 2)

Где – амплитудное значение заряда в момент времени t=0;

Формула (1.1) выражает коэффициент затухания (R- электрическое сопротивление, L- индуктивность контура); - начальная фаза колебаний заряда.

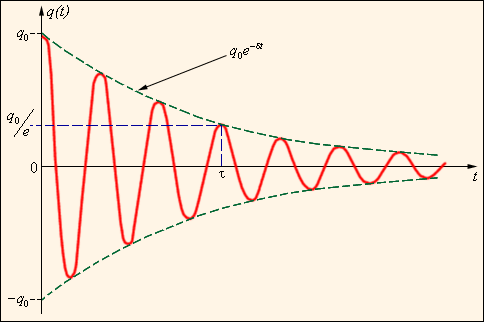
На рисунке изображена зависимость q от t в таком колебательном контуре.

(рис.3)

Напишем для цепи /—3—2 (рис.3) выражение закона Ома, которое примет вид:

Разделив это уравнение на L и заменив I через q, а через получим:

Приняв во внимание, что величина, обратная , равна квадрату собственной частоты контура

и введя обозначение

получим уравнение

при решение уравнения (1.6) умеет вид:

где и – постоянные определяемые из начальных условий;

- амплитуда затухающих колебаний.

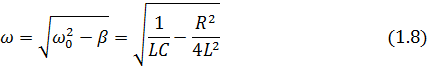
Ф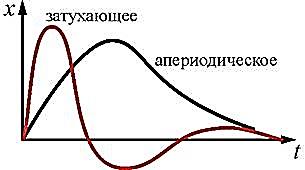 ормулой (1.8) выражается частота затухающих колебаний.

(рис. 4)

При , вместо колебаний происходит апериодический разряд конденсатора. Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим.

2. Характеристики затухающих колебаний

Коэффициент затухания величина, обратная времени релаксации , за которое амплитуда колебаний уменьшится в е раз.

Логарифмический декремент затухания - величина обратная числу колебаний, совершаемых за время релаксации и описывает уменьшение амплитуды колебательного процесса и равна натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону.

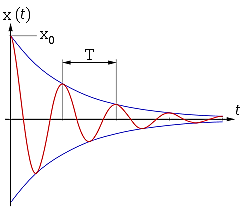
(Рис. 5)

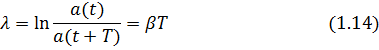
Подставив в уравнение (1.14) β и заменив , получим:

Частота , а следовательно и 𝜆 определяются параметрами контура L, C и R. Таким образом, логарифмический декремент затухания является характеристикой контура.

Если затухание велико ), можно положить в (1.15)

Тогда

Добротность – свойство колебательной системы, определяющее полосу резонанса и показывающее, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Величина обратно пропорциональная логарифмическому декременту затухания

Из данной формулы следует, что добротность контура тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в е раз.

В случае слабого затухания: