1.3 Загальне формулювання і приклади задач лінійного програмування

У загальному формулюванні зворотну задачу лінійного програмування (ЛП) можна записати так: знайти значення керованих змінних х1, х2, ..., хn , при котрих їх лінійна функція

С₁ х₁ + С₂ х₂ + ... + С_n х_n

приймає максимальне (мінімальне) значення, а також задовольняються функції – обмеження

a₁₁ х₁ + а₁₂ х₂ + ... а_1n x_n  в₁,

a₂₁ х₁ + а₂₂ х₂ + ... а_2n x_n = в₂,

………………………………

a_m1 х₁ + а_m2 х₂ + ... а_mn x_n  в_m,

х _і  0, і =1,n

У наведеному запису задачі знаки рівностей і нерівностей між лівими і правими частинами функцій-обмежень вибрані довільно.

Основна особливість будь-якої задачі ЛП полягає в тому, що в ній кількість змінних більше кількості функцій-обмежень. Тому задача ЛП має, як правило, безліч допустимих розв’язків, з яких треба визначити оптимальний, а іноді - раціональний, найкращий з допустимих.

Обмеження на значення керованих змінних, що вимагають їх невід’ємності, обумовлені тим, що ці змінні звичайно є фізичними величинами, які не можуть бути від’ємними: час, кількість повітряних суден, відстань тощо. Разом з тим треба відзначити, що це стосується тільки задач практичної діяльності людини, в теорії ЛП такі обмеження не завжди враховуються.

Постійні в задачі лінійного програмування мають такі назви: Сі, і=1,n - оцінки задачі, тому що ці постійні немов би “оцінюють” значущість відповідних керованих змінних в цільовій функції; аіj, і=1,n, j=1,m - коефіцієнти задачі; вj, j=1,m - ресурси задачі.

Постійні задачі ЛП також не можуть бути від’ємними, оскільки в задачах практики вони є певними фізичними величинами. Це може бути вартість польоту повітряного судна протягом певного часу або на певну відстань, вантажопідйомність судна тощо.

Як відзначалося вище, будь-які задачі, що пов’язані з практичною діяльністю людини, спочатку формулюються оповідально (словесно), а вже потім “перекладаються” мовою математики, тобто записуються формально. Як приклади, наведемо словесні формулювання деяких задач ЛП, що розв’язуються у процесі обслуговування повітряного руху. При цьому будемо вважати, що безпека польотів не залежить від варіанту розв’язку задачі, в якій цільова функція передбачає забезпечення максимуму економічності польотів.

В штатних умовах управління повітряним рухом два повітряних судна одночасно претендують на виконання посадки при наявності на аеродромі однієї злітно-посадкової смуги. Необхідно визначити раціональну черговість посадки суден (мова може йти тільки про раціональну черговість, тому що оптимальним був би варіант, що передбачає одночасну посадку обох суден). Оскільки вважаємо, що безпека польотів не залежить від черговості посадки суден, то цільова функція повинна передбачати мінімізацію витрат, пов’язаних з польотом суден, зокрема, це можуть бути витрати пального. При цьому змінними буде час польоту одного і іншого судна, значення змінних залежать від черговості посадки суден. Формально обмеження на значення змінних обумовлені наступним: мінімальний час польоту судна не може бути меншим того, який необхідний для заходження на посадку і виконання посадки; максимальний час польоту обмежується наявною кількістю пального на борту.

Задача визначення раціональної черговості посадки двох повітряних суден розв’язується як пряма задача математичного програмування: знаючи час польоту суден для одного і іншого варіанту черговості посадки (він залежить від мінімальних допустимих інтервалів між посадками, тобто від типів суден) і витрати пального за одиницю льотного часу, обчислюють сумарні витрати для одного і іншого варіанту і вибирають той з них, який забезпечує менші витрати.

До типових задач лінійного програмування можна віднести задачу розподілу потоків повітряних суден на “паралельні” ділянки повітряних трас, коли протяжності таких ділянок різні, а пропускна спроможність спрямної ділянки обмежена. Цю задачу розв’язують у процесі планування повітряного руху на етапі формування потоків повітряних суден. Цільова функція задачі передбачає забезпечення максимальної економічності польотів, а обмеження вимагають наступного:

- інтенсивність польотів на спрямній ділянці повітряної траси не повинна перевищувати допустиму;

- сумарна інтенсивність польотів на “паралельних” ділянках повинна бути не менше заданої (необхідної).

Зауважимо, що вживане вище поняття “паралельні ділянки” не відповідає геометричному, тут воно означає, що осі симетрії таких ділянок виходять з однієї точки і сходяться в іншій одній точці, але можуть бути ломаними лініями.

Типовою задачею лінійного програмування є також задача розподілу повітряних суден за повітряними лініями (маршрутами), сутність якої полягає у наступному.

Експлуатант має певну кількість повітряних суден різних типів, з використанням яких треба виконати авіаційні перевезення на заданих авіалініях (маршрутах) протягом заданого часу. Відомі: прибуток, який забезпечується використанням одного повітряного судна кожного типу на кожній авіалінії, наявна кількість повітряних суден кожного типу, наявні обсяги перевезень на кожній авіалінії. Експлуатант хоче максимізувати прибуток шляхом відповідного розподілу суден за авіалініями, а також зобов’язаний виконати перевезення в наявному обсязі. В цій задачі цільова функція передбачає максимізацію прибутку, а функції - обмеження враховують наявні кількість суден кожного типу і обсяг перевезень на кожній авіалінії.

Можна навести інші приклади задач лінійного програмування, що відносяться до процесів обслуговування повітряного руху або експлуатації повітряних суден.

1.4 Графічне розв’язання задачі лінійного програмування

Графічним способом можна розв’язати тільки задачі ЛП з двома невідомими.

Як приклад, розглянемо розв’язання графічним способом наступної задачі.

Необхідно виконати перевезення обсягом 24 умовні одиниці, використовуючи для цього повітряні судна двох типів і забезпечивши максимальний прибуток. Відомі також такі дані (далі один тип повітряних суден означений 1, а інший - 2, всі величини, крім кількості суден, наведені в умовних одиницях):

Тип повітряного судна	1	2
Кількість суден	6	8
Продуктивність одного судна протягом часу, що розглядається	3	2
Прибуток за рахунок використання одного судна	30	15

Аналітичний запис задачі:

30х₁+15х₂  max - цільова функція задачі,

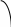
3x₁+2x₂  24,

x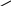 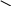₁  6, обмеження

x ₂  8 задачі

x₁  0, x₂  0

Графічним способом задача ЛП розв’язується у такому порядку.

В системі координат Х1ОХ2 (рис. 1.2) проводимо прямі лінії, що відповідають обмеженням задачі, спочатку враховуючи при цьому тільки знаки рівності. Потім, враховуючи в обмеженнях задачі знаки нерівностей, робимо штриховку з того боку кожної прямої, де розташовані допустимі значення змінних x1, x2. Так одержимо область допустимих значень змінних, яка на рисунку двічі заштрихована.

Після цього прирівнюємо цільову функцію довільному числу і в тій же системі координат проводимо пряму, що відповідає прийнятому значенню цільової функції. В прикладі, що наводиться, прийняте значення цільової функції дорівнює 90.

Очевидно, чим більше значення матиме цільова функція, тим далі справа розміститься пряма цільової функції, зміщуючись при цьому паралельно сама собі. Отже, з одного боку, бажано щоб ця пряма була розташована якнайдалі справа, а з іншого боку, вона при цьому повинна мати хоча б одну загальну точку з областю допустимих розв’язків задачі, координати якої і будуть оптимальним розв’язком. На малюнку бачимо, що точкою області допустимих розв’язків, яка максимально віддалена від прямої 30х1+15х2=90, є точка перетину прямих 3х1+2х2=24 і х1=6, вона означена А. Розв’язавши систему рівнянь цих двох прямих, визначимо координати точки А: х1=6, х2=3. При цьому цільова функція приймає значення 225.

Очевидно, можливий випадок, коли пряма цільової функції паралельна одному з відрізків, що обмежують область допустимих розв’язків задачі. Тоді говорять, що рівняння двох таких прямих лінійно залежні, тому що одне з них можна одержати, помноживши або розділивши ліву і праву частини іншого на певне число. Зокрема, у наведеному вище прикладі це мало б місце, якби ліва частина цільової функції мала вигляд 30х1+20х2, тобто була лінійно залежною з функцією-обмеженням задачі 3х1+2х224. При цьому оптимальним рішенням задачі були б координати будь-якої точки відрізка, що на малюнку означений АБ. У нашому прикладі це означало б, що перевезення виконувати було б однаково вигідно з використанням повітряних суден обох типів.