Запитання для самоконтролю

1. Поясніть, в чому полягають взаємозв’язок і відмінність понять “дія” і “діяльність” людини-оператора.

2. Перерахуйте основні етапи діяльності людини-оператора, сформулювавши мету і зміст етапу, дії оператора і фактори впливу на кожному етапі.

3. Наведіть основні різновиди операторської діяльності і сутність (особливість) кожного з них.

4. Наведіть приблизне співвідношення обсягів інформації, що сприймається з допомогою різних аналізаторів людиною.

5. Наведіть означення диференційного порогу розрізнення рівнів сигналів людиною.

6. Наведіть означення оперативного порогу розрізнення рівнів сигналів людиною.

7. Від чого залежить видимість того чи іншого предмета (світлового сигналу)?

8. Поясніть поняття “прямий контраст” і “зворотний контраст” світлових сигналів. При якому контрасті забезпечуються кращі умови для прийому сигналів?

9. Який темп передачі мовного сигналу вважається (приблизно) оптимальним і який - прийнятним (допустимим)?

10. При якій довжині (кількості слів) мовної фрази її довжина не впливає на якість прийому сигналу?

11. Як під час ведення радіозв’язку дотримання інтервалів між словами і словосполученнями впливає на якість прийому?

12. Як залежить час, що витрачається людиною-оператором на упорядкування взаємного положення об’єктів (наприклад, повітряних суден), від кількості таких об’єктів?

13. Поясніть, який взаємозв’язок існує між потенційною продуктивністю праці і ймовірністю своєчасних та безпомилкових дій людини-оператора у процесі розв’язання функціональних задач.

14. Наведіть (приблизно) і поясніть графік залежності ймовірності своєчасного і безпомилкового розв’язання функціональних задач людиною-оператором від наявного часу.

6 Розв’язування задач обслуговування повітряного руху методами теорії графів

6.1 Основні відомості і приклад задачі

У процесі розв’язування задач обслуговування повітряного руху часто виникає необхідність розглядати об’єкти, що певним чином з’єднані між собою : абоненти системи зв’язку, аеродроми тощо. При цьому доцільно, як правило, використати графічне умовне зображення таких об’єктів і ліній зв’язку між ними. Тоді матимемо систему, що складається з точок і ліній зв’язку, яку у загальному випадку називають графом. В свою чергу, точки графа називають його вершинами, а лінії – ребрами.

Метою застосування графів може бути :

- забезпечення наочності при розв’язуванні задач без застосування методів теорії графів, тобто при розв’язуванні задач іншими методами;

- розв’язування таких задач методами теорії графів, які іншими методами розв’язуються більш складно або й зовсім не можуть бути розв’язані, зокрема, до останніх відносяться задачі визначення пропускної спроможності мережі повітряних трас, визначення маршруту максимальної завантаженості повітряного судна, визначення на мережі повітряних трас маршруту мінімальної протяжності, що з’єднує два аеродроми, тощо.

Розглянемо приклад задачі, яка порівняно просто може бути розв’язана тільки методами теорії графів.

Допустимо, що в аеропорту потрібно з’єднати лінією зв’язку ряд пунктів (точок). Природно, конфігурацію лінії треба вибрати такою, щоб загальна протяжність лінії була найменшою з усіх можливих. Очевидно, аналогічну задачу матимемо, якщо поставимо за мету забезпечити мінімальну вартість лінії. Зрозуміло, що відстані між точками, які підлягають з’єднанню, відомі, а у випадку розгляду вартості лінії попередньо розраховуються вартості ділянок лінії, які з’єднували б кожну точку з усіма іншими.

Якщо означену вище задачу розв’язувати шляхом перегляду всіх можливих варіантів, то треба буде виконати великий обсяг обчислень, тому що при дев’яти пунктах, що потребують з’єднання, кількість варіантів їх з’єднання складає кілька сотень тисяч. Разом з тим така задача порівняно просто розв’язується методами теорії графів. При цьому порядок її розв’язування полягає у наступному :

- схематично, у вигляді точок зображаємо пункти, що підлягають з’єднанню (рис. 6.1), при цьому співвідношень між відстанями дотримуватися не обов’язково, тобто відстані між точками на такій схемі можуть бути довільними (згідно з рис. 6.1 розглядаємо задачу єднання п’яти пунктів, які означені А1, А2, А3, А4 і А5).

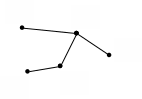- складаємо таблицю відстаней між пунктами, які необхідно з’єднати ( l - відстань між i-м і j-м пунктами, i = , j = , i  j ) :

	A	A	A	A	A
A	___	a12	a13	a14	a15
A	___	___	a23	a24	a25
A	___	___	___	a34	a35
A	___	___	___	___	a45
A	___	___	___	___	___

- з таблиці вибираємо найменше число a і на рис. 6.1 з’єднуємо відрізком прямої точки, що відповідають цьому числу, зокрема, якщо таким числом є відстань a , то з’єднуємо точки A і A ; далі вибираємо наступне найменше число і з’єднуємо відповідні йому точки і т.д. до тих пір, поки лінія зв’язку не з’єднає всі пункти;

- якщо у процесі розв’язування задачі виявиться, що чергове найменше число передбачає з’єднання пунктів, які вже з’єднані через інший, третій пункт, то таке з’єднання не враховується; наприклад, якщо вже маємо лінію, що з’єднує точки A , A і A і черговим найменшим числом виявилося число a34, то це число не враховуємо, тобто точки A і A не з’єднуємо, тому що вони вже з’єднані між собою через точку A .

З використанням методів теорії графів розв’язується багато задач обслуговування повітряного руху, при цьому такі методи часто використовуються разом з методами теорії систем масового обслуговування і ін.

6.2 Основні означення

Часто зв’язки між вершинами графа орієнтовані за напрямом, тоді такий напрям означають стрілкою на відповідному ребрі графа, а саме таке орієнтоване ребро називають дугою. Якщо всі ребра графа орієнтовані за напрямом, то такий граф називають орієнтованим або, скорочено, орграфом. Зокрема, як орграф можна розглядати стандартні траєкторії зниження і заходження на посадку на конкретному аеродромі, повітряні траси для виконання польотів у східному або західному напрямах тощо.

Вершину і ребро (дугу) графа, що з’єднані між собою, називають інцидентними ребром (дугою) і вершиною.

Якщо на орграфі дуга “виходить з вершини”, то інцидентність таких дуги і вершини вважають позитивною, якщо ж дуга входить у вершину, то таку інцидентність вважають від’ємною. Означаючи “0” відсутність інцидентності, “+1” і ”-1” позитивну і негативну інцидентність відповідно, записують орграф у вигляді матриці.

Орграфи, які розрізняються тільки схематичним зображенням, але ідентичні за інцидентністю їх вершин і дуг, називають ізоморфними. Приклад таких графів показаний на рис. 6.2.

Ступенем вершини називають кількість дуг, що з’єднані з даною вершиною.

Паралельними називають дуги, що з’єднують одні й ті ж дві вершини.

Зваженим або розміченим називають граф, вершини і дуги (ребра) якого характеризуються певними числами. Зокрема, у вигляді графа можна розглядати мережу аеродромів (вершини) і повітряних трас (дуги), що їх з’єднують. При цьому “вагами ” аеродромів і повітряних трас можуть бути їх пропускні спроможності, в іншому випадку як ваги окремих ділянок повітряних трас можуть розглядатися їх протяжності, а як ваги вершин-аеродромів – обсяги перевезень, які необхідно виконати з відповідного аеродрому на інші, і т. п. Отже, при розв’язанні задач практичної діяльності фізичне значення ваг дуг і вершин однієї і тієї ж системи, що розглядається як граф, може бути різним в залежності від змісту і мети розв’язування задачі.

Рис. 6.2

У зваженому графі розрізнюють полюсні характеристики і характеристики зв’язків, до полюсних відносять характеристики вершин, а до характеристик зв’язку – “ваги” дуг графа.

Суміжними називають дві вершини графа, які є граничними вершинами одного й того ж ребра (однієї і тієї ж дуги).

Граф, який можна зобразити на площині без перетину його ребер (дуг), називають планарним.

Орієнтованим маршрутом на орграфі називають таку послідовність дуг, в якій кінцева вершина кожної попередньої дуги є початковою вершиною наступної дуги. Інакше кажучи, рух на такому маршруті відповідає напряму дуг орграфа. Маршрут, в якому нема дуг, що повторюються, називають шляхом, а маршрут, в якому також не повторюється ні одна вершина, називають простим шляхом.

6.3 Транспортні мережі

Транспортною мережею називають орграф, що має вхідну і вихідну вершини (вхід и вихід), яким властиві такі особливості: з вхідної вершини дуги виходять і ні одна дуга в неї не входить; у вихідну вершину дуги входять, ні одна дуга з неї не виходить. Приклад транспортної мережі показаний на рис. 5.3.

К ожна дуга транспортної мережі характеризується пропускною спроможністю, яка означається, як правило, цілим числом, що записується біля відповідної дуги. Пропускна спроможність дуги є її постійною характеристикою ( параметром ). Зокрема, як транспортну мережу можна розглядати ряд аеродромів ( вершини мережі ) і повітряні траси, встановлені маршрути ( дуги мережі ), що їх з’єднують і забезпечують польоти у східному або у західному напрямах. При цьому пропускною спроможністю кожної дуги мережі є допустима інтенсивність польотів на ешелонах, що з’єднують відповідні два аеродроми.

Кожну дугу мережі характеризують також фактичним потоком на ній, який не може бути більше пропускної спроможності дуги. Так, фактична інтенсивність польотів на повітряній трасі не може бути більше допустимої, тобто її пропускної спроможності.

Якщо фактичний потік дуги дорівнює її пропускній спроможності, то таку дугу називають насиченою.

Для будь-якої вершини мережі, крім її входу і виходу, дійсне правило збереження фактичного потоку: сума потоків дуг, що виходять з вершини, дорівнює сумі потоків дуг, що входять в дану вершину.

Сумарний фактичний потік між входом і виходом мережі називають потоком в мережі. Потік у мережі дорівнює сумі потоків вхідних дуг, що виходять з вершини - входу мережі, а також сумі потоків вихідних дуг, тобто дуг, що входять у вершину – вихід мережі.

Якщо мережа поділена на дві частини так, що до однієї з них відноситься вхід, а до іншої – вихід, то говорять, що на мережі здійснено переріз або що до мережі прикладено переріз. На рис. 6.3 лінія перерізу мережі показана пунктиром. Величиною перерізу називають суму пропускних спроможностей дуг, які перетинаються лінією перерізу. На рис. 6.3 показаний переріз, величина якого складає 15 одиниць.

Основна теорема теорії мереж встановлює наступне: пропускна спроможність мережі не може бути більше величини будь-якого її перерізу. Звідси випливає, що коли величина перерізу дорівнює пропускній спроможності мережі, то така величина перерізу є найменшою можливою у даній мережі. Наслідком згаданої теореми є також наступне: фактичний потік у мережі не може бути більше величини будь-якого її перерізу. Отже, переріз найменшої величини у мережі є її “вузьким місцем”, тобто для збільшення пропускної спроможності мережі необхідно збільшити пропускну спроможність дуг такого перерізу.

6.4 Алгоритм визначення пропускної спроможності мережі

Вважають, що транспортна мережа задана, якщо маємо її зображення у вигляді орграфа або відома матриця інцидентностей її вершин і дуг, а також відомі пропускні спроможності всіх дуг мережі. За цих умов можна визначити пропускну спроможність мережі, тобто максимальний можливий потік в ній. Алгоритм такого визначення полягає у наступному.

Послідовно переглядаючи кожний шлях між входом і виходом мережі і враховуючи результати всіх попередніх таких переглядів, визначають максимальний можливий потік на такому шляху. При цьому біля кожної дуги мережі записують сумарний потік в ній, одержаний при перегляді всіх шляхів мережі. Зрозуміло, що такий потік не може перевищувати пропускної спроможності дуги.

Після перегляду всіх можливих шляхів мережі її пропускну спроможність визначають як суму потоків вхідних або вихідних дуг мережі.

Р озглянемо приклад визначення пропускної спроможності мережі. Що зображена на рис. 6.4. При цьому пропускні спроможності дуг запишемо біля них без дужок, а визначений потік – в дужках.

1. Пропускна спроможність шляху “Вх. – А – Вих.” обмежена пропускною спроможністю дуги “A – Вих.“ і складе 4, потік, що дорівнює їй, записуємо вивести дужках біля дуг “Вх. - А” і “А – Вих.”.

2. Пропускна спроможність шляху “Вх. – В – А – Вих.” з врахуванням раніше записаних потоків дуг дорівнює нулю, оскільки дуга “А – Вих.” Цього шляху насичена. Відповідний потік (0) записуємо біля дуг цього шляху “Вх. – Вывести” і “В – А”.

3. Пропускна спроможність шляху “Вх. – В –Вих.” обмежується пропускною спроможністю дуги “В – Вих.” і дорівнює 5. Цей потік записуємо біля відповідних дуг. Закресливши при цьому потік “0”, що раніше був записаний біля дуги “Вх. – В”.

4. Пропускна спроможність шляху “Вх. – В – С – Вих.” (з врахуванням потоку 5 одиниць, що вже записаний біля дуги “Вх. – В”) складає 3 одиниці, тобто обмежена пропускною спроможністю дуги “Вх. – В”, тому записуємо такі потоки біля дуг цього шляху : “Вх. – В” – (8), закресливши записаний раніше потік (5) ; “В – С” - (3) ; “С – Вих.” – (3).

Далі визначаємо пропускну спроможність мережі як суму потоків на її вхідних дугах (4 + 8 = 12) або як суму потоків на її вихідних дугах (4 + 5 + 3 = 12).

Аналізуючи результати визначення пропускної спроможності даної мережі, робимо висновок, що її можна збільшити шляхом збільшення пропускної спроможності дуги “Вх. – В” або пропускної спроможності дуги “A – Вих.”, можливі також інші варіанти збільшення пропускної спроможності мережі. Разом з тим при даній конфігурації і параметрах (пропускних спроможностях її дуг) мережі дуга “В – А” не впливає на її пропускну спроможність.

6.5 Основні відомості про мережеве планування

Мережевий план (графік) складають у процесі підготовки до виконання складної роботи, яку можна представити як таку, що складається з ряду більш простих робіт, частина яких можуть виконуватися одночасно (“паралельно“), а інша частина – послідовно у часі, тобто одна після виконання іншої (інших). Наприклад, можна скласти мережевий графік виконання будівельних робіт або підготовки повітряного судна до вильоту тощо. В останньому графіку судно готується до вильоту послідовно інженерно-авіаційною службою, службою паливно-мастильних матеріалів, службою перевезень. А в цей же час, тобто “паралельно”, екіпаж судна проходить передполітну підготовку, після чого також готує судно до вильоту.

Основною метою складання мережевого графіка є мінімізація часу виконання роботи, що планується. Крім того, при виконанні деяких, наприклад, будівельних робіт такий графік використовують з метою мінімізації вартості їх виконання.

Мережевий графік за формою аналогічний транспортній мережі, але на ньому дугами означають “прості” роботи, що є складовими планованої, а вагою кожної дуги є час виконання відповідної простої роботи. Склавши такий графік, шляхом перегляду всіх можливих шляхів від його входу до виходу визначають шлях найбільшої “довжини”, тобто таку сукупність послідовно виконуваних робіт, яка потребує найбільшого часу. Такий шлях називають критичним. Наприклад, якщо мережу, яка зображена на рис. 6.2, вважати графіком, то на ньому критичним буде шлях “Вх. – В – С – Вих.“, “довжина” якого складає 16 одиниць. Зрозуміло, що час виконання всієї складної роботи можна зменшити, тільки зменшивши “довжину” критичного шляху, тобто час виконання хоча б частини робіт, що відображаються дугами цього шляху. Але усунувши один критичний шлях, прийдемо до того, що таким стане інший, більш короткий шлях. Отже, таке “зменшення довжини критичного шляху” можна продовжити до нескінченності. Але у процесі такого “ скорочення” враховують вартість с виконання кожної “простої“ роботи, яка, як правило, залежить від часу t її виконання так, як це показано на рис. 6.5.

З цього рисунка випливає, що існує оптимальний час виконання кожної роботи, при якому забезпечується мінімум її вартості. Тому у процесі удосконалення мережевого графіка, тобто скорочення критичного шляху, зменшують час виконання тих простих робіт такого шляху, вартість яких в результаті цього також зменшується. Крім того, при цьому діють відповідно до наступного правила: на критичному шляху скорочують, в першу чергу час виконання такої роботи, для якої похідна її вартості за часом має максимальне значення порівняно з такими ж похідними інших робіт цього ж критичного шляху. Це забезпечує найбільший виграш вартості робіт шляху при зменшенні часу їх виконання на одне і те ж значення.

Очевидно, ідеальним був би мережевий план (графік), на якому протяжності всіх паралельних шляхів між входом і виходом були б рівні між собою. Але здебільшого цього досягти не вдається, тому для формального збільшення протяжності частини шляхів іноді вводять фіктивні роботи, завдяки чому одержують такий “ ідеальний ” план.

Запитання для самоконтролю

1. Наведіть загальне означення графа.

2. З якою метою використовують графи у процесі розв’язування задач обслуговування повітряного руху?

3. Наведіть порядок розв’язування методами теорії графів задачі визначення оптимальної за протяжністю або вартістю лінії комунікації, що з’єднує кілька пунктів.

4. Наведіть означення орграфа і приклади орграфів в системі обслуговування повітряного руху.

5. Поясніть поняття “інцидентність дуг і вершин графа”, “зважений (розмічений) граф”.

6. Наведіть означення понять “орієнтований маршрут на орграфі”, “шлях і простий шлях на графі”.

7. Наведіть означення транспортної мережі як орграфа.

8. Яким може бути співвідношення між пропускною спроможністю дуги транспортної мережі і фактичним потоком тієї ж дуги? Сформулюйте правило збереження потоку для вершини мережі (крім вершин “вхід” і “вихід”).

9. Наведіть означення перерізу на мережі і величини перерізу.

10. Які співвідношення між величиною перерізу на мережі і її пропускною спроможністю можливі?

11. Наведіть послідовність і приклад визначення пропускної спроможності мережі.

12. Коли (при виконанні яких робіт) здійснюють мережеве планування? Які величини є вагами дуг мережевого графіку?

13. З якою метою здійснюють мережеве планування?

14. Який шлях на мережевому графіку називають критичним і як він впливає на загальний термін виконання планованої роботи?

15. Як залежить, як правило, вартість роботи від терміну її виконання? Як враховують цю залежність при скороченні критичного шляху мережевого графіку?