4.2 Забезпечення надійності систем шляхом резервування їх складових

У процесі аналізу функціонування навіть такої складової служби обслуговування повітряного руху як окремий диспетчерський пункт його, як правило, розглядають як складну ергатичну систему. А будь-яка складна система складається з підсистем і елементів, які пов’язані між собою. При цьому зв’язки між ними можуть бути більш-менш складними, а надійність всієї системи залежить не тільки від надійності її складових, а й від того, як вони з’єднані між собою.

В теорії надійності розрізняють послідовне, паралельне і змішане з’єднання підсистем (елементів) в системі. З’єднання складових системи вважають послідовним, коли відмова будь-якої з них призводить до відмови всієї системи. Приклад схематичного зображення такого з’єднання показаний на рис. 4.1,а , де складові системи означені 1, 2, ..., n.

В теорії ймовірностей розрізняють залежні і незалежні події. Незалежними вважають події, ймовірність однієї з яких не залежить від ймовірності іншої. Якщо послідовно з’єднані n об’єктів ( див. рис. 4.1,а ), ймовірності Р1с, Р2с, …, Рnс справного стану яких незалежні, то ймовірність справного стану такої системи :

Це випливає з означення ймовірності стану як відносного часу, протягом якого система перебуває у даному стані.

Тоді ймовірність несправного стану такої системи :

де Рiн - ймовірність несправного стану і-го елемента з’єднання.

Для випадку n=2 остання рівність приймає таку форму :

Як випливає з викладеного, у випадку послідовного з’єднання складових ймовірність справного стану системи не може бути більше ймовірності справного стану будь-якої її складової. Але не зважаючи на такий “недолік” послідовного з’єднання складових, воно досить часто зустрічається, в тому числі – в системі обслуговування повітряного руху. Зокрема, послідовно з’єднаний будь-який радіотехнічний засіб управління повітряним рухом і його джерело електроживлення, в системі радіозв’язку диспетчера управління повітряним рухом і екіпажу повітряного судна слід вважати, що вони послідовно з’єднані не тільки між собою, а й з технічними засобами, які при цьому використовуються на землі і на повітряному судні, і з повітряним простором, в якому розповсюджується радіосигнали. Разом з тим в останньому прикладі диспетчер і екіпаж у деяких випадках можуть оцінити правильність інформації, яку повідомляє один з абонентів іншому, тобто абоненти в деякій мірі “підстраховують”, “резервують” один одного. Наприклад, при наявності засобів радіолокаційного контролю диспетчер в зоні його відповідальності визначає положення повітряного судна відносно лінії заданого шляху і виявить помилку у повідомленні екіпажу судна. Така і інша подібна “підстраховка” однією підсистемою іншої є елементом резервування, що властиво підсистемам, які включені між собою паралельно. Взагалі кажучи, в авіації у більшості випадків діяльність будь-якого члена екіпажу повітряного судна в певній мірі контролюється іншими членами екіпажу, що можна вважати резервуванням. Це ж можна віднести до діяльності диспетчерів процедурного і радіолокаційного контролю тощо.

У тому випадку, коли система, яка складається з певної кількості підсистем (елементів), справна за умови справного стану хоча б однієї її підсистеми (елемента), вважають, що підсистеми (елементи) з’єднані між собою паралельно (рис. 4.1,б). Тому паралельне з’єднання елементів в системі звичайно розглядають як резервування одних таких елементів іншими. Зокрема, в системі управління повітряним рухом паралельно з’єднаними між собою є основна і резервна радіостанції зв’язку, основне, резервне і аварійне джерела електроживлення тих же радіостанцій, основний і резервний аеродроми тощо.

Очевидно, при паралельному з’єднанні n елементів, ймовірності справного (несправного) стану яких незалежні, ймовірність відмови системи (несправного стану всіх її елементів) :

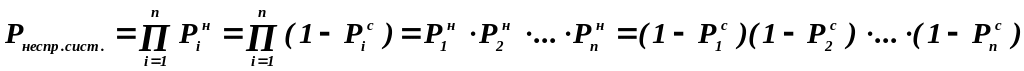
де Рiн - ймовірність несправного стану і-го елемента ; Рiс - ймовірність справного стану і-го елемента.

Зокрема, якщо n=2, то :

,

,

де Рспр.сист.- ймовірність справного стану системи.

Оскільки Р1с<1, Р2с<1, то Р1сР2с<Р1с, Р1сР2с<Р2с і на підставі останньої рівності робимо висновок, що ймовірність справного стану системи паралельно з’єднаних елементів не може бути меншою від ймовірності справного стану будь-якого з таких елементів. Отже, якщо передбачена “паралельна робота” технічних засобів або різних службових осіб, то вона має за мету підвищення надійності системи, що забезпечується тільки за умови виконання своїх функцій у повному обсязі кожним з елементів системи.

В теорії систем доказано, що паралельне з’єднання, тобто резервування, є економічно вигідним на рівні елементів – найпростіших складових системи. Разом з тим підсистеми в системах вигідно з’єднувати послідовно.

Схема змішаного з’єднання об’єктів в системі може мати різні конфігурації. Зокрема, на рис. 3.1,б відображена схема, в котрій елементами 1,2 і 3 можуть бути основне, резервне і аварійне джерела електроживлення, а елементами 4 і 5 – основна і резервна радіостанції зв’язку і т. п.