2. Уравнение и изотермы Ван-дер-Ваальса. Внутренняя энергия реального газа.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, галандский физик Ван-дер-Ваальс вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона-Менделеева введены две поправки.

1) Учет собственного объема молекул, наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактически свободный объем, в котором может двигаться молекула реального газа, будет не V_m, а V_m – b, где b – объем, занимаемый собственными молекулами. Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находится две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние меньше диаметра молекул. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т.е. объем равный восьми объемам молекул, или учетверенному объему молекулы в расчете на одну молекулу.

2) Действие сил притяжения газа приводит к появлению давления на газ, называемого внутренним давлением.

По вычислениям Ван-дер-Ваальса внутреннее давление обратно пропорционально квадрату молярного объема:

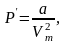
где a – постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа, или уравнение состояния реальных газов:

Для произвольного количества вещества газа получим:

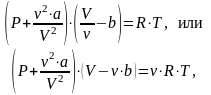
где a и b – постоянные для данного газа величины, определяемые опытным путем. Для этого записывается уравнение Ван-дер-Ваальса для двух известных состояний газа и система решается относительно a и b.

При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно тоже является весьма приближенным, хотя и лучше, особенно для сильно сжатых газов, согласуется с опытами, чем уравнение состояния идеального газа.

Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – это кривые зависимости P от Vm при заданных температурах. Эти кривые рассматриваются для четырех различных температур.

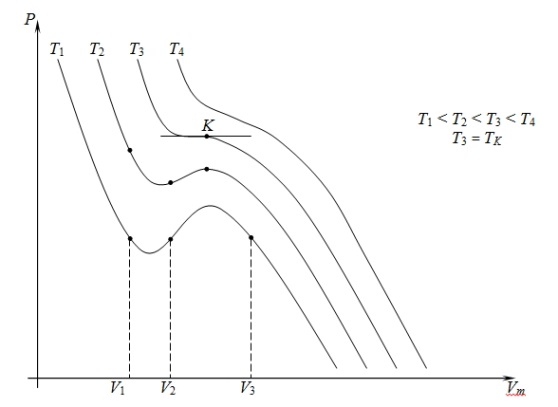
При высоких температурах, больших, чем T_K, изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы. При некоторой температуре T_K имеется лишь одна точка перегиба K. Эта изотерма называется критической, соответствующая ей температура T_K – критической температурой, точка перегиба K – критической точкой, в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке параметры V_K и T_K тоже называются критическими. Состояние с критическими параметрами P_K, V_K и T_K называется критическим состоянием.

Для исследования характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду:

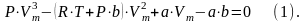
Это уравнение при заданных P и T является уравнением третьей степени относительно V_m, следовательно оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни, поэтому первому случаю соответствует изотерма при низких температурах, второму случаю – изотерма при высоких температурах.

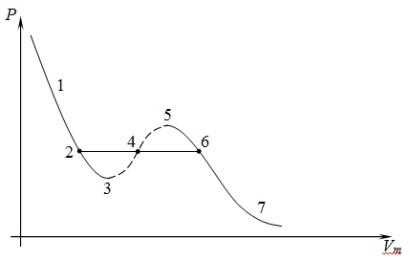
Рассматривая различные участки изотерм при T < T_K, видим, что на участках 1-3 и 5-7 при уменьшении объема давление возрастает, что является естественным. На участке 3-5 сжатие вещества приводит к уменьшению давления. Практика показывает, что такие состояния в природе не существуют. Наличие участка 3-5 означает, что при постоянном изменении объема вещество не может оставаться все время в виде одной среды. В некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7-6-2-1. Часть 6-7 отвечает газообразному состоянию, часть 2-1 – жидкому. В состоянии 6-2 наблюдается равновесие жидкой и газообразной фаз вещества.

Вещество в газообразном состоянии при температурах меньших T_K называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Для нахождения критических параметров подставим их в уравнение (1)

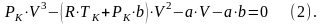
(индекс m для простоты опускаем)

Т.к. в критической точке все три корня совпадают и равны V_K, то уравнение можно привести к виду:

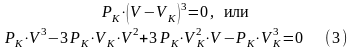
Т.к. уравнения (2) и (3) тождественны, следовательно в них равны коэффициенты при неизвестных соответствующих степеней, т.е.

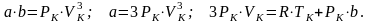
Решая их, получим коэффициенты:

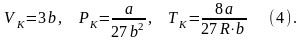
Проведем через крайние точки горизонтальных участков семейство изотерм – кривую AKM.

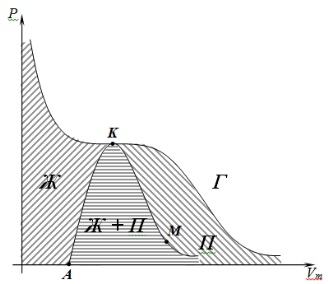
Эта кривая и критическая изотерма делят диаграмму PV под изотермой на области: Ж – область жидкого состояния, Ж + П – область двух фазных состояний (жидкость и насыщенный пар), П – область пара, Г – область газа.

Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ при температуре выше критической не может быть превращен в жидкость ни при каком давлении.

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул, которая определяет внутреннюю энергию идеального газа и потенциальную энергию межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ

Работа, которая затрачивается на преодоление сил притяжения, действующих между молекулами газа, идет на увеличение потенциальной энергии системы.

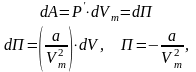
где постоянная интегрирования принята равной нулю. Знак «–» означает, что молекулярные силы, создающие внутреннее давление P, являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа

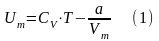
растет с повышением температуры и увеличением объема. Если газ расширяется без теплообмена с окружающей средой, т.е. dQ = 0, и не совершает внешней работы, т.е. dA = 0, то на основании первого начала термодинамики получим, что

U₁ = U₂ (2).

Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется. Равенство (2) формально справедливо как для идеального, так и для реального газа, но физический смысл для обоих случаев совершенно различен.

Для идеального газа равенство (2) означает равенство температур, т.е. T₁ = T₂, и при адиабатическом расширении идеального газа в вакуум его температура не изменяется.

Для реального газа из равенства (2) для моля газа

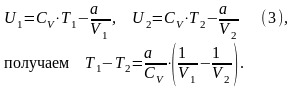
Т.к. V₂ > V₁, то T₁ > T₂, т.е. газ при адиабатическом расширении в вакуум охлаждается и наоборот, при адиабатическом сжатии в вакуум реальный газ нагревается.

3. На пластинах плоского конденсатора равномерно распределен за-ряд с поверхностной плотностью  = 0,2 мкКл/м2. Расстояние между пластинами 1 мм. На сколько изменится разность потенци-алов, если расстояние увеличить до 3 мм.