Билет №10

1.Применение I начала термодинамики к адиабатическому процессу.

Адиабатический процесс - это процесс, при котором отсутствует теплообмен с окружающей средой, следовательно, dQ = 0. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, процесс распространения звука в среде. Скорость распространения звука настолько велика, что процесс обмена энергией между звуковой волной и средой произойти не успевает и т.д. и т.п.

Из I начала термодинамики получают, что dA = –dU, т.к. dQ = 0, т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Для произвольной массы газа имеем:

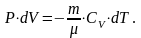
Если продифференцировать уравнение Менделеева-Клапейрона, то получим

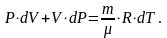
Исключив T, получим

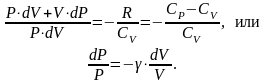
Интегрирую обе части от P₁ до P₂ и от V₁ до V₂, получим

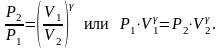
Т.к. состояния 1 и 2 выбраны произвольно, то можно записать, что

PV ^ = const.

Полученный результат есть уравнение адиабатического процесса, или уравнение Пуассона. Перейдя к переменным T и V или к переменным P и T, используя уравнение Менделеева-Клапейрона, получим

TV ^–1 = const; T ^P ^1– = const.

Эти формулы тоже выражают уравнение Пуассона, только в других параметрах.

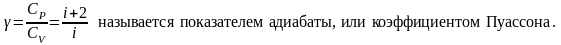
Для одноатомных газов i = 3,  = 1,67; для двухатомных газов i = 5,  = 1,4.

Значение , вычисленное по формуле, хорошо подтверждается экспериментом.

Диаграмма адиабатического процесса изображается гиперболой.

Вычислим работу, совершаемую газом в адиабатическом процессе. Если газ адиабатически расширяется от V₁ до V₂, то его температура уменьшается от T₁ до T₂.

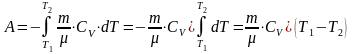
Произведя некоторые преобразования, можно перейти к виду

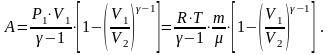
Работа, совершаемая газом при адиабатическом расширении, меньше, чем при изотермическом. Это можно объяснить тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянно за счет притока извне эквивалентного количества теплоты.

Рассмотренные процессы имеют общую особенность – они проходят при постоянной теплоемкости; в первых двух процессах они соответственно равны C_V и C_P. При изотермическом процессе dt = 0, теплоемкость равна . В адиабатическом процессе dQ = 0, следовательно, теплоемкость тоже равна нулю.

Процесс, при котором теплоемкость остается постоянной, называется политропным.

Исходя из I начала термодинамики, при условии, что теплоемкость постоянна, выводится уравнение политропы:

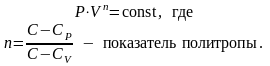
Очевидно, что при C = 0 n = , получаем уравнение адиабаты. При C =  n = 1, получаем уравнение изотермы. При C = C_P n = 0, получаем уравнение изобары. При C = C_V n = , получаем уравнение изохоры. Таким образом, все процессы являются частным образом от изотропного процесса.

2. Электрическое поле. Напряженность поля. Расчет полей методом суперпозиции.

Взаимодействие между зарядами осуществляется через электрическое поле. Электрическое поле покоящихся зарядов называется электростатическим. Электростатическое поле отдельного заряда можно обнаружить, если внести в это поле другой заряд, на который в соответствии с законом Кулона будет действовать определенная сила. Внесем в электрическое поле, созданное зарядом q, точечный положительный заряд, называемый пробным   . На этот заряд, по закону Кулона, будет действовать сила

Если в одну и туже точку помещать разные пробные заряды   ,   и т.д., то на них будут действовать различные силы, пропорциональные этим зарядам. Отношение   для всех зарядов, вносимых в поле, будет одинаковым и будет зависеть лишь от q и r, определяющих электрическое поле в данной точке. Эта величина является силовой характеристикой электрического поля и называется напряженностью (E). Итак

,

т.е. напряженность данной точки электрического поля это сила действующая на единичный положительный заряд, помещенный в эту точку.

Учитывая закон Кулона нетрудно получить выражение для напряженности поля создаваемого точечным зарядом q

или в векторной форме

За единицу напряженности принимается напряженность в такой точке поля, в которой на единицу заряда действует единица силы.

Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.

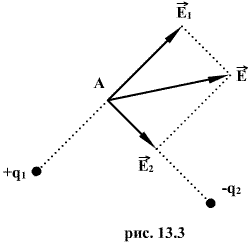
Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке А поля двух точечных зарядов   и   (рис. 13.1). Сложение векторов   и   производится по правилу параллелограмма. Направление результирующего вектора   находится построением, а его абсолютная величина может быть подсчитана по формуле

3. Под действием постоянной силы в 10Н тело движется прямолинейно так, что зависимость расстояния от времени дается уравнением S =А – Вt + Сt2 (А=5 м, В = 2 м/с, С = 1 м/с2) . Найти массу тела.