8.4. Соединение фаз нагрузки треугольником

С

а

оставим расчётную схему при соединении нагрузки треугольником (рис.8.17). При этом:

İ

Z_са

Z_аb

_A, İ_В, İ_С – линейные токи нагрузки, А;

İ

_aв, İ_bc, İ_ca – фазные токи нагрузки, А;

Рис.8.17

b

с

Z_bс

, , – линейные (фазные) напряжения нагрузки, В.

Как видно из расчётной схемы, фазное напряжение нагрузки равно линейному напряжению нагрузки, т.е.

Uф = Uл .

(8.40)

По первому закону Кирхгофа найдём линейные токи через фазные:

İА = İab – İca ;	(8.41)
İВ = İbc – İab ;	(8.42)
İС = İca – İbc .	(8.43)

Построим векторную диаграмму линейных напряжений, фазных и линейных токов на комплексной плоскости (рис.8.18).

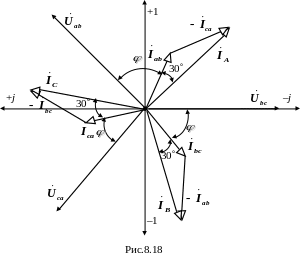
Установим связь между действующими значениями фазных и линейных токов нагрузки при соединении её фаз треугольником, для чего рассмотрим треуголь­ник токов (рис.8.19).

Из треугольника токов находим:

Iл = 2 Iф cos 30° = 2 Iф = Iф .

(8.44)

8.5. Расчёт неразветвлённых трёхфазных цепей синусоидального тока

Рассмотрим расчётную схему четырёхпроводной трёхфазной системы (рис.8.20), в которой известны сопротивления: z_A = z_B = z_C, z_лА = z_лВ = z_лС, z_N, z_a = z_b = z_c, а также действующее значение фазной э.д.с. E. Необходимо определить токи и напряжения: İ_А, İ_В, İ_С, _лА, _лВ, _лС, _а, _в, _с, _ab, _bc, _ca, а также активную, реак­тивную и полную мощности нагрузки.

Пусть потенциал точки 0 равен нулю. Докажем, что потенциал точки 0' также равен нулю. Для этого согласно метода двух узлов запишем выражение для рас­чёта напряжения между точками 0' и 0, которое называется напряжением смеще­ния нейтрали ( _N):

,

(8.45)

где

.

Если в формуле (8.45) вынести за скобки комплексную проводимость, то в скобках останется алгеб­раическая сумма э.д.с, которая равна нулю. Поэтому на­пряжение смещения нейтрали также равно нулю, а это значит, что потенциал точки 0' равен нулю. Таким образом, при симметричном режиме точки 0 и 0' можно соединить, а это упрощает расчёт схемы, который сводится к расчёту од­ной фазы (например, фазы А), рис.8.21.

Сначала находим линейный (фазный) ток:

,

затем – падение напряжения в линии

,

а также фазное напряжение нагрузки

.

Для нахождения токов İ_В и İ_С, напряжений _b и _с, а также падений напряжений в линии _лВ и _лС необхо­димо ток İ_А, напряжение _а и падение напряжения _лА умножить соответственно на е^–j120° и е^–j240°. Линейные напряжения нагрузки можно найти как разность фазных напряжений:

ab = a – b ;
bc = b – c ;
ca = c – a .

Активная, реактивная и полная мощности, которые потребляет нагрузка:

P = 3 UфIф cos φ ;	(8.46)
Q = 3 UфIф sin φ ;	(8.47)
S = 3 UфIф .	(8.48)

где U_ф и I_ф – фазные соответственно напряжение и ток;

φ – угол сдвига фаз на­грузки.

Найдём мощности через линейные напряжение и ток. Для этого заменим фаз­ные напряжение и ток на линейные – , I_ф = I_л .

P = UлIл cos φ ;	(8.49)
Q = UлIл sin φ ;	(8.50)
S = UлIл .	(8.51)

Расчёт трёхпроводной трёхфазной системы при соединении генератора и на­грузки треугольником выполня­ется аналогично.

Рассмотрим расчётную схему трёхпроводной трёхфазной системы при соедине­нии генератора и нагрузки треугольником (рис.8.22), в которой известны сопро­тивления: z_AB = z_BC = z_CA, z_лА = z_лВ = z_лС,, z_ab = z_bc = z_ca, а также действующее значе­ние фазной э.д.с. E. Необходимо определить токи İ_А, İ_В, İ_С, напряжения _аb, _bc, _сa, падения напряжения в линии _лА, _лВ, _лС, токи İ_аb, İ_bc, İ_ca а также активную, реактивную и полную мощности нагрузки.

Для расчёта приведенной схемы необходимо сначала преобразовать схемы со­единения фаз генератора и нагрузки треугольником в эквивалентные схемы со­единения звездой (рис.8.23).

Находим эквивалентные э.д.с. и параметры:

;	(8.52)
;	(8.53)
.	(8.54)

Далее расчёт выполняется так, как указано ранее.

Фазные токи нагрузки находятся через линейные (фазные) напряжения на­грузки:

;	(8.55)
;	(8.56)
.	(8.57)

Расчёт трёхпроводных трёхфазных систем при соединении генератора звез­дой, а нагрузки треугольником, а также при соединении генератора треугольни­ком, а нагрузки звездой выполняем в такой последовательности. Сначала прово­дим эквивалентное преобразование схемы соединения генератора или нагрузки треугольником в эквивалентную схему соединения звездой, а потом выполняем расчёт так, как указано ранее.