7.1 Моделі поведінки виробника

7.2 Умови роботи двох фірм на ринку одного товару

7.1 Розглянемо математичну постановку задачі виробника.

Фірма випускає продукцію одного виду. Обсяг продукції, який випускається за конкретний період часу (наприклад, за рік, місяць тощо) позначимо Y. Обсяг продукції фірми визначається виробничою функцією. Передбачається, що ця функція безперервна та диференційована

де - обсяг витрат ресурсів або виробничих факторів.

До виробничих факторів можуть бути віднесені: основні виробничі фонди, трудові ресурси (середня чисельність зайнятих людей або відпрацьованих людино-днів за конкретний період часу), витрачені за цей проміжок часу матеріали, сировина, енергія тощо.

Нехай – вектор – рядок цін ресурсів, а p – ціна продукції. Тоді прибуток фірми дорівнює

Тут - доход фірми при випуску розглянутої продукції, - вартість витрат ресурсів за конкретний період часу.

Задача максимізації прибутку має вигляд

Для пошуку оптимальних значень вектору необхідно розглянути перші похідні

Цей вираз можна переписати таким чином

Прирівнюємо перші похідні нулеві

Перепишемо цей вираз у вигляді

Звідси

Тепер розглянемо модель, якщо фірма хоче максимізувати обсяг випуску продукції. До розглянутих умов додається така умова: відома вартість С витрат ресурсів за конкретний період часу, але невідома ціна одиниці продукції, що випускається. Цільову функцію та обмеження представимо у вигляді

Побудуємо функцію Лагранжа

тут – множник Лагранжа. Щоб максимізувати цю функцію необхідно розглянути перші похідні

Перепишемо останні рівняння у вигляді

Прирівнюємо ці похідні нулеві

Вирішуючи цю систему, можна знайти оптимальні значення вектору

7.2 Розглянемо ринок двох фірм, що випускають продукцію одного виду. Нехай собівартість випуску одиниці продукції дорівнює а. Зробленай обома фірмами продукція надходить на загальний ринок. Ціна на товар лінійно падає в залежності від загальної кількості товару, що надходить на ринок

x = x₁+x₂ ,

, ,

де х₁ – обсяг продукції першої фірми,

х₂ - обсяг продукції другої фірми,

с - гранично висока (максимальна) ціна продукції,

b – коефіцієнт лінійної залежності.

Прибуток першої фірми можна визначити по формулі:

,

де .

Прибуток другої фірми можна визначити по формулі:

.

Поведінка кожної фірми визначається її прагненням максимізувати вій прибуток. Допустимо, що перша фірма довідалася про стратегію другої фірми, тобто про її обсяг випуску продукції. Тоді перша фірма вибирає свій випуск з умови максимізації свого прибутку:

,

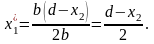
Друга фірма також вибирає свій випуск з умови максимізації свого прибутку:

,

, .

Тема 8

Моделювання співробітництва та конкуренції фірм

План

8.1 Стратегія Курно

8.2 Стратегія Стакельберга

8.3 Стратегія монополії

8.4 Стратегія картелю

8.1 Стратегія кожного підприємства визначається її прагненням максимізувати свій прибуток.

Відповідно стратегії Курно, припускаємо, що виробничі цикли підприємств збігаються. Тоді підприємства вибирають свої оптимальні випуски, знаючи обсяг виробництва свого конкурента за минулий або поточний періоди. Нехай .

Обсяг випуску за попередній період дорівнює:

.

Обсяг випуску за нинішній період дорівнює:

.

На підставі (2.8) і (2.9) знайдемо х₁ і х₂.

.

Обсяг випуску продукції другого підприємства дорівнює:

.

Ціна продукції визначається по формулі:

р(х) = с – bх = с - .

Прибуток підприємств дорівнює:

, .

Загальний прибуток двох підприємств:

.

Рисунок 8.1

8.2 Відповідно стратегії Стакельберга, припускаємо, що одне з підприємств свідомо розкриє свою стратегію. Нехай перше підприємство дасть можливість другому підприємству довідатися свій обсяг х₁, тоді друге підприємство випустить продукцію в обсязі: . Перше підприємство буде тепер діяти, виходячи саме з такої стратегії другого підприємства. Знайдемо прибуток першого підприємства:

.

З огляду на, що 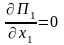знаходимо. .

Ціна продукції дорівнює:

р(х) = с – bх = с - .

Прибуток двох підприємств відповідно:

, .

Сумарний прибуток:

.

8.3 В умовах співробітництва двох підприємств можливе утворення монополії, що поєднує обоє підприємства в одне, і картелю, по суті являющегося таємною змовою двох учасників ринку з метою максимізації прибутку. Для монополії загальний прибуток буде дорівнює bd^2/4, а для картелю в загальному випадку прибуток кожного учасника буде рівної bd^2/8 при рівних обсягах випуску продукції

, , .

8.4 Картель – таємна змова декількох фірм із метою підтримки заданої ціни. Припустимо, що антимонопольне законодавство забороняє злиття двох фірм – утворення монополії .

Тому ці фірми використовують попередні розрахунки .кожна фірма буде випускати одиниць товару прибуток дорівнює ; ;

Результати розрахунків оформимо у виді табл.

Стратегія	х1	х2	х	П1	П2	П	р
Курно
Стакельберга
монополії
картелю

Висновки:

1. Для споживача найбільш краща крапка Стакельберга, у якій ціна товару min а обсяг випуску max .

2. Для споживача менш усього сприятливо ситуація монополії або Картелю, де ціна max , а випуск товару ­min ,а сумарний прибуток – max .

Тема 9

Рейтингове оцінювання та управління в економіці

План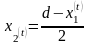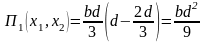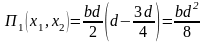