Міністерство освіти і науки України

Харківський національний університет радіоелектроніки

КОНСПЕКТ ЛЕКЦІЙ

з дисципліни

"МОДЕЛЮВАННЯ ЕКОНОМІКИ"

для студентів усіх форм навчання спеціальності "Економічна кібернетика"

Частина 1

Протокол № від «___»____2011

Затверджено кафедрою

“Економічна кібернетика”

Харків 2011

Конспект лекцій з дисципліни "Моделювання економіки" для студентів усіх форм навчання спеціальності "Економічна кібернетика". Частина 1 / Упоряд. Р.В. Петрова – Харків: ХНУРЕ, 2011.  50 с.

Упорядник Р.В. Петрова

ЗМІСТ

1. Вступна тема..............................................................................................4

1.1 Економіка як об’єкт моделювання......................................................4

1.2 Історія розвитку економіко-математичних методів та моделей.......5

2. Концептуальні засади математичного моделювання економіки...........8

2.1 Особливості математичного моделювання економіки.......................8

2.2 Класифікація економіко-математичних моделей................................8

2.3 Перевірка адекватності моделі............................................................10

2.4 Аналіз етапів економіко-математичного моделювання...................10

3. Дослідження економічних функцій.........................................................14

3.1. Функція витрат....................................................................................14

3.2 Функції попиту.....................................................................................15

3.3 Функції пропозиції...............................................................................16

3.4 Функція корисності споживача...........................................................18

4. Моделювання поведінки споживачів......................................................21

4.1 Модель поведінки споживача.............................................................21

4.2 Рівняння Є.Слуцького.........................................................................22

5. Моделі взаємодії споживачів та виробників..........................................24

5.1. Рівновага на ринку одного товару.....................................................24

5.2 Павутиноподібна модель ринку..........................................................24

5.3 Модель Еванса………………………………………………………..27

6. Виробничі функції та їх властивості.......................................................30

6.1 Види виробничих функцій..................................................................30

6.2 Граничний аналіз факторів..................................................................31

6.3 Однорідність виробничих функцій.....................................................31

6.4 Еластичність виробничих функцій.....................................................32

6.5 Заміна факторів у виробничих функціях...........................................33

6.6 Виробнича функція Кобба-Дугласа....................................................36

7. Моделювання поведінки виробників......................................................37

7.1 Моделі поведінки виробника..............................................................39

7.2 Умови роботи двох фірм на ринку одного товару............................41

8. Моделювання співробітництва та конкуренції фірм.............................43

8.1 Стратегія Курно....................................................................................43

8.2 Стратегія Курно....................................................................................44

8.3 Стратегія монополії..............................................................................45

8.4 Стратегія картелю.................................................................................45

9. Рейтингове оцінювання та управління в економіці...............................46

9.1 Концепція рейтингового управління..................................................46

9.2 Модель обчислення рейтингу економічної системи.........................47

10. Прикладні математичні моделі фінансово-економічних процесів.....49

10.1 Математичні моделі фінансових процесів.......................................49

10.2 Вибір інвестиційного проекту...........................................................50

Рекомендована література………………………………………………....51

Тема 1

ВСТУПНА ТЕМА

План

1.1 Предмет, суть та задачі дисципліни

1.2 Економіка як об’єкт моделювання

1.3 Історія розвитку економіко-математичних методів та моделей

1.1 Предметом дисципліни є методологія, методи і процеси економіко-математичного моделювання.

Сутність дисципліни - визначення внутрішніх закономірностей економічних процесів і явищ .

Метою дисципліни є формування системи знань по методології, методиці й інструментарію побудови економічних моделей, їхнього аналізу і використання.

До задач дисципліни відносяться вивчення теорії й одержання практичних навичок моделювання й аналізу економічних об'єктів і процесів на макро-, мезо- і мікроекономічних рівнях. Це можна зробити за допомогою моделей.

Методами, що їх використовують у моделюванні економіки (соціально-економічних систем), є синергетичний і системний аналіз економіки як складної нестабільної динамічної системи.

1.2 Об’єкт вивчення дисципліни «Моделювання економіки» — соціально-економічні системи, економіка та її підрозділи, окремі господарські одиниці, процеси, які в них відбуваються.

Основне призначення економіки — забезпечення суспільства предметами споживання та послугами, котрі створюють умови для життя та безпеки людини, родини, суспільства, країни. У зв’язку з цим є сенс розглядати, досліджувати та моделювати соціально-економічні системи.

Зазначимо, що під соціально-економічною системою мають на увазі складну ймовірнісну динамічну систему, що охоплює процеси виробництва, обміну, розподілу й споживання матеріальних та інших благ. Соціально-економічні системи належать до класу кібернетичних, тобто керованих, систем.

Економіка складається з елементів — господарських одиниць (підприємств, фірм, банків тощо). Надсистема економіки — природа та суспільство, дві її головні підсистеми — виробнича та фінансово-кредитна.

У процесі створення ВВП виробнича підсистема економіки виробляє та споживає проміжний продукт. За матеріально-речо­вим складом проміжний продукт — предмети праці — використовується в поточному виробничому споживанні, а його вартість переходить у вартість засобів праці чи предметів споживання, що входять до ВВП. На рис. 1.1 наведена схема процесів виробництва, розподілу, накопичення та споживання.

Проміжна продукція — це паливо, енергія, сировина, матеріали, комплектувальні вироби тощо. Зазначимо, що не існує абсолютно чіткої межі між проміжним продуктом і предметом споживання. Наприклад, цемент, проданий населенню, належить до предметів споживання, а цемент, закуплений будівельним підприємством, — до проміжної продукції.

Рис. 1.1 - Потоки продуктів і ресурсів в економіці

У сучасному суспільстві роль специфічного товару — загального товарного еквівалента — виконують гроші. Фінансово-кредитні установи (державні та комерційні банки, їхні філії, страхові компанії, різноманітні фонди тощо) спільно з фінансово-бухгалтерськими службами господарських комірок утворюють фінансово-кредитну підсистему економічної системи.

Використовуючи системний підхід щодо дослідження економіки на підставі математичних моделей, виокремлюють, зокрема, макро- та мікроекономічні моделі. Перші відображають функціонування та розвиток усієї економічної системи чи її великих підсистем, другі — господарських комірок та їх об’єднань.

1.3 Першу економічну модель в економіці сформулював у 1758 р. французький учений , придворний лікар Франсуа Кене . Кене довго міркував над розподілом у суспільстві праці і доходів. Він вичертив схему, що ввійшла в історію під назвою «Зиґзаґ доктора Кене» та «Арифметична формула» .

Дійсним першовідкривачем математичної економіки в Європі визнається французький економіст Антуан Огюстен Курно, що у 1838 році запропонував математичний апарат фірми, показав попит як падаючу функцію ціни. А.О. Курно написав книгу «Дослідження про математичні принципи теорії багатств ».

У 1847 році в Лозанні вийшла книга Леона Вальраса , у якій він писав

«Чиста теорія економіки є наука , що нагадує в усьому фізико-математичні науки». Леон Вальрас розробив теорію загальної конкурентної рівноваги і побудував узагальнену модель капіталістичної економіки.

Необхідно відзначити роботи з моделировапнию економіки В. Леонтьева, Дж. Фон Неймана, В. Парето, Е. Енгеля , Ф. Еджворта.

Василь Леонтьев ( 1906-1999 р.р. ) - американський економіст, російський по походженню. Основоположник напрямку, названого ним методом « витрати – випуск » або по вітчизняній термінології, методу міжгалузевого балансу . Одержав Нобелівську премію по економіці .

Дж. фон Нейман ( 1903 – 1957 р.р. ) - американський математик, виходець з Угорщини. Розробив логічні основи ЕОМ і автоматів , побудував разом з О. Моргенштерном теорію ігор . Відома його математична модель « економіки, що розширюється».

В. Парето ( 1848 – 1927 р.р. ) - італійський економіст і соціолог . У 1897 році він винайшов формулу, що блага розподіляються нерівномірно, розробив принцип багатоцільової «оптимальності ».

Німець Е. Енгель придумав теорії функцій попиту й еластичності показників .

Англієць Ф. Еджворт запропонував криві байдужності .

У кінці 19 століття в Європі та США одержали великий розвиток статистичні дослідження ( з нестатків астрономії для усунення помилок у спостереженнях ) і виник метод найменших квадратів, регресивний аналіз ( з нестатків біології ). Вони увійшли важливою складовою частиною в економетрію.

Серед вітчизняних учених, які внесли значний внесок у економіко-математичне моделювання необхідно назвати Є.Є. Слуцького, Л.В. Канторовича, В.С. Немчинова, М.П. Федоренко, Г.А. Аганбегяна .

У 1939 році здійснилася подія, яка спочатку ніким не було замічена , але потім відгукнулася в усім світі. Молодий професор Ленінградського університету Л.В. Канторович ( 1912 – 1986 р.р. ) надумав застосувати математичні прийоми до рішення виробничих задач. Такі задачі йому запропонував існуючий тоді Фанерний трест. Як розкроїти фанерні аркуші з мінімальними відходами, як розподілити роботу верстатів, щоб результати були максимальними? Результати були разючі. Математичний розрахунок пропонував єдиний найбільш ефективний варіант використання ресурсів.

У 1958 році майбутній академік В. С. Немчинов створив першу в країні економіко-математичну лабораторію. У 1963 р. на базі лабораторії В.С. Немчиновым був організований Центральний економіко-математичний інститут. Директором був призначений М. П. Федоренко, згодом академік. У Новосибірську був створений Інститут економіки й організації промислового виробництва АН СРСР, що очолив академік Г.А. Аганбегян.

Нижче наведені дані про вітчизняних учених, які внесли найбільший внесок у моделювання економіки.

Слуцький Євген Євгенович ( 1880–1948 р.р. ) - радянський математик , економіст і статистик, займався теорією попиту та споживання, вивів

«рівняння Слуцького» ( яке характеризує залежність між зміною цін на окремі товари і доходів споживачів з одного боку, та структурою попиту з іншої ).

Канторович Леонід Віталійович ( 1912–1986 р.р. ) - радянський математик і економіст, вніс вклад у розвиток ціноутворення, теорії ефективності капіталовкладень. Лауреат Нобелівську премії по економіці.

Немчинов Василь Сергійович ( 1894–1964 р.м. ) – основоположник економіко-математичного напрямку науки в країні, керував роботами зо міжгалузевих балансів країни і регіонів .

Аганбегян Абел Газевич ( родився в 1932 р. ), академік, основні праці з проблем продуктивності праці, галузевої оптимізації .

Федоренко Микола Прокофієвич ( родився в 1917 р. ), академік, радянський економіст, організатор і директор Центрального економіко-математичного інституту до 1985 року,займався проблемами застосування економіко-математичних методів у народному господарстві .

ТЕМА 2

Концептуальні засади математичного моделювання економіки

План

2.1 Особливості математичного моделювання економіки

2.2 Класифікація економіко-математичних моделей

2.3 Перевірка адекватності моделі

2.4 Аналіз етапів економіко-математичного моделювання

2.1 З давніх часів і дотепер для дослідження об'єктів, явищ і процесів використовується метод моделювання. Під моделюванням розуміється вивчення об'єктів дослідження не безпосередньо, а непрямим шляхом, за допомогою моделей.

Метод моделювання ґрунтується на принципі аналогії, тобто можливостях вивчення реального об’єкта не безпосередньо, а шляхом дослідження подібного йому й більш доступного цьому дослідженню об’єкта — його моделі. У подальшому йтиметься лише про економіко-математичне моделювання, тобто про опис соціально-економічних систем знаковими математичними засобами.

Практичними завданнями економіко-математичного моделювання є: по-перше, аналіз економічних об’єктів і процесів; по-друге, економічне прогнозування, передбачення розвитку економічних процесів; по-третє, вироблення управлінських рішень на всіх рівнях господарської ієрархії управління.

Зазначимо, що не в усіх випадках дані, отримані в результаті економіко-математичного моделювання, можуть використовуватися безпосередньо як готові управлінські рішення. Швидше всього вони можуть розглядатись як «консультуючі» засоби. Прийняття управлінських рішень залишається за людиною. Отже, економіко-математичне моделювання є лише однією з важливих компонент у людино-машинних системах аналізу, планування й управління економічними системами. Воно спрямоване на отримання нових знань про об’єкт дослідження.

2.2 Термін “модель” походить від латинського слова “modulus”, що означає “зразок”.

Моделлю деякої системи або об'єкта називається штучна система або об'єкт, що у визначених умовах можуть замінити оригінал шляхом відтворення його властивостей і характеристик.

Розрізняють моделі наступних видів

1. фізичні ( зовнішньої подоби ),

2. схематичні ( графічні ),

3. словесні ( вербальні ),

4. математичні.

Математичні моделі є найбільш абстрактними.

Математична модель – це модель, у якій для опису властивостей і характеристик об'єкта або процесу використовують математичні символи та методи. Сутність математичного моделювання полягає в заміні оригіналу його “образом” – математичною моделлю і подальшим дослідженням моделі.

В останній час широко використовуються економіко-математичні моделі. Під економіко-математичною моделлю розуміють концентроване вираження найсуттєвіших економічних взаємозвязків досліджуваних обєктів (процесів) у вигляді математичних функцій, нерівностей, рівнянь.

Розширимо це поняття. Економіко-математичними моделями назвемо математичні моделі, що використовуються для рішення задач та опису об’єктів і процесів економіки, менеджменту, маркетингу. Ці моделі можуть застосовуватися для аналізу об’єктів і процесів, їх прогнозування, вироблення управлінських рішень. Але результати моделювання є “консультуючими” засобами. Особа, яка приймає рішення, тобто менеджер приймає рішення про ступінь використання результатів моделювання.

Економіко-математичні моделі можна класифікувати за різними ознаками. Ці ознаки відносяться до цілей моделювання, особливостей обєктів, що розглядаються, та інструментарію побудови моделей. Розглянемо класифікацію економіко-математичних моделей.

Теоретичні моделі застосовуються для дослідження загальних властивостей процесів та явищ.

Прикладні моделі використовуються для рішення конкретних задач.

У макроекономічних моделях розглядають економіку як одне ціле. До макроекономічних моделей відносятья моделі народного господарства країни, галузей та регіонів.

До мікроекономічних моделей відносяться моделі фірм, підприємств та їх підрозділів.

У детермінованих моделях існують тільки жорстокі функціональні звязки між змінними.

В стохастичних моделях існують випадкові звязки між змінними.

Усі величини статичних моделей відносяться до одного моменту або періоду часу.

В динамічних моделях розглядаються залежності змінних у часі.

В оптимізаційних моделях вибирається найкращий варіант із визначеного числа варіантів виробництва, розподілу та споживання.

До експертних відносяться моделі, у яких через відсутність кількісних характеристик використовуються оцінки, виставлені експертами по визначеній шкалі.

У балансових моделях розглядаються вимоги відповідності наявності ресурсів і їхнього використання.

Важливу роль при розробці економіко-математичних моделей має поняття адекватності моделі, тобто її відповідність реальному процесові або явищу. Звичайно адекватність моделі (фізичної, схематичної тощо) перевіряють на практиці, але для економіко-математичних моделей така перевірка утруднена або вимагає значних витрат. Тому в економіко-математичному моделюванні використовують логічний аналіз або моделі, які добре себе зарекомендовали на практиці. До таких моделей можна віднести виробничі функції, моделі міжгалузевих балансів тощо.

2.3 Одним із важливих аспектів у економіко-математичному моделюванні, як і в інших концепціях моделювання, є поняття адекватності моделі, тобто відповідності моделі модельованому об’єк­тові чи процесові. Адекватність моделі — дещо умовне поняття, оскільки повної відповідності моделі реальному об’єктові не може бути. Це є характерним і для економіко-математичного моделювання. Йдеться не просто про адекватність, а про відповідність тим властивостям, які вважаються суттєвими для дослідника, відповідають меті дослідження та усталеній системі гіпотез. Зазначимо, що перевірка адекватності економіко-математичних моделей не є простою. Вона обтяжена складністю вимірювання економічних величин. Але без такої перевірки застосування результатів моделювання в аналізі та управлінських рішеннях може не лише виявитися малокорисним, а й призвести до негативних наслідків.

Звичайно адекватність моделі (фізичної, схематичної тощо) перевіряють на практиці, але для економіко-математичних моделей така перевірка утруднена або вимагає значних витрат. Тому в економіко-математичному моделюванні використовують логічний аналіз або моделі, які добре себе зарекомендовали на практиці. До таких моделей можна віднести виробничі функції, моделі міжгалузевих балансів тощо.

2.4 Процес економіко-математичного моделювання включає три структурних компоненти: суб’єкт дослідження або дослідника, об’єкт дослідження та модель. Обєктом дослідження можуть бути процеси та явища економіки, менеджменту, маркетингу, окремі господарські одиниці тощо. Дослідник вивчає основні структурні та функціональні характеристики об’єкта дослідження і розробляє модель. Для одного об’єкта дослідження може бути побудовано декілька моделей, які характеризують об’єкт з різних боків. Далі на основі використання результатів функціонування моделі дослідник робить висновки про об’єкт дослідження. Процес моделювання є циклічним процесом, бо знання про об’єкт дослідження розширюються та поглиблюються, а модель поступово удосконалюється.

У методології моделювання, таким чином, закладені можливості саморозвитку.

Основні етапи процесу моделювання розглядалися вище. Зауважимо, що в різних галузях знань, зокрема в економіці, вони набувають специфічних рис. Проаналізуймо послідовність і зміст етапів одного циклу економіко-математичного моделювання.

1. Постановка економічної проблеми та її якісний аналіз. Головне тут — чітко сформулювати сутність проблеми (цілі дослідження), припущення, які приймаються, і ті питання, на які необхідно одержати відповіді. Цей етап включає виокремлення найважливіших рис і властивостей об’єкта, що моделюється, і абстрагуван­ня від другорядних; вивчення структури об’єкта і головних залежностей, що поєднують його елементи; формулювання гіпотез (хоча б попередніх), що пояснюють поведінку і розвиток об’єкта.

2. Побудова математичних моделей. Це — етап формалізації економічної проблеми, вираження її у вигляді конкретних математичних залежностей і відношень (функцій, рівнянь, нерівностей тощо). Спочатку зазвичай визначається основна конструкція (тип) математичної моделі, а потім уточнюються деталі цієї конструкції (конкретний перелік змінних і параметрів, форма зв’язків). Таким чином, побудова моделі має кілька стадій. Неправильно думати, що чим більше чинників ураховує модель, тим краще вона «працює» і ліпші дає результати. Те саме можна сказати й про такі характеристики складності моделі, як використовувані форми математичних залежностей (лінійні та нелінійні), урахування чинників випадковості й невизначеності тощо. Надмірна складність і деталізованість моделі утруднює процес дослідження. Тре­ба не лише враховувати реальні можливості інформаційного і математичного забезпечення, а й порівнювати витрати на моделювання з одержуваним ефектом (зі зростанням складності моделі приріст витрат може перевищити приріст ефекту). Однією з важливих особливостей математичних моделей є потенційна можливість їх використання для вирішення різноманітних проблем. Тому, навіть зустрічаючись з новою економічною задачею, не треба намагатися «винаходити» модель; спочатку необхідно спробувати застосувати для розв’язання цієї задачі вже відомі моделі (адаптувати їх до задачі).

У процесі побудови моделі здійснюється зіставлення двох систем наукових знань — економічних і математичних. Звичайно, треба прагнути того, щоб одержати модель, яка належить до добре вивченого класу математичних задач. Часто це вдається зробити шляхом деякого спрощення вихідних положень моделі, які не спотворюють суттєві риси модельованого об’єкта. Однак можлива й така ситуація, коли формалізація економічної проблеми приводить до невідомої раніше математичної структури. Проблеми економічної науки і практики в середині ХХ ст. сприяли розвиткові математичного програмування, теорії гри, функціонального аналізу, обчислювальної математики. Цілком імовірно, що в майбутньому розвиток економічної науки стане важливим стимулом для створення нових розділів математики.

3. Математичний аналіз моделі. Метою цього етапу є з’ясу­вання загальних властивостей моделі. Тут часто застосовують математичні прийоми дослідження. Найважливіший момент — доведення існування рішень у сформованій моделі (теорема існування). Якщо поталанить довести, що математична задача не має рішення, то необхідність у наступній роботі за первісним варіантом моделі відпадає; слід скоригувати чи постановку економічної задачі, чи модифікувати її математичну формалізацію. В аналітич­ному дослідженні моделі можуть постати такі питання, як, наприклад: чи взагалі є та чи єдине рішення; які змінні (невідомі) можуть входити у рішення; які будуть співвідношення між ними; в яких межах і залежно від яких вихідних умов вони змінюються; якими є тенденції цих змін тощо. Аналітичне дослідження моделі порівняно з емпіричним (числовим) має ту перевагу, що одержувані висновки зберігають свою силу за різноманітних конкретних значень зовнішніх і внутрішніх параметрів моделі. Знання загальних властивостей моделі має настільки велике значення, що часто задля доведення подібних властивостей дослідники свідомо йдуть на ідеалізацію первинної моделі. І все-таки моделі складних економічних об’єктів з великими труднощами піддаються аналітичному дослідженню. У тих випадках, коли аналітичними методами не вдається з’ясувати загальні властивості моделі, а спрощення моделі спричиняється до недопустимих (неадекватних) результатів, переходять до числових методів дослідження.

4. Підготовка вихідної інформації. Моделювання висуває жорсткі вимоги до системи інформації. Водночас реальні можливості одержання інформації обмежують вибір моделей, які пропонуються до практичного використання. Разом з тим береться до уваги не лише принципова можливість підготовки інформації (за певний період), але й витрати на підготовку відповідних інформаційних масивів. Ці витрати не повинні перевищувати ефект від використання додаткової інформації.

У процесі підготовки інформації широко використовуються методи теорії ймовірностей, теоретичної і математичної статистики. У статистичному економіко-математичному моделюванні результуюча інформація, використовувана в одних моделях, є вихідною для функціонування інших моделей.

5. Числові розв’язки. Цей етап включає розробку алгоритмів для числового розв’язування задачі, складання програм на ЕОМ і безпосереднє проведення розрахунків. Труднощі цього етапу зумовлені передусім великою розмірністю економічних задач, необхідністю опрацювання значних масивів інформації. Звичайно розрахунки на підставі використання економіко-математичної моделі мають багатоваріантний характер. Завдяки високій швидкодії сучасних ЕОМ вдається проводити числові «модельні» експерименти, вивчаючи «поведінку» моделі при різних значеннях деяких умов. Дослідження, які проводяться за допомогою числових методів, можуть стати суттєвим доповненням до результатів аналітичного дослідження. Зазначимо, що клас економічних задач, які можна розв’язувати числовими методами, значно ширший, ніж клас задач, доступних аналітичному дослідженню.

6. Аналіз числових результатів та їх використання. На цьо­му, завершальному, етапі циклу виникає питання про правильність і повноту результатів моделювання, про рівень практичного застосування останніх.

Математичні методи перевірки можуть виявляти некоректність підходу до побудови моделі і тим самим звужувати клас потенційно правильних моделей. Неформальний аналіз теоретичних висновків і числових результатів, які одержують за допомогою моделі, зіставлення їх із знаннями, якими володіємо, і фактами дійсності також дозволять знаходити недоліки постановки економічної задачі, сконструйованої математичної моделі, її інформаційного і математичного забезпечення.

Звернімо увагу на зворотні зв’язки етапів, які виникають унаслідок того, що в процесі дослідження виявляються недоліки попередніх етапів моделювання.

Уже на етапі побудови моделі може з’ясуватися, що постановка задачі суперечлива і призводить до надто складної математичної моделі. Відповідно до цього постановка економіко-математичної задачі коригується. Подальший математичний аналіз моделі (етап 3) може показати, що невелика модифікація постановки задачі чи її формалізації дає корисний аналітичний результат.

Найчастіше необхідність повернення до попередніх етапів моделювання виникає під час підготовки вихідної інформації (етап 4). Може виявитися, що необхідна інформація відсутня чи затрати на її підготовку занадто великі. Тоді доводиться повертатися до постановки задачі та її формалізації, змінюючи їх так, щоб пристосуватися до наявної інформації.

Тема 3 дослідження економічних функцій

План

3.1 Функція витрат

3.2 Функції попиту

3.3 Функції пропозиції

3.4 Функція корисності споживача

3.1 Аналіз витрат містить вивчення впливу витрат виробництва на обсяг виробництва й інші техніко-економічні показники. Найчастіше розглядається функція вигляду:

,

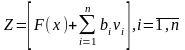де Z - сумарні витрати;

x - кількість продукції;

- параметри моделі;

vi - інші змінні, що характеризують різну структуру ОВФ, різні умови виробництва, різну організацію праці в різних галузях.

Поділимо обидві частини виразу на х

,

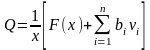де питомі витрати.

Графік питомих витрат показано на рис. 3.1.

Відвернемося від впливу факторів, що, можливо при вивченні витрат у загальнодержавних масштабах. Тоді

Z=f(x),

,

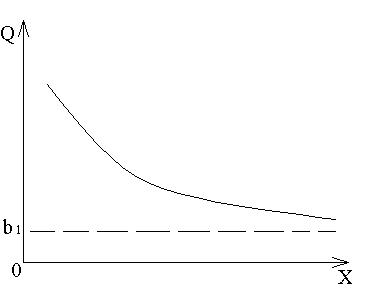
Рис. 3.1

Лінійна функція витрат має вигляд:

Z=f(x)=b0+bix.

Функція питомих витрат буде спадаючою. Параметри можна інтерпретувати за допомогою граничних величин

,

тепер перейдемо від неперервної форми до дискретної

,

тобто фактор ∆Vi при незмінному рівні випуску продукції збільшує витрати на ∆Z ,

∆Z=b i ∆Vi.,

Якщо ∆Vi=1, то ∆Z=bi..

3.2 Функція попиту виражає залежність попиту від економічних (доходи, ціни) і зовнішньоекономічних (споживчі звички) факторів. Функції попиту можуть бути як макроекономічними, якщо охоплюють усю сферу споживання і мікроекономічними, що описують попит індивідуальних споживачів.

D(p) - функція попиту або просто попит (від англ. “demand” - попит) – це кількість товару, що купується на даному ринку за одиницю часу за ціною p за одиницютовару. Фундаментальну властивість функції попиту виражає наступна аксіома: функція попиту є спадаючою, при збільшенні ціни величина попиту на товар зменшується до 0, при зменшенні ціни товару величина попиту збільшується.

Розглянемо наступні функції попиту (рис 3.2):

а) лінійно-спадаюча

D (p) =а-bp, 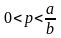, (a,b)>0,

б) обернена

D (p)=1/p, р>0,

в) логарифмічна

D (p)=ln (1+p)/p , p>0.

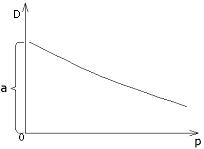
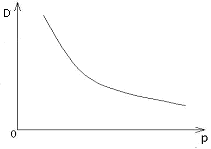
a) б) в)

Рис.3.2

Розглянемо математичні характеристики функції попиту та їхні економічні ілюстрації. Похідна функції попиту за ціною

,

показує наскільки одиниць зміниться величина попиту при зміні ціни товару на одну одиницю.

Еластичність попиту за ціною показує на скільки відсотків зміниться величина попиту при зміні ціни товару на один відсоток. Позначається еластичність

.

3.3 S(p) - функція пропозиції або пропозиція (від англ.“supply” - пропозиція) – це кількість товару, що поставляється на даний ринок за одиницю часу при ціні р за одиницю товару). Функція пропозиції є зростаючою. Аксіома пропозиції: при збільшенні ціни величина пропозиції товару необмежено збільшується, при зменшенні ціни величина пропозиції зменшується, наближаючись до 0.

Розрізняють функції пропозиції (рис. 3.3):

а) лінійно-зростаюча

S (p) = -c + dp, ,

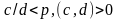б) степенева

,

в) логарифмічна

.

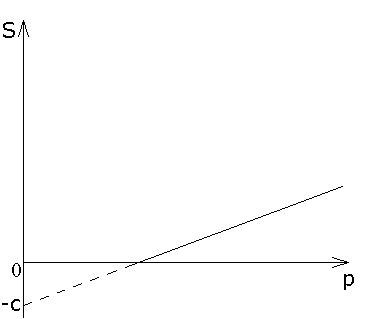
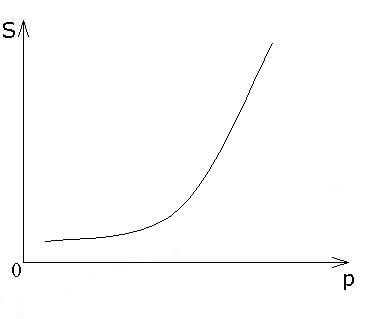
а) б) в)

Рис. 3.3

Розглянемо математичні характеристики функції пропозиції та їхні економічні ілюстрації.

Похідна функції за ціною

,

показує на скільки відсотків зміниться величина пропозиції при зміні ціни товару на одну одиницю.

Еластичність пропозиції за ціною показує на скільки відсотків зміниться пропозиція при зміні ціни товару на один відсоток. Позначається еластичність

.

Знайдемо еластичність пропозиції за ціною для кожної функції, що розглянута вище:

a) ,

;

б) ,

;

в) ,

.

3.4 Рішення споживача щодо купівлі певного набору товарів математично можна подати як вибір точки у просторі товарів. Нехай n — скінченне число видів різноманітних товарів,

де D_i – обсяг товару i-го виду,

- вектор-стовпець споживчих товарів (обсяги), що їх придбав споживач за певний термін (наприклад протягом року) за заданих цін, маючи певний обсяг доходу за цей самий період.

Це означає, що для кожної пари товарів має місце одне з трьох відношень, :

— набір є привабливішим, ніж ;

— набір є менш привабливим, ніж ;

~ — для споживача обидва набори еквівалентні.

Переваги споживача можна подати у фор­мі індикатора переваг, тобто такої функції корисності

, ,

що з випливає ,

з випливає ,

з ~ випливає .

Уведення функції корисності дозволяє замінити відношення переваги звичними відношеннями між числами: більше, менше, дорівнює.

У теорії споживання припускаються гіпотези і вважається, що функція корисності неперерва та диференційована. Вона має такі властивості:

1)  — зі зростанням споживання товару корисність зростає;

2)  - зі зростанням споживання товару швидкість зростання корисності зменшується (спадає);

Розглянемо види функції корисності для товарів двох видів:

1) неокласична

,

2) із взаємозаміщенням

,

3) із взаємодоповненям

,

4) логарифмічна

.

Розглянемо функцію корисності для товарів n видів

.

Гранична корисність товару

,

показує, на скільки зростає корисність, якщо кількість товару зростає в малому обсязі.

Гранична норма заміщення товарів показує, скільки необхідно одиниць j-го товару, щоб замінити малий обсяг і-го товару, який вибув.

.

Припустимо, що функція корисності маї вигляд

,

де р_i – ціна одиниці товару і-го виду,

.

Знайдемо граничні корисності

, .

Розглянемо відношення граничних корисностей

.

Це відношення має назву 2-го закону Госсена.

Тема 4

Моделювання поведінки споживачів

План