
- •Затверджено на засіданні
- •Редактор л.М. Тонкошкур
- •1. Введення в теорію алгоритмів.
- •2. Складність алгоритмів.
- •3. Структури даних.
- •3.1 Статичні та динамічні структури даних.
- •3.2. Стеки
- •3.3. Списки.
- •Блок-схема програми
- •3.4. Черги.
- •Блок-схема програми
- •3.5 Графи.
- •3.6. Дерева.
- •4. Методи побудови ефективних алгоритмів
- •4.1 Метод «розподіляй та володій».
- •Способ 1. Алгоритм пошуку мінімального та максимального значень елементів масиву.
- •Функція MinMax
- •Блок-схема
- •4.4. Жадібні алгоритми
- •5. Алгоритми сортування
- •5.1. Задача сортування та класифікація методів сортування.
- •5.2. Складність алгоритмів сортування.
- •5.3. Швидке сортування (OuickSort).
- •5.4. Сортування деревом (HeapSort) Алгоритм.
- •5.5. Cортування Шелла (ShellSort)
- •5.6. Сортування злиттям (MergeSort)
- •Лінійний пошук - це пошук підряд в неупорядкованій послідовності.
- •7. Алгоритми на графах.
- •Список літератури
Лінійний пошук - це пошук підряд в неупорядкованій послідовності.
Двійковий пошук - це пошук в упорядкованій послідовності. Структурой даних, яка дозволяє виконати двійковий пошук є дерево двійкового пошуку (тема «Структури даних»).
Метод розміщення (хеширування):
Функція розміщення h (хеш-функція) відображає елементи універсальної множини S в множину A цілих чисел від 0 до m-1. Компонентами масива А (таблиця розміщення або хеш-таблиця), розміром m служать покажчики на списки елементів множини S. Список, на який указує А[i] складається з усіх тих елементів а з множини S, для яких h(a)=i.
Таблиця розміщення (хеш-таблиця):
Список
для h(a)=0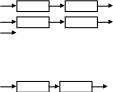
0 |
Список для h(a)=1 |
2 |
. |
. |
. |
Список
для+h(a)=m-1 |
Таким чином масив А – це таблиця розміщення (хеширування)
Приклад.
Нехай елементами являються ланцюжки з букв і використовується наступна функція розміщення (хеш-функція) для таблиці розміру m=5:
скласти «значення» букв, де A має значення 1, B - значение 2 і т.д.;
розділити результат на 5 і узяти залишок.
Вивести уміст таблиці розміщення і списків, при умові, що вставляються ланцюжки:
KEY, STRUCT, RECORD, OBJECT.
Алгоритм:
В якості хеш-функції візьмемо: h(a)=a mod m, де m=5 (залишок від ділення на 5).
ЛАТИНСЬКИЙ АЛФАВІТ:
1 - A, 2 - B, 3 - C, 4 - D, 5 - E, 6 - F, 7 - G, 8 - H, 9 - I, 10 - J, 11 - K, 12 - L, 13 - M, 14 - N, 15 - O, 16 - P, 17 - Q, 18 - R, 19 - S, 20 - T, 21 - U, 22 - V, 23 - W, 24 - X, 25 - Y, 26 - Z.
Тоді:
KEY=11+5+25=41 : h=41 mod 5=1;
STRUCT=19+20+18+21+3+20=83 : h=83 mod 5=3;
RECORD=18+5+3+15+18+4=63: h=63 mod 5=3;
OBJECT=15+2+10+5+3+20=55: h=55 mod 5=0;
Таблиця розміщення (хеширування)
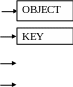 А
А
0
|
1
|
Порожній список
|
STRUCT
RECORD
|
7. Алгоритми на графах.
Задача Прима-Краскала.
Дан граф з n вершинами. Довжини ребер задані матрицей {cij}, де i, j = 1,…,n. Зайти остовне дерево мінімальної ваги.
Остовним деревом для графа називається неорієнтоване дерево, яке містить всі вершини графа. Вартість або вага остовного дерева визначається як сума вартостей його ребер.
Алгоритм Прима-Краскала:
Спочатку покрасимо i-у вершину в відмінний від інших кольор i, тобто всі вершини різнокольорові. Для побудови остовного дерева мінімальної ваги необхідно кожного разу обирати вершини різного кольору, відстань між якими найменша. При виборі такого чергового ребра найменшої довжини (i, j) вершина j та всі вершини її кольору (тобто раніше з нею з’єднані) перекрашуються в кольор i. Таким чином вибір вершин різного кольору забезпечує відсутність циклу. Після вибору (n-1) ребер всі вершини отримують один кольор.
Приклад. Знайти дерево мінімальної ваги для заданого графа:
 20
20


 1
2
1
2

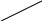
23 1 4 15
36 9
 6 7
3
6 7
3

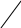


25 16
28 3
5 4
17
1 7 - кольор вершин 1, відстань 1;
3 4 - кольор вершин 3, відстань 3;
7 2 - кольор вершин 1, відстань 4;
7 3 - кольор вершин 1, відстань 9;
4 5 - кольор вершин 1, відстань 17;
1 6 - кольор вершин 1, відстань 23.







Вага остовного дерева: 1+3+4+9+17+23 = 57.

 3
3