5.2. Складність алгоритмів сортування.

Теорема. У кожному алгоритмі, який упорядковує за допомогою порівнянь, на упорядкування послідовності з n елементів втрачається О(nlog₂ n) (не менше) порівнянь при достатньо великому n.

Доказ:

Результатом порівнянь n елементів може бути n! перестановок. Згідно за формулою Стірлінга n! точніше наближує функція (n/e)ⁿ. Тому, при логарифмуванні маємо:

log₂(n!)  log₂(n/e)ⁿ = n(log₂n – log₂e) = nlog₂n – 1.44n = O(nlog₂n) – нижня границя алгоритмів сортування (не менш за nlog₂n).

Розглянемо деякі методи сортування: чотири поліпшених методи (швидкого сортування, деревом, Шелла, злиттям) зі складністю О(nlog₂n) та три методи зі складністю О(n²).

Задача.

Відсортувати в порядку неубування елементи цілочисельного масиву А з n елементів.

5.3. Швидке сортування (OuickSort).

Алгоритм.

Вхід: масив сортуємих елементів А.

Вихід: відсортований масив А.

Крок 1. 1.) Вибрати навмання елемент х одним з способів:

за допомогою генератора випадкових чисел;

2.) х = А[i] = А[ (1+n)/2 ] (медіана).

Крок 2. Переглядати масив ліворуч, доки не знайдеться елемент А[і] > х.

Крок 3. Переглядати масив праворуч, доки не знайдеться елемент А[і] < х.

Крок 4. Поміняти місцями А[i] та А[j].

Крок 5. Продовжити процес перегляду та обміну (кроки 1-4), доки вони не зустрінуться

(i = j). Результат: масив поділено на ліву частину, де всі елементи менші за х та праву, де всі елементи не менші за х .

Крок 6. Застосувати кроки 1-5 до кожної з одержаних частин, доки в кожній з частин не залишеться по одному елементу.

5.4. Сортування деревом (HeapSort) Алгоритм.

Вхід: масив елементів (вузлів) сортування А, де А [1]- елемент в корені.

Вихід: елементи масива А, організовані у вигляді сортуючого дерева, тобто:

A[i]<=A[n/2] , 1< i <n

Крок 1. Вузли дерева помітити елементами масиву, який треба відсортувати.

Крок 2. Міняти розміщення елементів (вузлів), доки кожен вузел стане не меншим за його -нащадків. Таке дерево називають сортуючим.

Крок 3. Найбільший елемент, який відповідає кореню дерева, видаляється, а в корень переноситься елемент самого останнього листа. Перехід до кроку 2. Якщо на дереві залишився тільки один елемент, то перехід до кроку 4.

Крок 4. Результатом є послідовність елементів, видалених з сортуючого дерева, впорядкована по убуванню.

5.5. Cортування Шелла (ShellSort)

Алгоритм.

Крок 1. Масив з n елементів А розбити на k груп по 2 елементи в кожній таким чином, щоб елементи кожної групи розташувались на відстані d один від одного. d-крок групи, повинен бути ступенем двох (або d n/2).

Крок 2. Відсортувати елементи в кожній з груп, наприклад методом пузирькового включення.

Крок 3. k і d зменшують удвічі. Перейти до кроку 2. Якщо d дорівнює 1, перейти до кроку 2 і потім завершити сортування.

5.6. Сортування злиттям (MergeSort)

Алгоритм. (сортування методом «розподіляй і володуй»)

Крок 1. Масив елементів А розбити на 2 частини В і С.

Крок 2. Частини В і С зливаються, при цьому одиночні елементи утворюють упорядковані пари.

Крок 3. Перейти до кроку 1, при цьому упорядковані пари переходять в такі ж четвірки.

Крок 4. Повторюючи кроки 1-2, зливаємо четвірки в вісімки і так далі, доки не буде упорядковано весь масив А.

5.7. Пухирцеве включення (BubbleInsertion)

Складність методів, наведених нижче, має порядок О(n²) (максимальна кількість порівнянь).

В сортуванні включенням кожен елемент почергово порівнюється з попередніми і шукається місце включення цього елементу.

Алгоритм.

5.8. Пухирцеве всплиття (BubbleSort)

В сортуванні «пухирцем» послідовно порівнюються елементи, що стоять поруч, і в разі необхідності обмінюються місцями. Таким чином, поступово найбільші по значенню елементи «вспливають» в кінці масиву.

Алгоритм.

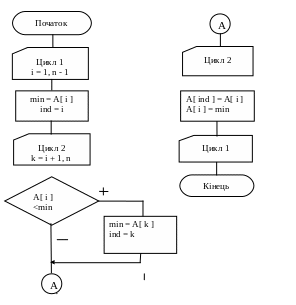
5.9. Простий вибір

Сортування методом простого вибору передбачає пошук мінімального елементу і заміну місцем з першим елементом. При виконанні цієї процедури (n – 1) разів поступово найменші елементи вишикуються на початку масиву.

Алгоритм.

6. Алгоритми пошуку.

Однією з основних задач нечисловоЇ обробки даних є задача пошуку. Так як звичайно об'єкт (елемент) має декілька властивостей, то пошук здійснюється по ключу, наприклад:

Type item=record

key: integer;

{информаційне поле}

end;