4. Методи побудови ефективних алгоритмів

4.1 Метод «розподіляй та володій».

Для рішення задачі її часто розбивають на частини, знаходять їх рішення, потім з них отримують рішення всієї задачі. Цей метод, особливо якщо його застосовувати рекурсивно, часто приводить до ефективного рішення задачі, підзадачі якої представляють її менші версії.

Розглянемо задачу пошуку мінімального та максимального значень елементів множини двома способами – звичайним алгоритмом пошуку мінімального та максимального значень елементів масиву та з застосуванням методу «розподіляй та володій».

Способ 1. Алгоритм пошуку мінімального та максимального значень елементів масиву.

+

-

-

+

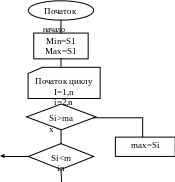
Min=Si

Кількість порівнянь:

(n-1) – пошук максимального значення;

(n-2) – пошук мінімального значення;

(2n-3) – всього порівнянь.

Способ 2. Алгоритм з застосуванням методу «розподіляй та володій».

Множина S разбивається на дві однакових підмножини S1 и S2, кожна з яких також розбивається на підмножини, доки в кожній з них не залишеться по два елементи, один з яких- мінімальний, інший - максимальний. Знайдені рішення об’єднуються, серед них знову обчислюються мінімум та максимум, і так далі. Потім з них отримують рішення всієї задачі (рекурсивна функція MinMax).

Функція MinMax

+ -

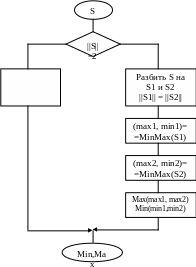
Обчислимо кількість порівнянь.

Нехай Т(n) - число порівнянь у функції MinMax.

Відомо, що Т(2)=1, тоді Т(n) можна представити наступним чином:

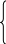1 , при n =2

T(n) =

, при n>2

Рішенням цих рекурсивних рівнянь є функція

Докажемо це методом математичної індукції.

Відомо, що при n = 2 Т(2) =1.

Припустимо, що при n =m це рішення вірно, тобто

Докажемо, що при n=2*m функція T(n) задовільняє рекурентному рівнянню:

.

Що і потрібно було доказати.

Звідси кількість порівнянь алгоритму з застосуванням методу «розподіляй та володій» дорівнює

Порівняємо алгоритм 1 і алгоритм 2. Алгоритм 1 має (2n-3) порівнянь, а алгоритм 2 має порівнянь. Таким чином, алгоритм з застосуванням методу «розподіляй та володій» ефективніший.

4.2. Рекурсія.

Рекурсія - це можливість ввести в визначення об’екту посилання на сам об’єкт. Рекурсія є одним з фундаментальних концептуальних інструментів, наявних в розпорядженні програміста.

Приклад.

Визначити рекурсивну функцію обчислення xⁿ для x>0 і n>0.

Блок-схема програми

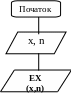
Блок-схема функції EX

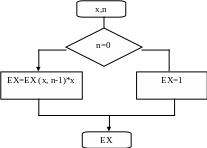
так

ні

Текст програми:

#include <iostream.h>

int EX(int, int);

void main()

{

int x,n;

cout<<”input x,n”<<endl;

cin>>x>>n;

cout<<”Result:”<<endl;

cout<<EX(x, n)<<endl;

}

int EX(int x, int n)

{

if (n==0)

return 1;

else

return EX(x, n-1);

}

4.3. Метод динамічного програмування

Динамічне програмування - це табличний метод, при якому використовується одна й та же схема для обчислення всіх підзадач даної задачі. В цьому методі одного разу знайдений результат записується в таблицу и далі повторно не обчислюється.

Динамічне програмування застосовується до задач оптимізації.

Приклад. Знайти добуток чотирьох матриць з мінімальною складністю, тобто необхідно вибрати оптимальний порядок множення матриць.

Припустимо, що множення матриці розміром p*q на матрицю розміром q*r потребує p*q*r операцій.

Знайдемо добуток чотирьох матриць М = М1*М2*М3*М4 розміром

М1 = [10*20] , М2 =[20*50] , М3 = [50*1] , М4 = [1*100].

Позначимо r₀ =10, r₁ =20 , r₂ =50 , r₃ =1 , r₄ =100.

Обчислення матриць в порядку М1*(M2*(M3*M4)) потребує таку кількість операцій:

50*1*100+20*50*100+10*20*100 =125000

Обчислення в порядку (М1*(M2*M3))*M4 потребує таку кількість операцій:

20*50*1+10*20*1+10*1*100 = 2200.

Ці результати отримані шляхом перебору варіантів порядку множення матриць.

Розглянемо алгоритм, що дозволить відразу обрати оптимальний порядок множення матриць.

Алгоритм динамічного програмування для обчислення порядку, що мінімізує складність множення ланцюжку з n матриць:М1*М2*М3*…*Мn.

Позначимо:

r₀, r₁ , … , r_n , де r_i-1 и r_i - кількість рядків і стовпців матриці М_і, i=1,n;

m_ij -мінімальна складність обчислення добутку матриць М_і * Мі₊₁ * …* М_j;

m_ik - мінімальна складність обчислення добутку матриць М_і * Мі₊₁ * …* М_k=M';

m_k+1,j - мінімальна складність обчислення добутку матриць М_k+1 * М_k+2 * …* *М_j = M".

r_i-1 * r_{k *} r_{j -} - складність множення M' * M".

Тоді:

m_ij = 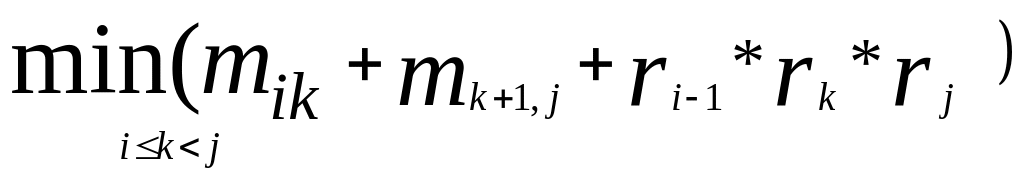, якщо j>i,

m_ij = 0, якщо i = j.

Алгоритм динамічного програмування для обчислення порядку, що мінімізує складність множення ланцюжку з n матриць:М1*М2*М3*…*Мn, наведений на блок-схемі.

Результат обчислення значень m_ij заносимо в таблицю:

m11 = 0	m22 = 0	m33 = 0	m44 = 0
m12 = 10000	m23 = 1000	m34 = 5000
m13 = 1200	m24 = 3000
m14 = 2200

Порядок, в якому можна виконати множення матриць, визначається таким чином: ожній клітині таблиці приписується те значення k, при якому досягається мінімум. Таким чином, мінімальна кількість операцій дорівнює 2200.