Блок-схема програми

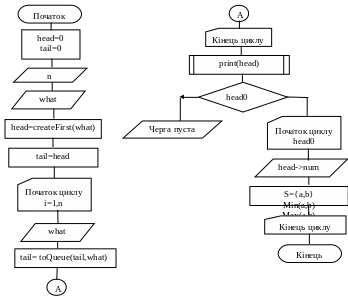
Текст програми:

#include <iostream.h>

struct node

{

int num;

node *next;

};

node* createFirst(int);

node* toQueue(node* ,int);

node* fromQueue(node* );

void print(node*);

void main()

{

int what,i,n;

node *head=0, *tail=0;

cout<<"input n=";

cin>>n;

cout<<endl;

cout<<"input first what"<<endl;

cin>>what;

cout<<endl;

head=createFirst(what);

tail=head;

cout<<"input all what"<<endl;

for (i=1;i<n;i++)

{

cin>>what;

tail= toQueue(tail ,what);

}

print(head);

if (!head)

cout<<"Queue is nil\n";

else

{

cout<<"fromQueue:"<<endl;

while(head)

{

cout<<head->num<<" ";

head=fromQueue(head);

}

cout<<endl;

}

}

node* createFirst(int num)

{

node* pv=new node;

pv->num=num;

pv->next=0;

return pv;

}

node* toQueue(node* tail ,int num)

{

node* pv=new node;

pv->num=num;

pv->next=0;

tail->next=pv;

tail=pv;

return tail;

}

node* fromQueue(node* head)

{ int num;

node* old=head;

head=head->next;

delete old;

return head;

}

void print(node* pv)

{

if (!pv)

cout<<"Queue is nil\n";

else

while(pv)

{

cout<<"="<<pv->num<<endl;

pv=pv->next;

};

}

3.5 Графи.

Граф G =(V,E) складається з кінцевої непустої множини вузлів V и множини ребер E. Якщо ребра представлені в вигляді впорядкованих пар вузлів (v,w) (кожному ребру приписується напрям), то граф називається орієнтованим.

Якщо кожному ребру приписується довжина (вага), то граф називається мережею та позначають N (V,E,W).

Структури даних для представлення графів.

Граф G=(V,E) можно представити в вигляді:

1. матриці суміжностей:

Наприклад, для графа, представленого на рисунку матриця має вигляд:

2. списка суміжностей:

в

2

4 0

узел 1

в

3 0

узел 2

вузел 3 пустой список

в

2

3 0

узел 4

Представлення графа в вигляді матриці суміжностей зручно для тих алгоритмів, яким необхідно знати, чи є в графі дане ребро, тому що час для визначення наявності ребра – фіксований і не залежить від кількості вузлів і кількості ребер. Недолік – матриця займає пам’ять об’ємом ||V|| , навіть коли граф має тільки O(||V||) ребра і потребує на заповнення часу O(||V|| ).

Представлення графу в вигляді списків суміжностей вимагає пам’яті порядка ||V||+||E||. Цим представленням користуються, коли ||E||< =||V|| .

3.6. Дерева.

Дерева – це вид орієнтованого графа.

ВИЗНАЧЕННЯ:

1. Орієнтований граф без циклів називається орієнтованим ацикличним графом.

2. Орієнтоване (кореневе) дерево - це орієнтований ацикличний граф, що задовольняє наступним умовам:

а) мається в точності один вузол, називаний коренем, у який не входить жодне ребро;

б) в кожен вузол, крім кореня, входить рівно одне ребро;

в) з кореня до кожного вузла йде єдиний шлях.

3. Якщо (v,w) належить множині ребер Е и v<>w, то v називається справжнім предком (батьком) вузла w, а w - справжнім нащадком (сином) вузла v.

4. Вузол без справжніх нащадків називається листом.

5. Упорядкованим деревом називається дерево, у якому безліч синів кожного вузла упорядковане (приймається, що упорядковано зліва направо).

6. Двійковим (бінарним) деревом називається таке упорядковане дерево, що:

а) кожен син довільного вузла ідентифікується або як лівий син, або як правий син;

б) кожен вузол має не більш одного лівого і не більш одного правого сина.

Двійкові (бінарні) дерева використовують для сортування і пошуку даних.

Кожен елемент (вузол) дерева являє собою запис виду:

struct node

{ float num //ключове поле

//інформаційні поля

node *left; // покажчик на лівий елемент

node *right; // покажчик на правий елемент

};

ПРИКЛАД.

Організувати дані в вигляді черги. Вивести на екран елементи черги з одночасним видаленням із пам’яті.

Текст програми::

#include <iostream.h>

struct node

{

int d;

node *left;

node *right;

};

node * first(int d);

node * search_insert(node *root, int d);

void print_tree(node *root, int l);

void main()

{

int n, i, what;

cout<<"input n \n";

cin>>n;

cout<<"input first what \n";

cin>>what;

node *root = first(what);

for (i = 1; i<n; i++)

{

cout<<"input what \n";

cin>>what;

search_insert(root, what);

}

print_tree(root, 0);

}

node * first(int d)

{

node *pv = new node;

pv->d = d;

pv->left = 0;

pv->right = 0;

return pv;

}

node * search_insert(node *root, int d)

{

node *pv = root, *prev;

int found = 0;

while (pv && !found){

prev = pv;

if (d == pv->d) found = 1;

else if (d < pv->d)pv = pv->left;

else pv = pv->right;

}

if (found) return pv;

node *pnew = new node;

pnew->d = d;

pnew->left = 0;

pnew->right = 0;

if (d < prev->d)

prev->left = pnew;

else

prev->right = pnew;

return pnew;

}

void print_tree(node *p, int level)

{

if (p)

{

print_tree(p->left, level+1);

for (int i = 0; i<level; i++)

cout << " ";

cout << p->d << endl;

print_tree(p->right, level + 1);

}

}