1. Введення в теорію алгоритмів.

Предметом навчальної дисципліни «Теорія алгоритмiв» є вивчення методів та засобів побудування ефективних алгоритмів.

У процесі вивчання дисципліни студенти мають засвоїти методи побудови ефективних алгоритмів, програмну реалізацію цих алгоритмiв з використанням ефективних структур даних, вміти виконати оцінку складності алгоритму.

Зміст дисципліни розкривають такі теми:

Складність алгоритмiв. Структури даних. Методи побудови ефективних алгоритмів. Алгоритми сортування. Алгоритми пошуку. Алгоритми на графах.

АЛГОРИТМ - це строга система правил, яка визначає послідовність дій над об’єктами.

АЛГОРИТМ - це точний і строгий опис послідовності операцій, який дозволяє за кінцеву кількість кроків отримати рішення задачі.

ВИМОГИ ДО АЛГОРИТМІВ:

Опис даних (вхідних, вихідних, внутрішніх) і вимог до них.

Алгоритм повинен складатися з окремих елементарних кроків.

Детермінованість алгоритма, тобто. після кожного кроку вказується, який крок виконати дальше, або дається команда закінчення алгоритма.

Результативність алгоритма, тобто закінчання роботи алгоритма після кінцевої кількості кроків з вказанням результата.

Масовість, тобто алгоритм призначений для рішення цілого класу задач.

2. Складність алгоритмів.

Складність алгоритма характеризує час виконання алгоритма та кількість необхідної пам’яті (часова та ємнісна складність).

Практична складність є точною мірою часу обчислювань і об’єма пам’яті для конкретної моделі обчислювальної машини.

Теоретична складність більш незалежна від практичних умов виконання алгоритма та дає порядок величини часу обчислювань і об’єма пам’яті.

ПРИКЛАД.

Для любого цілого n>1 знайти його найбільший ділитель (НД), відмінний від n. Якщо n – просте число, то результатом є число1.

Алгоритм А.

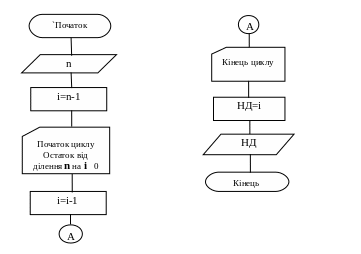
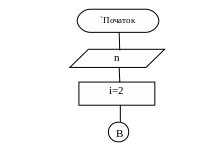
Алгоритм В.

Алгоритм В оснований на тому, що результатом є n/i, де i - найменший ділитель цілого числа n, більший за 1. Якщо n – просте число, то найменший ділитель дорівнює 1, інакше найменший ділитель знаходиться проміж числами 2 і .

Схематично обидва алгоритми мають вигляд:

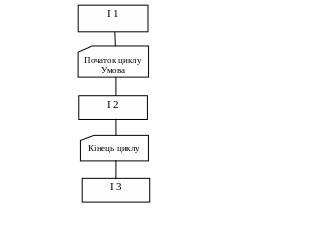Позначемо:

t1 – час виконання операторів I 1.

t2 - час виконання операторів I 2.

t3 - час виконання операторів I 3.

Цикл з передумовою складається з одного умовного та одного безумовного переходів, які потребують часу відповідно tу і tб. Тоді час виконання кожного з алгоритмів А и В визначається так:

t = t1+ t3+m ( tу +t2+tб) + tу

де m - число повторень циклу (у кожного алгоритму своє).

Або:

t = P + Qm

де P = t1+ t3+ tу; Q = tу +t2+tб.

Тоді для алгоритма А максимальне число виконання циклу m дорівнює:

m = n-2.

Для алгоритму В максимальне число виконання циклу m дорівнює:

m = - 2, д е - округлення числа х до найближчого більшого цілого.

Таким чином максимальний час виконання, тобто часова складність визначається в вигляді:

a+b*n - для алгоритма А ;

a’+b’* - для алгоритма В.

Для обчисления практичної складності алгоритму необхідно обчислити константи a, b, a’, b’, які визначаються конкретною моделлю ЕОМ і залежать від часу виконання її команд.

Теоретичена складність: алгоритм А має складність порядка n, тобто O(n), а алгоритм В відповідно O( ), де О означає “величина порядка”.

Якщо n = 10 , то алгоритм В має складність порядку 10 , а алгоритм А – порядку 10 , звідки видно перевагу алгоритма В.

Таким чином критерієм оцінки алгоритма є порядок росту необхідних для рішення задачі часу та ємності пам’яті при збільшенні вхідних даних.

Розмір задачі - це міра кількості вхідних даних.

Час, який витрачається алгоритмом як функція розміру задачі, називається часовою складністю алгоритма(t=f(n)).