22. Теодолитный ход. Виды теодолитных ходов. Прямая геодезическая задача. Формулы для вычисления координат точек.

Теодолитным ходом называют построенную на местности разомкнутую или замкнутую ломаную линию, в которой измерены все стороны и горизонтальные углы между ними, т. е. в основу теодолитного хода положен метод полигонометрии.

Теодолитные ходы (рис. 22.1) с допустимыми относительными невязками l/T-ƒ_s/[s], где ƒ_s — абсолютная невязка в теодолитном ходе; [s] — длина хода между исходными пунктами, прокладывают с соблюдением требований, приведенных в таблице

Масштаб	ms = 0,2 мм			ms = 0,3 мм
	1/T = 1/3000	1/N = 1/2000	1/T = 1/1000	1/T = 1/2000	1/T = 1/1000
	Допустимые длины ходов между исходными пунктами, км
1:5000	6,0	4,0	2,0	6,0	3,0
1:2000	3,0	2,0	1,0	3,6	1,5
1:1000	1,8	1,2	0,6	1,5	1,5
1:500	0,9	0,6	0,3	-	-

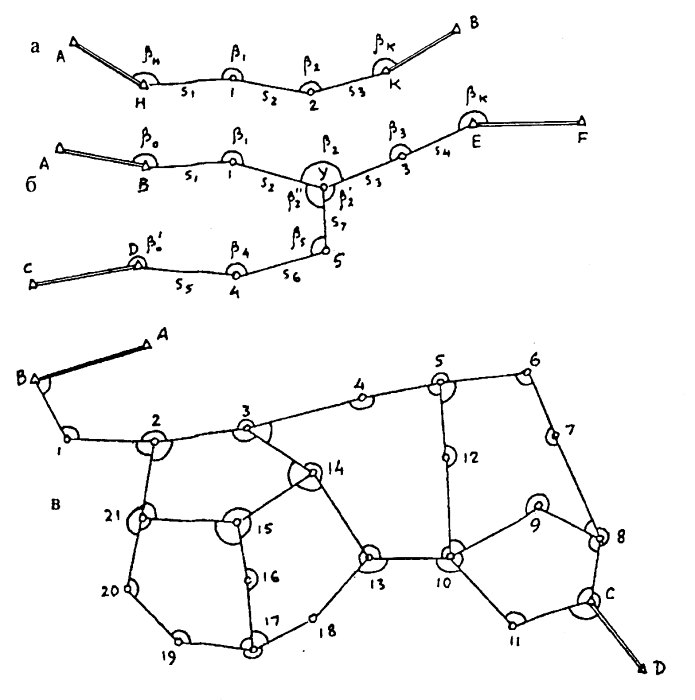
Рис. 22.1. Схемы теодолитных ходов: а) — одиночного; б) — с одной узловой точкой; в) — с несколькими узловыми точками

Замкнутый вид хода реализуют положением теодолитного хода по контуру снимаемого объекта с привязкой этого хода к съемочному обоснованию. Данный метод используют, как правило, в закрытой местности для обозначения недоступных объектов значительной площади: болота, запретные зоны, территории хозяйственных объектов и т.д.

Суть разомкнутого вида состоит в том, что на прямой между двумя известными точками, размещенными на сторонах съемочного обоснования с помощью одного из мерных приборов определяют положение характерных ситуационных точек местности. Данный метод находит применение, главным образом, при изысканиях аэродромов, для установления ситуационных особенностей местности в ходе топографических съемок методом геометрического нивелирования по квадратам.

По измеренным сторонам и углам определяют прямоугольные координаты вершин теодолитного или тахеометрического хода, а по измеренным вертикальным углам и длинам сторон — превышения между точками тахеометрического хода, т. е. теодолитным ходом определяют плановое положение вершин хода, а тахеометрическим ходом — плановое и высотное их положение. На рисунке 22.2 изображена часть теодолитного хода. Для точки 1 координаты

   ( 22.3)

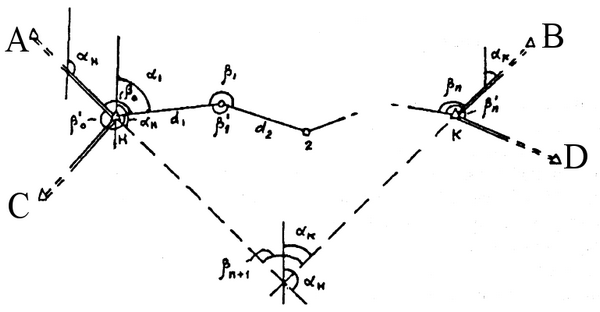
Рис. 22.2. Схема разомкнутого теодолитного хода

Формулы (22.3) решают прямую геодезическую задачу на плоскости, в которой при известных прямоугольных координатах х_H,у_H, горизонтальном проложении d и дирекционном угле а требуется определить координаты х₁, у₁, точки 1.

В обратной задаче по известным координатам х₁,у₁; х₂,у₂, точек 1 и 2 (рис. 22.4) требуется определить дирекционный угол α и горизонтальное проложение d.

Рис.22.4 Решение обратной задачи на плоскости

На рисунке 22.4 из прямоугольного треугольника 122'

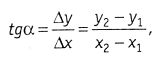        (22.5)

откуда находят дирекционный угол  α. Горизонтальное проложение

      (22.6)

Измерив горизонтальный угол β₀ между исходной и определяемой сторонами, на pисунке 22.3 имеем

      (22.7)

если измерены левые по направлению теодолитного хода углы.

Если измерены правые углы β'_0' β'₁  и т.д., то, учитывая β₀ = 360° - β'₀, вместо формулы (22.7) находим

       (22.8)

Следовательно, для определения координат точек теодолитного хода необходимо начинать ход с опорной точки, имеющей координаты х_H,у_H, и в этой начальной опорной точке измерить примычный угол β₀ и β'₀ между линией с известным дирекционным углом и линией d1 хода.

Определение координат точек хода вычисляется формулам:

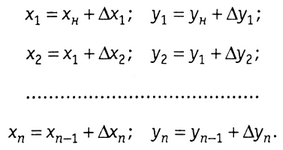
В результате х_n, у_n в разомкнутом и х_n = x, y_n = y_н  в замкнутом  и ходах должны совпадать с их известными для опорных точек значениями.