5. Активные и индуктивные сопротивления обмоток

5.1 Сопротивление обмотки статора

111. Активное сопротивление обмотки фазы r₁ при 20С найдём по формуле (9–178).

r₁ = ₁l_СР1/(_М20а₁сS 10³);

r₁ = 360  423,99/(57  1 10,503  10³) = 5,32 Ом.

112. Активное сопротивление обмотки фазы r_1 при 20С в относительных единицах найдём по формуле (9–179).

r_1 = r₁I₁U₁;

r_1 = 5,32 3/220 = 0,073.

113. Проверка правильности определения r_1 по формуле (9–180).

;

114. Размеры паза статора определим из рисунка 9–7, §9–4, таблицы 9–21:

b₂=5,18мм; b_ш1=2,7мм; h_ш1=2,7мм; h_k1=0,7мм; h₂=0,6; h_п1=16мм.

h₁=12 мм.

115. Т.к. двигатель является двигателем малой мощности (до 10кВт), то он имеет однослойную обмотку, а следовательно =1, k_1=1.

116. Коэффициент проводимости рассеяния для трапецеидального полуоткрытого паза _П1 найдём по (9–185).

.

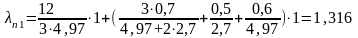117. Коэффициент k_д1 берем из таблицы (9–23), при q₁ = 2.

k_д1 = 0,0285.

118. Коэффициент, учитывающий влияние открытия пазов статора на проводимость дифференциального рассеяния по формуле (9–188).

.

119. Коэффициент k_р1 берем из таблицы (9–22) при q₁ = 2, Z₂ = 628 и р = 3.

k_р1 = 0,880.

120. Коэффициент проводимости дифференциального рассеяния _Д1 найдём по формуле (9–189).

_Д1 = 0,9(t_1mink_об1)²k_р1k_ш1k_Д1/(k_);

_Д1 = 0,9·8,46·0,97²  0,880  0,888  0,0285/(0,25  1,38) =3,881.

121. Полюсное деление  найдём по формуле (9–190).

₁ = D₁  2р;

₁ = π  97/6 = 51 мм.

122. Коэффициент проводимости рассеяния лобовых частей обмотки _Л1 найдём по формуле (9–191).

_Л1 = 0,34(q₁  l₁)(l_Л1 – 0,64₁);

_Л1 = 0,34  (2/105)(107 – 0,64 · 1 · 51) = 0,48.

123. Коэффициент проводимости рассеяния обмотки статора ₁ найдём по формуле (9–192).

₁ = _П1 + _Д1 + _Л1;

₁ = 1,316 + 3,881 + 0,48 = 5,680.

124. Индуктивное сопротивление обмотки фазы статора x₁ найдём по формуле (9–193).

x₁ = 1,58f₁l₁²₁₁  (pq₁  10⁸);

x₁ = 1,58  50 105 360²  5,680 /(3  2  10⁸) = 10,176 Ом.

125. Индуктивное сопротивление обмотки фазы статора x_1 в относительных единицах найдём по формуле (9–194).

x_1 = x₁I₁  U₁;

x_1 = 10,176  3 / 220 = 0,139.

126. Проверку правильности определения x_1 в относительных единицах произведём по формуле (9 – 195).

x_1 = 0,39(D₁A₁)²l₁₁ 10^-7(m₁U₁I₁z₁);

x_1 = 0,39(97  212,96)² · 105  5,680 10^-7/(3  220  3  36) = 0,139.

5.2 Сопротивление обмотки короткозамкнутого ротора

127. Активное сопротивление стержня клетки r_ст найдём по формуле (9–196).

r_ст = l₂/(_аS_СТа₂  10³)

r_ст = 105/(2737,210³)=10,4510^-5Ом.

128. Коэффициент приведения тока кольца к току стержня найдем по формуле (9–198).

k_ПР2 =2πp/z₂;

k_ПР =23,143/64= 0,3.

129. Сопротивление короткозамыкающих колец, приведенные к току стержня при 20^◦С (Ом) найдём по формуле (9–199).

r_кл =2πD_кл.ср/_а20z₂S_клk²_пр210³, Oм;

r_кл = 23,1477,30/272890,850,673²10³=1,56·10^-5 Ом._.

130. Центральный угол скоса пазов найдём по формуле (9–200).

ά_ск=2pt₁β_ck1/D_1, рад;

ά_ск=238,46/97=0,523 рад.

131. Коэффициент скоса пазов ротора находим по рисунку (9-16). k_ск = 0,4 + 0,6₂; (5.19)

k_ск =0,996;

132.Коэффициент приведения сопротивления обмотки ротора к обмотки статора найдем по формуле (9-201).

K_пр1 =

k_пр1=

133. Активное сопротивление обмотки ротора при 20^◦С приведенное к обмотке статора (Oм) найдем по формуле (9–202).

r^’₂ = k_пр1(r_ст+r_кл)

r^’₂=52291(7,99+1,56) 10^-5 = 4,994 Oм.

134. Активное сопротивление обмотки ротора при 20^◦С приведенное к обмотке статора (о.е.) найдем по формуле (9–203).

r^’_2*=r₂^’I₁/U₁;

r^’_2*=4,9943/220=0,068.

135. Ток стержня ротора для рабочего режима найдем по формуле (9-204).

I₂= , A

I₂= A

136. Коэффициент проводимости рассеяния _п2 найдём по формуле (9–205).

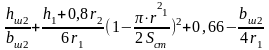_п2 = ;

_п2 =

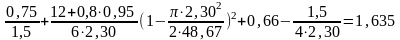
137. Количество пазов ротора на полюс и фазу найдем по формуле (9–8а).

q₂ =z₂/(2pm);

q₂ =28/(63)=1,556.

138. Коэффициент дифференциального рассеяния ротора найдем по рисунку (9-17).

k_д2=0,025;

139. Коэффициент проводимости дифференциального рассеяния по формуле (9-207).

λ_д2=0,9t₂(z₂/6p)²k _д2/(δk_δ);

λ_д2=0,9·10,82·(28/(6·3))²0,025/(0,251,38)=1,707;

140. Коэффициент проводимости рассеяния короткозамыкающих колец литой клетки найдем по формуле (9-208).

λ_кл=

λ_кл=

141. Относительный скос пазов ротора, в долях зубцового деления ротора найдем по формуле (9-209).

Β_ск2= Β_скt₁/t₂;

Β_ск2=18,46/10,82 = 0,782.

142. Коэффициент проводимости рассеяния пазов найдем по формуле (9-210).

λ_cк=t²β²_ск2/(9,5δk_δk_нас);

λ_cк=10,820,782²/(9,50,251,381,935) = 1,043.

143. По формуле (9–211) определим коэффициент проводимости рассеяния обмотки ротора ₂.

₂=_п2+_д2+_кл+_ск

₂=1,635+1,707+0,148+1,043=4,533.

144. Индуктивное сопротивление обмотки ротора x₂ найдём по формуле (9–212).

x₂ = 7,9f₁l₂₂ 10^-9;

x₂ = 7,9  50  105  4,533  10^-9 = 0,2·10^-3 Ом.

145. Индуктивное приведённое сопротивление обмотки ротора x₂ найдём по формуле (9–213).

x₂ = k_пр1 x₂;

x₂ = 52291  0,2  10^-3 = 9,830 Ом.

146. Индуктивное приведённое сопротивление обмотки ротора x_2 в относительных единицах найдём по формуле (9–214).

x_2 = x₂I₁  U₁;

x_2 = 9,830  3/220 = 0,134.

147. Проверка правильности определения x₂ производим по формуле (9–215).

x₁/ x₂  0,7 1,0;

10,176/9,830 = 1,03.