Метод переміщень. Розгорнута форма методу переміщень. Основні невідомі. Рівняння рівноваги та їх зміст. Наведіть приклад.

7.4 Алгоритм расчета систем методом перемещений

Расчет статически неопределимых систем методом перемещений выполняется в следующей последовательности:

1. Находим степень кинематической неопределимости заданной системы.

2. Выбираем основную систему.

3. Записываем канонические уравнения метода перемещений.

4. Строим единичные и грузовые эпюры изгибающих моментов для основной системы.

5. Определяем коэффициенты и свободные члены системы канонических уравнений.

6. Проверяем правильность вычисления коэффициентов и свободных членов системы канонических уравнений.

7. Вычисляем значения неизвестных метода перемещений.

8. Строим эпюры N, Q, M для заданной системы.

9. Проверяем правильность построения окончательных эпюр.

3.  Система  канонічних  рівнянь методу переміщень, яка виражає  умову рівності нулю реакцій в додаткових зв'язках, має такий вигляд:

(2.3.2)

де   – реактивне зусилля в i–му додатковому зв'язку, викликане одиничним вимушеним  переміщенням  j–го зв'язку;        i=1, 2, 3…n;     j=1, 2, 3…n. Zi – реактивне зусилля  і–го зв'язку;

R_ip – вантажний член, реактивне зусилля в i–му зв'язку, викликане навантаженням. 

В матричній формі система канонічних рівнянь:         

(2.3.3)

де  R – матриця, складається з коефіцієнтів канонічних рівнянь; 

 – вектор, включає вантажні складові;

 – вектор шуканих переміщень.

Стосовно даного прикладу система канонічних рівнянь

де   r₁₁ , r₁₂, r₁₃, R_1р  – реактивні моменти, які виникають в першому додатково накладеному зв'язку від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М1=0; r₂₁ , r₂₂, r₂₃, R_2р - реактивні моменти в додатково введеному жорсткому затисненні вузла 2 від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М2=0;   r₃₁, r₃₂, r₃₃, R_3р - реактивні сили, які виникають в третьому додатково введеному зв'язку - в опорному горизонтальному стержні. Визначаються при розгляді рівноваги всіх сил на вісь додатково введеного стержня (рис. 2.3.5)  ∑Х = 0.

Реактивне зусилля в додатковому зв'язку вважається додатним, якщо напрям його дії збігається з вибраним напрямом повороту або лінійним зміщенням вузла.

(Приклад у попередньому питанні)

Змішаний метод. Ідея методу. Основні невідомі. Основна система змішаного методу. Канонічні рівняння та їх зміст. Наведіть приклад.

1. Основные теоретические положения

Смешанный метод расчета статически неопределимых систем рационально применять для рам, структура которых по длине или высоте сооружения неоднородна, т.е. в том случае, когда одна часть сооружение имеет малое количество связей, а другая, наоборот, большое количество связей и малую подвижность узлов.

В смешанном методе расчета часть неизвестных представляет собой усилия-силы (как при расчете методом сил), а другая часть – перемещения (как при расчете методом перемещений).

Рассмотрим пример:

	Таблица 1
	I часть 2 7 II часть 7 3 Итого 9 10
Рис.1.

Подсчитаем число неизвестных метода сил и метода перемещений, результат подсчета приведен в таблице 1.

Из таблицы 1 следует, что при расчете I части проще воспользоваться методом сил, а II части – методом перемещений. Таким образом число неизвестных смешанного метода равно 5, вместо 9 по методу сил и 10 по методу перемещений.

Основная система смешанного метода (ОС СМ) получена удалением связей в I части рамы и добавлением их во II части.

Рис.2.

В некоторых рамах путем удаления и наложения связей получаем такую ОС СМ, в которой имеем набор стандартных задач, а число неизвестных меньше, чем по методу сил или по методу перемещений.

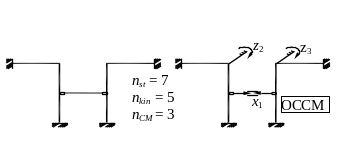
Рис.3.

Таким образом, идея смешанного метода состоит в том, что в качестве неизвестных здесь принимаются усилия в удаленных связях и перемещения тех узлов в которых добавлены связи.

Канонические уравнения смешанного метода, содержащие два типа неизвестных, будут двух видов: часть уравнений, как в методе сил, будет выражать мысль об отсутствии перемещений по направлению удаленных связей, а другая часть, как в методе перемещений, - равенство нулю реакций в добавленных в основную систему связей.

Для первого примера система канонических уравнений смешанного метода (СКУ СМ) будет иметь вид:

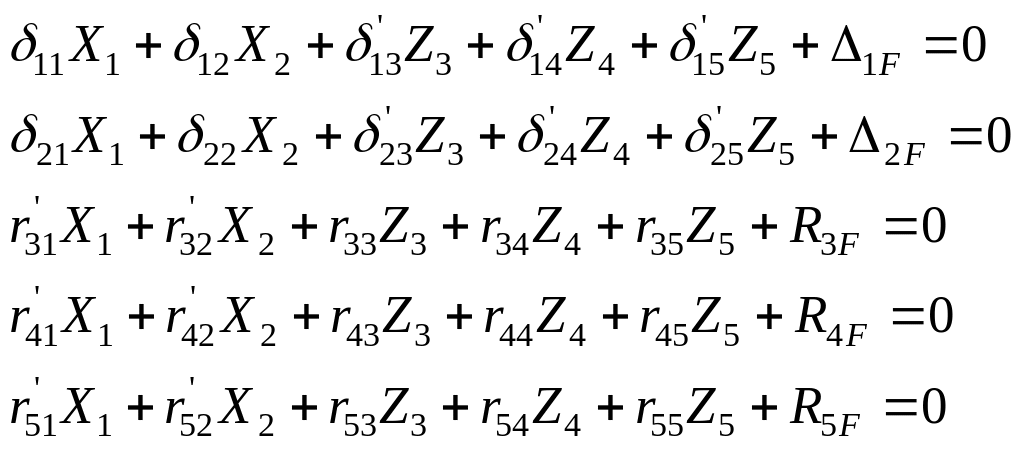
Коэффициенты СКУ СМ распадаются на четыре категории: коэффициенты метода сил ( ; ; ; ), коэффициенты метода перемещений ( ; ; ; ; ; ; ; ; ) и коэффициенты, обозначенные штрихами и представляющие собой перемещения от единичных перемещений ( ; ; ; ; ; ), реакции от действия единичных сил ( ; ; ; ; ; ).

Согласно теоремам о взаимности перемещений, реакций и реакций и перемещений между побочными коэффициентами существуют соотношения:

, , .

Решив СКУ, определяются неизвестные смешанного метода и .

Окончательная эпюра изгибающих моментов строится обычным образом по формуле:

.

Окончательную эпюру изгибающих моментов необходимо проверить и убедиться в ее правильности. Для этого необходимо провести как статическую, так и кинематическую проверки, аналогичные тем, которые выполняются в методе сил и методе перемещений