Метод переміщень. Ідея методу. Основні невідомі. Основна система методу переміщень. Канонічні рівняння та їх зміст. Наведіть приклад.

7.4 Алгоритм расчета систем методом перемещений

Расчет статически неопределимых систем методом перемещений выполняется в следующей последовательности:

1. Находим степень кинематической неопределимости заданной системы.

2. Выбираем основную систему.

3. Записываем канонические уравнения метода перемещений.

4. Строим единичные и грузовые эпюры изгибающих моментов для основной системы.

5. Определяем коэффициенты и свободные члены системы канонических уравнений.

6. Проверяем правильность вычисления коэффициентов и свободных членов системы канонических уравнений.

7. Вычисляем значения неизвестных метода перемещений.

8. Строим эпюры N, Q, M для заданной системы.

9. Проверяем правильность построения окончательных эпюр.

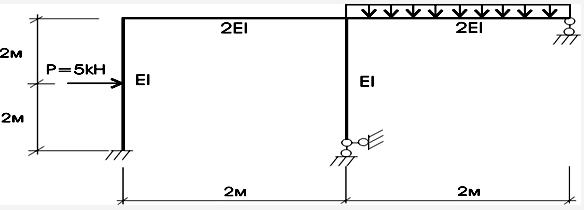
Рисунок 2.3.1 – Розрахункова схема рами

Для розрахунку рами методом переміщень необхідно визначити число невідомих кутових і лінійних переміщень (linearmoving). З цією метою підраховується число жорстких вузлів рами. Жорстким вважається вузол, в якому сходяться жорстко закріплені кінці стержнів. Число жорстких вузлів для наведеної рами  n^ж  = 2  (рис. 2.3.2).

У всі жорсткі вузли рами, включаючи опорні, вводять  шарніри. Далі досліджується  ступінь  геометричної  змінності такої модифікованої рами.

Рисунок 2.3.2 – Послідовність визначення кінематичної невизначеності при розрахунку методом переміщень: а - визначення числа жорстких вузлів; б - підрахунок числа лінійних переміщень рами

Задана рама після встановлення в неї шарнірів отримує можливість вільного переміщення по горизонталі, отже, ступінь її геометричної змінності  (degreeofgeometricalconvertibility)  nл  = I.

Ступінь кінематичної невизначеності за методом переміщень

n = nж  + nл = 2+1 = 3.

(2.3.1)

Для вибору основної системи методу переміщень в жорсткі вузли рами і за можливими напрямками лінійних зсувів вводимо додаткові зв'язки, що перешкоджатимуть кутовим і лінійним переміщенням.

Після накладання додаткових зв’язків рама перетворюється на сукупність стержнів, жорстко закріплених двома або одним кінцем. За невідомі, в основній системі методу переміщень, беремо невідомі кутові і лінійні переміщення, які виникли в додатково накладених зв'язках після прикладення навантаження.

До остаточного визначення вважаємо їх рівними одиниці.

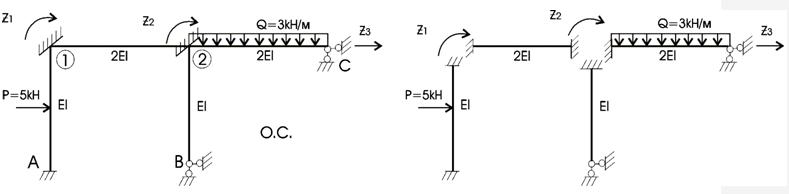
Рисунок 2.3.3 – Вибір основної системи: а - основна система методу переміщень; б - сукупність стержнів, жорстко затиснених двома або одним кінцем

Заздалегідь напрям повороту приймаємо за рухом годинникової стрілки, можливе лінійне переміщення приймаємо зміщення зліва направо.  Дійсні напрями кутових і лінійних переміщень уточнюються розрахунком.

2. Основну систему методу переміщень (рис. 2.3.3) завантажуємо по черзі кутовими і лінійними одиничними зміщеннями, а також зовнішнім навантаженням. За таблицями реактивних зусиль зігнутих стержнів будуються епюри моментів  в основній системі від одиничних вимушених переміщень і силового навантаження (рис. 2.3.4 ).

3.  Система  канонічних  рівнянь методу переміщень, яка виражає  умову рівності нулю реакцій в додаткових зв'язках, має такий вигляд:

(2.3.2)

де   – реактивне зусилля в i–му додатковому зв'язку, викликане одиничним вимушеним  переміщенням  j–го зв'язку;        i=1, 2, 3…n;     j=1, 2, 3…n. Zi – реактивне зусилля  і–го зв'язку;

R_ip – вантажний член, реактивне зусилля в i–му зв'язку, викликане навантаженням. 

В матричній формі система канонічних рівнянь:         

(2.3.3)

де  R – матриця, складається з коефіцієнтів канонічних рівнянь; 

 – вектор, включає вантажні складові;

 – вектор шуканих переміщень.

Стосовно даного прикладу система канонічних рівнянь

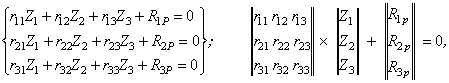
де   r₁₁ , r₁₂, r₁₃, R_1р  – реактивні моменти, які виникають в першому додатково накладеному зв'язку від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М1=0; r₂₁ , r₂₂, r₂₃, R_2р - реактивні моменти в додатково введеному жорсткому затисненні вузла 2 від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М2=0;   r₃₁, r₃₂, r₃₃, R_3р - реактивні сили, які виникають в третьому додатково введеному зв'язку - в опорному горизонтальному стержні. Визначаються при розгляді рівноваги всіх сил на вісь додатково введеного стержня (рис. 2.3.5)  ∑Х = 0.

Реактивне зусилля в додатковому зв'язку вважається додатним, якщо напрям його дії збігається з вибраним напрямом повороту або лінійним зміщенням вузла.

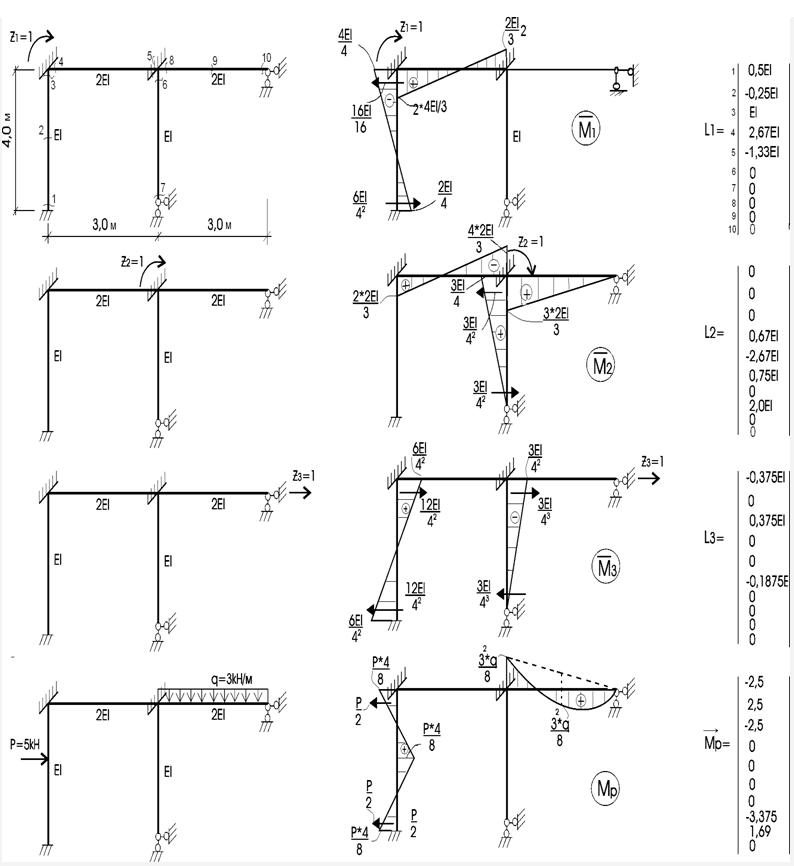
Рисунок 2.3.4 – Одиничні і вантажні епюри моментів в основній системі методу переміщень. Матриці впливу одиничних переміщень по характерних перетинах