77 Ймовірність попадання в мішень при одному пострілі рівна 3/8. Яка ймовірність того, що при шести пострілах буде хоча б два попадання?

в) 0,726;

Подія є протилежною тій, коли буде 0 або 1 попадання. Використуємо формулу Бернуллі.

78 Подія настає тоді, коли подія настане не менше чотирьох разів. Знайти ймовірність настання події , якщо здійснюється 5 незалежних випробувань, у кожному з яких імовірність настання події дорівнює 0,8.

а) 0,737; Використаємо формулу Бернуллі.

79 Випадковий перехожий з імовірністю 0,2 може бути брюнетом, з імовірністю 0,3 – шатеном, з імовірністю 0,4 – блондином і з ймовірністю 0,1 – рудим. Яка ймовірність того, що серед шести випадково зустрінутих людей не менше чотирьох блондинів? г) 0,1792

Тобто прийнятними є виранти, коли 4,5 або 6 блондинів. Використаємо формулу Бернуллі.

80 Яка ймовірність того, що при п’яти підкиданнях монети хоча б 2 рази випаде герб? б) 0,8125;

Дана подія є протилежною тій, коли герб випаде менше 2 разів. Використаємо формулу Бернуллі.

81 Яка ймовірність, що серед 200-т чоловік буде не менше чотири лівші, якщо вони в середньому складають 1% від загальної кількості людей?

д) інша відповідь.

82 Підручник надруковано тиражем 5000 примірників. Ймовірність того, що підручник буде бракованим дорівнює 0,001. Знайти ймовірність того, що тираж має не більше трьох бракованих підручників. г) ;

Використаємо формулу Бернуллі, а також теореми множення і додавання ймовірностей.

Для даної події прийнятними є випадки, коли тираж містить 0, 1, 2 або 3 браковані підручники.

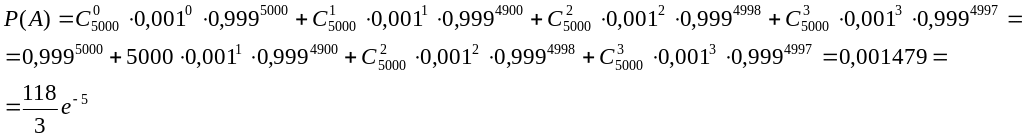
83 Завод відправив на базу 10000 доброякісних виробів. Ймовірність пошкодження кожного виробу під час транспортування на базу дорівнює 0,0001. Знайти ймовірність того, що під час транспортування буде пошкоджено не більше, як 3 вироби. б) ;

Використаємо формулу Бернуллі, а також теореми множення і додавання ймовірностей.

Для даної події прийнятними є випадки, коли тираж містить 0, 1, 2 або 3 браковані вироби.

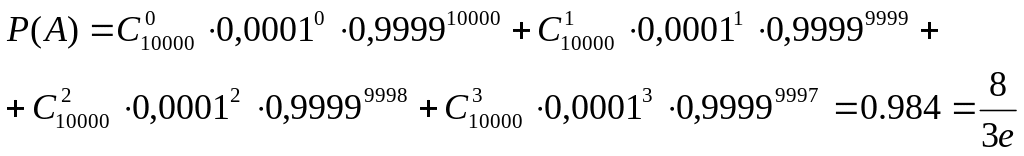
84 Ймовірність того, що виріб має дефект дорівнює 0,005. знайти ймовірність того, що в партії із 600 виробів з дефектом будуть менше трьох виробів. в) ;

Використаємо формулу Бернуллі, а також теореми множення і додавання ймовірностей.

Для даної події прийнятними є випадки, коли тираж містить 0, 1, 2 браковані вироби.

85 ймовірність пошкодження виробу при транспортуванні дорівнює 0,002. Знайти ймовірність того, що при транспортуванні 2000 виробів буде пошкоджено більше, ніж 2 вироби. а) ;

Використаємо формулу Бернуллі, а також теореми множення і додавання ймовірностей.

Дана подія є протилежною тій, при якій буде пошкоджено 0, 1 або 2 вироби.

86 Ймовірність несплати податку для кожного із 400 підприємств дорівнює 0,1. Яка найімовірніша кількість підприємств, що не сплатять податки?

г) 40;

87 Ймовірність того, що виріб вищого сорту дорівнює 0,25. Яка найімовірніша кількість виробів вищого сорту в партії із 350 виробів?

б) 87;

88 За даними відділу технічного контролю серед виготовлених деталей у середньому 1,5% браку. Знайти найімовірнішу кількість бракованих деталей у партії із 300 деталей. в) 4;

89 Ймовірність влучання в мішень під час одного пострілу дорівнює 0,6. Яку найменшу кількість пострілів потрібно виконати, щоб найімовірніша кількість влучань у мішень дорівнювала 25? в) 41;

90 Ймовірність настання події в одному випробуванні дорівнює 0,3. Яку найменшу кількість незалежних випробувань потрібно провести, щоб найімовірніша кількість настання події в цих випробуваннях дорівнювала 20? б) 66;

91 Дискретна випадкова величина задана законом розподілу:

	1	3	6
P	0,2	0,5	0,3

Знайти функцію розподілу.

б) ; Б .

92 Влучення при окремих пострілах - незалежні події з ймовірністю 2/3. - кількість влучень при трьох пострілах. Знайти закон розподілу випадкової величини . д) інша відповідь.

В .

_=0:

_=1:

_=2:

_=3:

в)		0	1	2	3

93 Задано закон розподілу дискретної випадкової величини . Знайти .

	-4	-1	2	5	8	10
p		1,5	0,5	3,5	2,5

б) 0,1;

Для того, щоби дана таблиця була законом розподілу, треба, щоби , тобто: а+1,5а+0,5а+3,5а+2,5а+а=10а=1 а=0,1