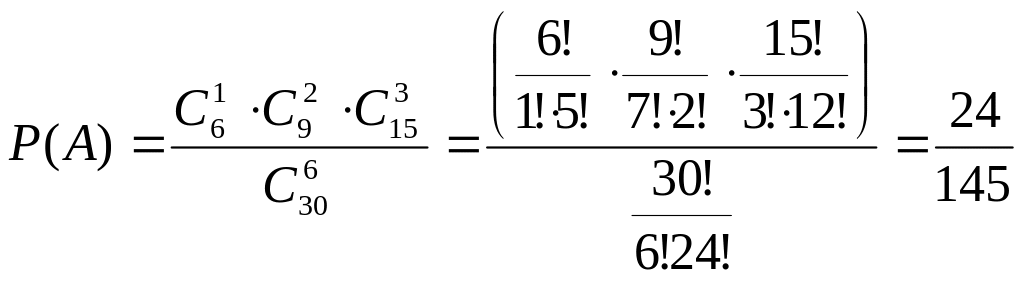рівень C

1 Задано множину чисел {1,2,3,4,5}. Числа навмання розміщують в рядок. Яка ймовірність того, що при цьому утвориться парне п'ятицифрове число? а) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

Використавши метод безпосереднього підрахунку ймовірностей, а також теормеми множення і додавання ймовірностей, маємо:

2 У групі 15 студентів, серед яких 8 відмінників. Навмання вибрано 9 студентів. Знайти ймовірність того, що серед вибраних студентів буде 6 відмінників. б) 0,196

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

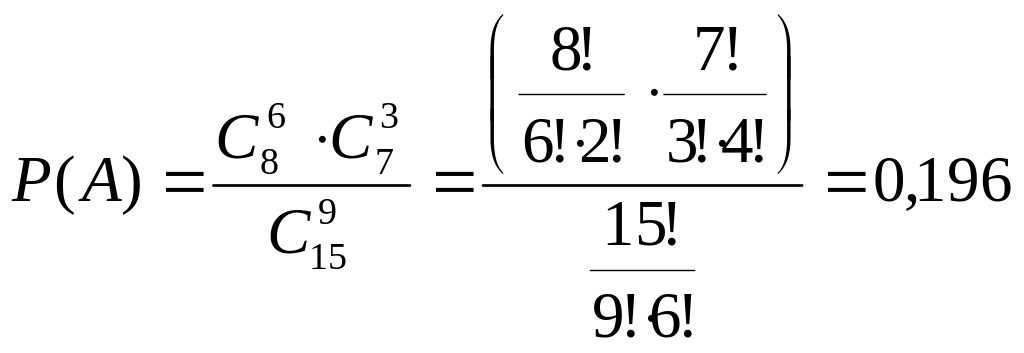
3 Переможцями конкурсу стали 3 жінок та 4 чоловіків. Організатори випадковим чином обрали 4 особи для вручення суперпризів. Яка ймовірність того, що серед них буде дві жінки і два чоловіка? в) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

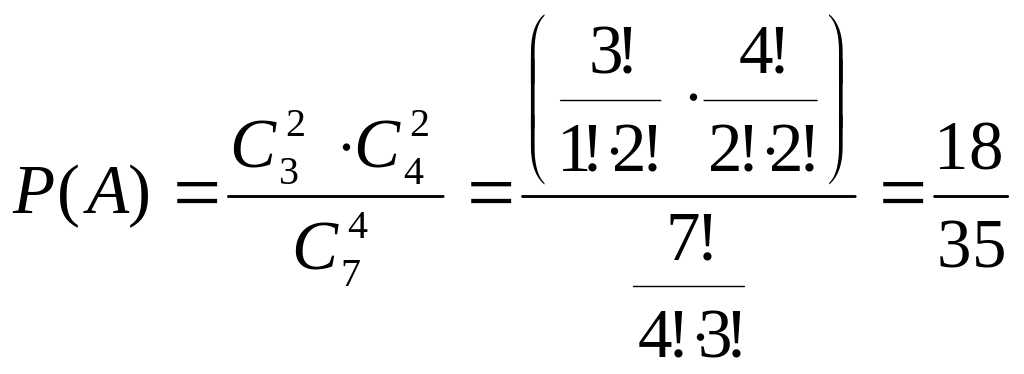
4 В аудиторії серед 15 комп'ютерів 12 справних. Знайти ймовірність того, що з двох вибраних комп'ютерів хоча б один виявиться несправним.Г) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Дана подія є протилежною до події, коли два з двох комп’ютерів будуть несправні.

5 Один раз підкидають три гральних кубики. Яка ймовірність того, що на різних кубиках випаде різна кількість очок? б) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Використавши метод безпосереднього підрахунку ймовірностей, а також теормеми множення і додавання ймовірностей, маємо:

6 Один раз підкидають три гральних кубики. Яка ймовірність того, що на всіх кубиках випаде однакова кількість очок? г) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Використавши метод безпосереднього підрахунку ймовірностей, а також теореми множення і додавання ймовірностей, маємо:

7 Один раз підкидають три гральних кубики. Яка ймовірність того, що хоча б на двох кубиках випаде однакова кількість очок? в) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

Дана подія є протилежною до події, коли на всіх трьох кубиках будуть різна кількість очок:

8 Серед 20 ламп 5 бракованих. Знайти ймовірність того, що із чотирьох взятих навмання ламп всі будуть доброякісні. б) 0,282;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Використавши метод безпосереднього підрахунку ймовірностей, а також теореми множення і додавання ймовірностей, маємо:

9 Серед 20 ламп 5 бракованих. Навмання взято 4 лампи. Яка ймовірність того, що серед взятих буде хоча б одна бракована? д) інша відповідь.

Дана подія є протилежною до випаду, коли немає жодної бракованої лампи. Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Використавши метод безпосереднього підрахунку ймовірностей, а також теореми множення і додавання ймовірностей, маємо:

10 12 осіб шикуються в шеренгу довільним чином. Знайти ймовірність того, що дві певні особи будуть стояти поруч. а) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

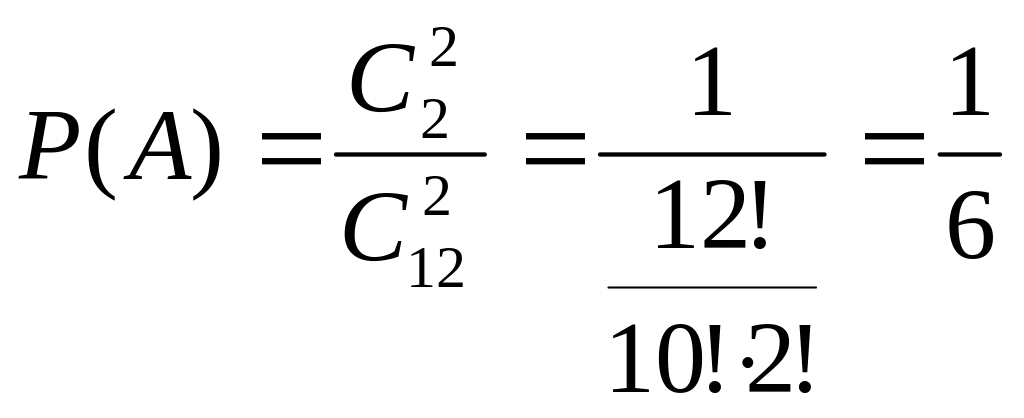
11 Номер випадково взятого автомобіля чотирицифровий. Знайти ймовірність того, що номер не містить однакових цифр. в) 0,504;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій. Використавши метод безпосереднього підрахунку ймовірностей, а також теореми множення і додавання ймовірностей, маємо:

12 Номер випадково взятого автомобіля чотирицифровий. Знайти ймовірність того, що номер містить дві однакові цифри. б) 0,432;

13 В урні є 12 кульок, з них 8 червоних і 4 чорних. Навмання вибирають 6 кульок. Яка ймовірність того, що вибрано дві чорних кульки? г) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

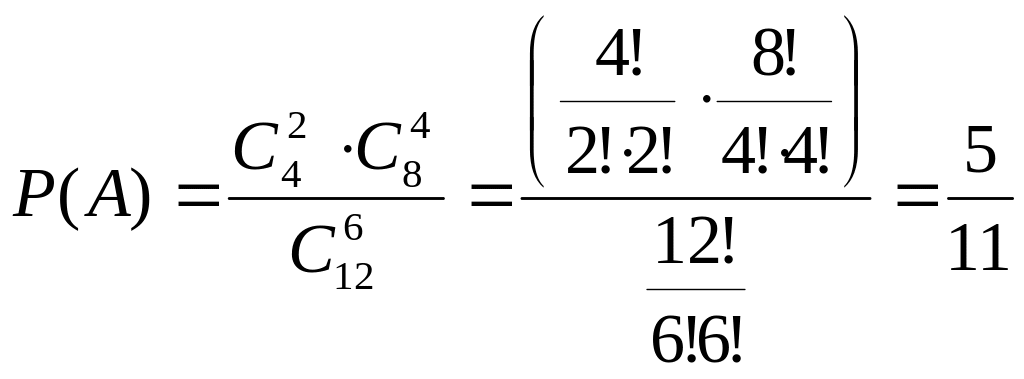
14 В урні є 12 кульок, з них 8 червоних і 4 чорних. Навмання вибирають 6 кульок. Яка ймовірність того, що вибрано хоча б одну чорну кульку?г) ;

Дана подія є протилежною до події, коли обидві вибраних кульки червоні. Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.

15 В урні є 15 червоних, 9 синіх та 6 зелених кульок. Навмання вибирають 6 кульок. Знайти ймовірність того, що буде вийнято 1 зелену, 2 синіх і 3 червоних кульки? в) ;

Використаємо класичне означення ймовірностей: , де - число подій, сприятливих появі заданої події, - число всіх можливих подій.